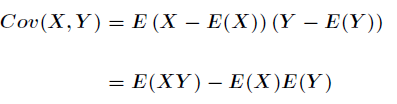协方差专题

CV-CNN-2015：GoogleNet-V2【首次提出Batch Norm方法：每次先对input数据进行归一化，再送入下层神经网络输入层（解决了协方差偏移问题）】【小的卷积核代替掉大的卷积核】

GoogLeNet凭借其优秀的表现，得到了很多研究人员的学习和使用，因此GoogLeNet团队又对其进行了进一步地发掘改进，产生了升级版本的GoogLeNet。 GoogLeNet设计的初衷就是要又准又快，而如果只是单纯的堆叠网络虽然可以提高准确率，但是会导致计算效率有明显的下降，所以如何在不增加过多计算量的同时提高网络的表达能力就成为了一个问题。 Inception V2版本的解决方案就是修

平均值，标准差，方差，协方差，期望，均方误差

1. 写在前面平均值，标准差，方差，协方差都属于统计数学；期望属于概率数学。 2. 统计数学 2.1 平均值，标准差，方差统计学里最基本的概念就是样本的均值、方差、标准差。首先，我们给定一个含有n个样本的集合，下面给出这些概念的公式描述：均值：方差：标准差：均值描述的是样本集合的中间点，它告诉我们的信息是有限的。方差（variance)是在概率论和统计方差衡量随机变

协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系

协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系文章目录协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系引言协方差的概念与背景数学公式推导实例背景数据收集计算过程结果解释计算相关系数为什么使用协方差？结论商业启示引言在日常生活中，我们经常会遇到需要分析两个变量之间关系的情况。其中一个重要的统计量就是协方差，它可以帮助我们理解

基于协方差信息的Massive MIMO信道估计算法性能研究

1. 引言随着移动互联网不断发展，人们对通信的速率和可靠性的要求越来越高[1]。目前第四代移动通信系统已经逐渐商用，研究人员开始着手研究下一代移动通信系统相关技术[2][3]。在下一代移动通信系统中要求下行速率达到10Gbps，这就要求我们使用更先进的技术和更宽的系统带宽。MIMO技术由于可以在不增加系统带宽和功率的前提下，成倍的提升系统容量和可靠性，已经广泛应用于各种无线通信系统中，但仅采用

MATLAB算法实战应用案例精讲-【数模应用】协方差分析

目录前言算法原理什么是协方差协方差分析的基本思想协方差分析的理论假设协方差分析的数学模型协方差分析的基本假定编辑协方差分析的步骤算法步骤 SPSSAU 协方差分析 1、背景 2、理论 3、操作 4、SPSSAU输出结果 5、文字分析 6、剖析疑难解惑均方平方和类型？事后多重比较的类型选择说明？事后多重比较与‘单独进行事后多重

椭圆的标准方程与协方差矩阵的特征值和特征向量的关系

椭圆的标准方程与协方差矩阵的特征值和特征向量的关系 flyfish 单位圆：单位圆表示在标准正交基下的分布。椭圆：通过协方差矩阵的特征向量和特征值变换得到的椭圆，表示数据在新的坐标系下的分布。特征向量：红色箭头表示特征向量方向，即椭圆的主要轴方向。特征值：红色箭头的长度表示特征值大小，即椭圆沿主要轴的伸缩程度。 import numpy as npimport ma

【数学与算法】协方差矩阵与 w*w^T 的关系

下面的二维向量 W ⃗ \vec W W 只是一个样本，对于多个样本才能谈论协方差，因为协方差和方差是求一系列样本的协方差和方差，单个样本并没有协方差这一说。下面公式中的求 w 1 w1 w1的期望和方差，是求所有样本的 w 1 \displaystyle\color{blue}w1 w1特征的期望和方差。不过下面的 W ⃗ W ⃗ T \displaystyle\color{blue

协方差和协方差矩阵简要概述

在统计学中，我们见过的最基本的三个概念是均值，方差，标准差。假定给定了n个样本的集合，那么公式如下均值是描述样本的平均值，标准差描述的是样本集合的各个点到均值距离的平均，体现了样本的散步程度。而方差仅仅是标准差的平方。实际上，上述的方差是针对一维数据的情况进行统计描述。考虑这样一种情况：假设我们需要对两个集合的数据进

DeepSORT（目标跟踪算法）中的初始化卡尔曼滤波器的状态向量和协方差矩阵

DeepSORT（目标跟踪算法）中的初始化卡尔曼滤波器的状态向量和协方差矩阵 flyfish 如果看了下面遇到了状态转移矩阵，可以先看 DeepSORT（目标跟踪算法）中的卡尔曼滤波 - 看了就会的状态转移矩阵，这里做了非常详细的描述 import numpy as npnp.set_printoptions(suppress=True)class KalmanFilter(object)

从零开始学统计 04 | 协方差与相关性分析

一、老板的任务老板今天又给一个任务：计算肝脏细胞中 X 基因与 Y 基因的关系。现在，两个基因在各个细胞中的表达值都有了。绘制不同细胞中 X，Y 基因的表达值在坐标轴上。计算 X 基因和 Y 基因在5个细胞中的均值，标准差。因为这些测量值都是来自同一个细胞，所以我们可以成对来看：那么这样成对的测量可以告诉我们哪些信息呢？现在，先将一对细胞连接，绘制一个点

【NumPy】深入理解NumPy的cov函数：计算协方差矩阵的完整指南

🧑 博主简介：阿里巴巴嵌入式技术专家，深耕嵌入式+人工智能领域，具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍：分享嵌入式开发领域的相关知识、经验、思考和感悟，欢迎关注。提供嵌入式方向的学习指导、简历面试辅导、技术架构设计优化、开发外包等服务，有需要可加文末联系方式联系。 💬 博主粉丝群介绍：① 群内高中生、本科生、研究生、博士生遍布，可互相学习，交流困惑。② 热榜t

协方差和相关系数的概念和含义

1.协方差：　　在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：当 X, Y 的联合分布像上图那样时，我们可以看出，大致上有： X 越大 Y 也越大， X 越小 Y 也越小，这种情况，我们称为“正相关”。当X, Y 的联合分布像上图那样时，我们可以看出，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为“负相关”。

图像算法的基础知识(双线性插值，协方差矩阵，矩阵的特征值、特征向量）

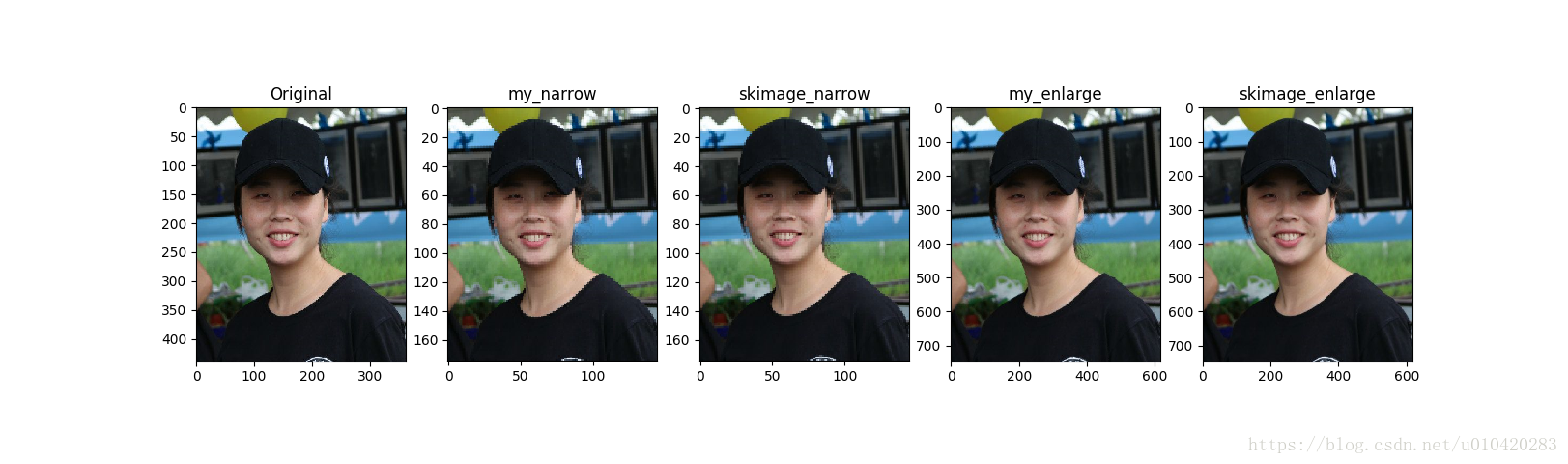
0. 前言 MATLAB或者OpenCV里有很多封装好的函数，我们可以使用一行代码直接调用并得到处理结果。然而当问到具体是怎么实现的时候，却总是一脸懵逼，答不上来。前两天参加一个算法工程师的笔试题，其中就考到了这几点，感到非常汗颜！赶紧补习！ 1. 双线性插值在图像处理中，我们有时需要改变图像的尺寸，放大或者缩小。线性插值则是这类操作的关键算法。不管是放大还是缩小操作，其实都是一个像素映射

稀疏表示学习笔记--正交阵，协方差

自己的数学基础比较差，特别是矩阵一块，有一些名词看到了可能不能立刻反应出是什么意思，所以在这里进行一些记录。 1、正交矩阵如果：AA T=E（E为单位矩阵，A T表示“矩阵A的转置矩阵”。）或A TA=E，则n阶实矩阵A称为正交矩阵，若A为正交阵，则满足以下条件: 1) A T是正交矩阵 2) （E为单位矩阵） 3) A的各行是单位向量且两两正交 4) A

数据分析的几个数值P值、T值和R值（相关系数）中位数、众数、方差、标准差、协方差、置信区间

统计学中包含了多个基本概念和数值，以下是关于P值、T值和R值（相关系数）的简要解释，以及其他一些常见的统计学数值： P值（P value）： P值是用来判定假设检验结果的一个参数。它表示在原假设为真时，比所得到的样本观察结果更极端的结果出现的概率。如果P值很小，说明原假设情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设。P值越小，拒绝原假设的理由越充分。 T值（T-

AI笔记: 数学基础之数字特征-标准差、协方差、相关系数、中心矩、原点矩、峰度、偏度

标准差标准差(Standard Deviation)是离均值平方的算术平均数的平方根，用符号 σ \sigma σ 表示，其实标准差就是方差的算术平方根标准差和方差都是测量离散趋势的最重要、最常见的指标。标准差和方差的不同点自傲与，标准差和变量的计算单位是相同的，比方差清楚，因此在很多分析的时候使用的是标准差 σ = D ( X )

数据可视化（七）：Pandas香港酒店数据高级分析，涉及相关系数，协方差，数据离散化，透视表等精美可视化展示

Tips："分享是快乐的源泉💧，在我的博客里，不仅有知识的海洋🌊，还有满满的正能量加持💪，快来和我一起分享这份快乐吧😊！喜欢我的博客的话，记得点个红心❤️和小关小注哦！您的支持是我创作的动力！数据源存放在我的资源下载区啦！数据可视化（七）：Pandas香港酒店数据高级分析，涉及相关系数，协方差，数据离散化，透视表等精美可视化展示目录数据可视化（七）：Pandas香

协方差和协相关(Covariance and Correlation)

本文主要是记录与这两个概念相关的概念。看中文或者英文时，尝尝容易弄混。内容 1 covariance和correleation2 covariance matrix和correlation matrix3 cross-covariance和cross-correlation4 autocovariance和autocorrelation 对于两个随机信号X, Y 1 cova

协方差(covariance)和相关系数(correlation coefficient)

相关系数和协方差实际上是相同的概念，都是用来描述两个随机变量之间的相似程度的。这篇文章将详细说明协方差和相关系数的相关知识。首先声明，此篇的内容是来自"马同学高等数学"微信公众号的内容。 1、事物之间的关系事物之间有两种关系，有关系和没关系。 1.1 、有关系据专家表示，要买房的人越多（下图的城镇化率可以简单理解为进城买房的人数），房价就越高（数据来源）：

【概率论】4-6:协方差和相关性(Covariance and Correlation)

原文地址1：https://www.face2ai.com/Math-Probability-4-6-Covariance-and-Correlation转载请标明出处 Abstract: 本文介绍协方差和相关性的基础知识，以及部分性质 Keywords: Covariance,Correlation,Properties of Covariance and Correlation 协方差和相关

数学期望，方差，标准差，样本方差，协方差，相关系数概念扫盲

数学期望在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。再举个例子理解一下数学期望：方差概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏

求两个向量的协方差

根据D（A＋B）＝D（A）＋D（B）+2COV（A，B）计算 private double GetConv(double[] a, double[] b){if (a.Length != b.Length){return 0;//error}double cov = 0;double meana = 0;double meanb = 0;double meanab = 0;double de

MATLAB 构建协方差矩阵，解算特征值和特征向量（63）

MATLAB 局部点云构建协方差矩阵，解算特征值和特征向量（63）一、算法介绍二、算法实现1.代码2.结果一、算法介绍对于某片有待分析的点云，我们希望构建协方差矩阵，计算特征值和特征向量，这是很多算法必要的分析方法，这里提供完整的计算代码（验证正确） !!! 特别需要注意的是：特征值的排序方式这里计算的特征值按照从小到大的顺序重新排列得到：L1 > L2 >

协方差矩阵（转）

https://blog.csdn.net/shenziheng1/article/details/52955687

协方差的理解

1. 协方差的意义：协方差的定义，两个变量总体误差的期望：定理：数据0中心化后， (X * X转置) /n 等于协方差矩阵解决多维样本之间的特征联系：协方差矩阵：可见：协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。 ①协方差就是看两个变量是否正负相关，也就是数值上变化是否同或反向； ②相关系数直接衡量的就是线性相关关系，取值就在+-1之间，体现的含

$excel统计分析——协方差分析的作用$

excel统计分析——协方差分析的作用

参考资料：生物统计学 1、协变量与试验因素的区别如果把协方差分析资料中的协变量看作多因素方差分析资料中的一个因素，则两类资料有相似之处，但两类资料有本质的不同。在方差分析中，各因素的水平时人为控制的，即使是随机因素也是认为选定的；而在协方差分析中，协变量不能人为控制。例如，当考虑动物窝别对增重的影响时，一般可以把窝别当作随机因素，将不同窝看作不同水平，进行