图像算法的基础知识(双线性插值，协方差矩阵，矩阵的特征值、特征向量）

本文主要是介绍图像算法的基础知识(双线性插值，协方差矩阵，矩阵的特征值、特征向量），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 前言

MATLAB或者OpenCV里有很多封装好的函数，我们可以使用一行代码直接调用并得到处理结果。然而当问到具体是怎么实现的时候，却总是一脸懵逼，答不上来。前两天参加一个算法工程师的笔试题，其中就考到了这几点，感到非常汗颜！赶紧补习！

1. 双线性插值

在图像处理中，我们有时需要改变图像的尺寸，放大或者缩小。线性插值则是这类操作的关键算法。不管是放大还是缩小操作，其实都是一个像素映射的处理。如下图从小图到大图的映射，以及从大图到小图的映射。

图像来源：https://www.cnblogs.com/sdxk/p/4056223.html

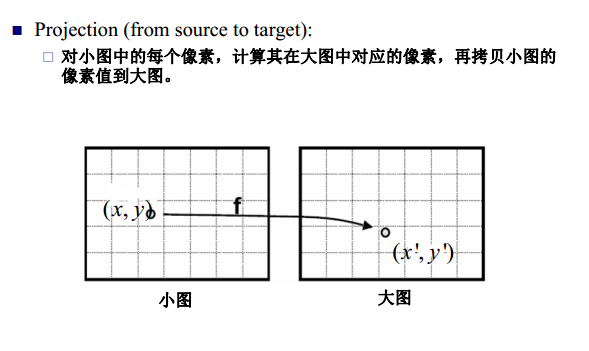
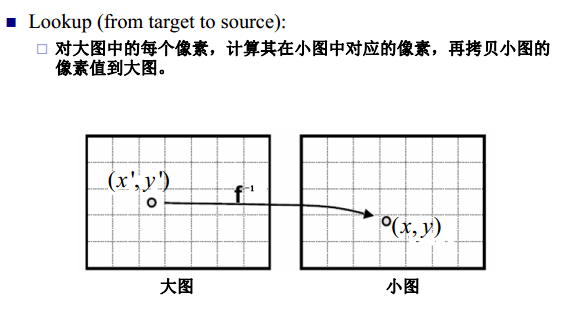
然而，这两种操作都有一定的缺点。对于把小图放大的操作，因为小图中的像素点到大图中的像素点不是满射，因此大图中的点不能完全有像素值；对于将大图缩小的操作，大图中的点逆映射为小图中的点时，得到的像素坐标值可能不是整数。一种解决办法是采用最近邻方法，即将得到的坐标值与相邻的原图像中的像素坐标值比较，取离得最近的坐标值对应的像素值作为缩放后的图像对应的坐标值的像素值，但是这种办法可能导致图像失真，因此可以采用双线性差值的办法来进行计算相应的像素值。

对于图中红色的四个点（Q11,Q12,Q21,Q22）为源图像中存在的点，需要求在目标图像的插值（绿色点P）的坐标对应的像素值。

首先在X轴进行插值，R1，R2是两个插值过程中过渡的点.

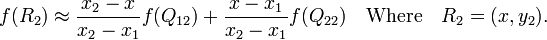
然后在 y 方向进行线性插值，得到：

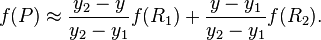
这样就得到所要的结果 $f \left( x, y \right)$ ,

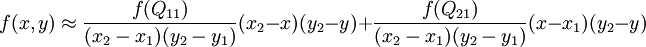
讲一个具体的例子：

比如源图像是尺寸是（100,150），现在要缩小尺寸0.6倍，即目标图像的尺寸是（60,90），则求目标图像在坐标为P[10,4]的点的像素值怎么求呢？

假设源图像是ori_im，目标图像是tar_im，tra_im[10,4]表示在行列分别是10和4时候图像的像素值。

此时，x=10/0.6=16.67, y=4/0.6=6.67，而x1=16,x2=17,y1=6,y2=7, (x1,y1), (x1,y2), (x2,y1), (x2,y2)是在源图像中最接近tra_im[10,4]的4个点。

tra_im[10,4]=ori_im[x1,y1]*(17-16.67）*（7-6.67）+ori_im[x2,y1]*(16.67-16）*（6.67-6）+ori_im[x2,y1]*(17-16.67）*（6.67-6）+ori_im[x2,y2]*(16.67-16）*（6.67-6）

带入4个点在源图像中对应的像素值即可得到缩小后图像的像素值。

下面我用python实现了这个双线性插值，并和python中自带的skimage函数里封装的resize进行了效果对比，感觉效果差不多。（代码可能有点冗余）

我的代码：

# -*- coding: utf-8 -*-
# Author: lmh
# Time: 2018.10.22
from skimage import transform
import matplotlib.pyplot as plt
import matplotlib.image as mping
import numpy as np
def chazhi(x,y,im)：
#x,y分别是缩放或者放大后对应源图像的浮点坐标位置，im是源图像，返回目标图像根据插值计算得到的像素值x1,y1=int(x),int(y) #x1,x2,x3,x4分别是插值坐标对应在源图像上下左右最近的点的坐标x2,y2=x1+1,y1+1pixel11,pixel21,pixel12,pixel22=im[x1-1,y1-1],im[x2-1,y1-1],im[x2-1,y1-1],im[x2-1,y2-1]#以下是根据双线性插值的公式求得的目标图像的该位置的像素值new_pixel=(x2-x)*(y2-y)*pixel11+(x-x1)*(y2-y)*pixel21+(x2-x)*(y-y1)*pixel12+(x-x1)*(y-y1)*pixel22return new_pixelim=mping.imread('C:\\Users\\shou\\Desktop\\photo.png')
im11=im
scale=0.4 #缩小程度
row,col=int(im.shape[0]*scale),int(im.shape[1]*scale)
im_sml=np.zeros([row,col,3])
for k in range(3):im1 = im[:, :, k]for i in range(row):for j in range(col):value=chazhi(i/scale,j/scale,im1)#3通道图像逐像素计算缩小或者放大后的新像素值im_sml[i][j][k]=valueim_narrow=im_smlscale=1.7  #扩大程度
row, col = int(im.shape[0] * scale), int(im.shape[1] * scale)
im_sml = np.zeros([row, col, 3])
for k in range(3):im1 = im[:, :, k]for i in range(row):for j in range(col):value = chazhi(i / scale, j / scale, im1)im_sml[i][j][k] = valueim_enlarge=im_sml
python_narrow=transform.resize(im, (175, 145)) #使用skimage自带函数resize图像，也可以直接写像上面一样写比例（0.4,1.7）
python_enlarge=transform.resize(im, (746, 617))#为了对比，两种方法特意放大和缩小一样大小plt.figure()
plt.subplot(151)
plt.imshow(im11,plt.cm.gray)
plt.title('Original')
# plt.axis('off')plt.subplot(152)
plt.imshow(im_narrow,plt.cm.gray)
plt.title('my_narrow')
# plt.axis('off')plt.subplot(153)
plt.imshow(python_narrow,plt.cm.gray)
plt.title('skimage_narrow')
# plt.axis('off')plt.subplot(154)
plt.imshow(im_enlarge,plt.cm.gray)
plt.title('my_enlarge')
# plt.axis('off')plt.subplot(1,5,5)
plt.imshow(python_enlarge,plt.cm.gray)
plt.title('skimage_enlarge')
# plt.axis('off')
plt.savefig('image_comp.png')

skimage的源码：

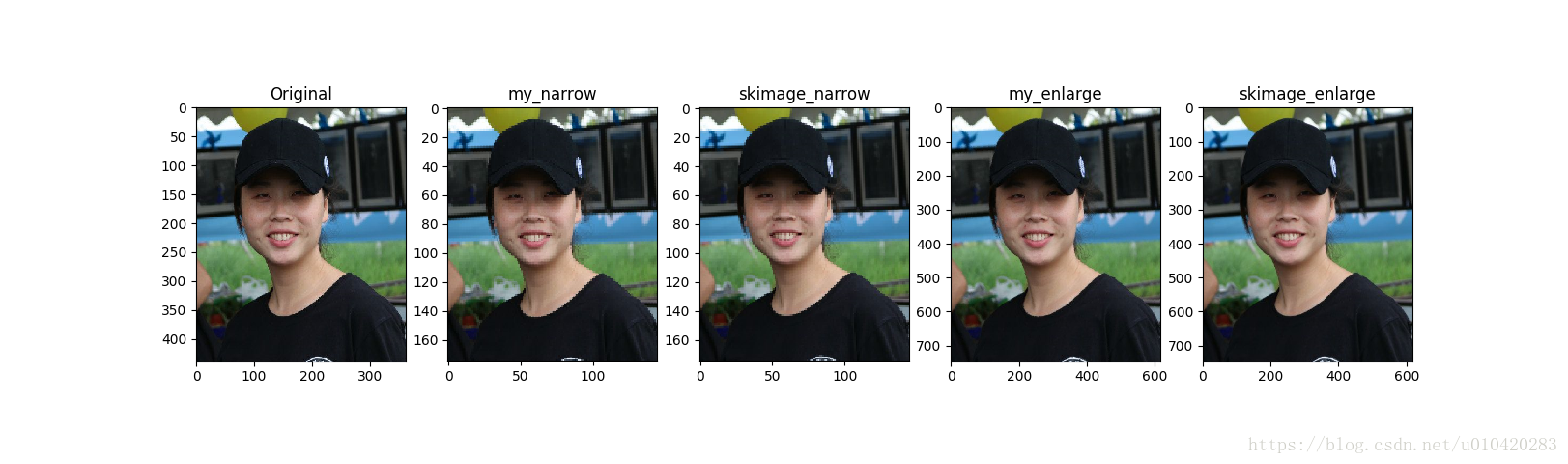
效果图对比（原图[439,363,3]；缩小0.4倍后为[175,145,3]；放大1.7倍后为[746,617,3]）

在博客：https://www.cnblogs.com/sdxk/p/4056223.html中，博主讲根据双线性插值的定义，我们自己写的函数图像处理的结果会因为坐标系的原因，而和MATLAB，OpenCV结果的完全不同。最好的解决方法就是，两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距，这也是matlab和openCV的做法。并给出了以下解决方法，其中m,n 是源图像尺寸；a,b是目标函数尺寸。然而我没有这些修改，与python封装的方法也没发现太大区别。

int x=(i+0.5)*m/a-0.5

int y=(j+0.5)*n/b-0.5

代替

int x=i*m/a

int y=j*n/b

补：经过查看Skimge的resize源码,发现确实里面添加了上面所说的策略（下面的代码），那么为什么我写的双线性代码没有这样做，图像的结果确和这样做的几乎一样？更加疑惑了

# take into account that 0th pixel is at position (0.5, 0.5)
dst_corners[:, 0] = col_scale * (src_corners[:, 0] + 0.5) - 0.5
dst_corners[:, 1] = row_scale * (src_corners[:, 1] + 0.5) - 0.5