特征向量专题
线性代数 第六讲 特征值和特征向量_相似对角化_实对称矩阵_重点题型总结详细解析
文章目录 1.特征值和特征向量1.1 特征值和特征向量的定义1.2 特征值和特征向量的求法1.3 特征值特征向量的主要结论 2.相似2.1 相似的定义2.2 相似的性质2.3 相似的结论 3.相似对角化4.实对称矩阵4.1 实对称矩阵的基本性质4.2 施密特正交化 5.重难点题型总结5.1 判断矩阵能否相似对角化5.2 已知两个矩阵相似,求某个矩阵中的未知参数5.3 相似时,求可逆矩阵P,使
处理特征向量和离散特征
在最新的腾讯的社交广告大赛中,数据如下,如何处理这种向量的特征 比如intersets1,interests2.... LBS,950,age,4,carrier,1,consumptionAbility,2,ct,3 1,education,7,gender,2,interest1,93 70 77 86 109 47 75 69 45 8 29 49 83 6 46 36
MATLAB eig 函数简介:计算特征值和特征向量
在数据科学、工程学和数学中,特征值和特征向量是理解和分析矩阵行为的核心概念。MATLAB 的 eig 函数是处理这些概念的强大工具。本文将介绍 eig 函数的基本用法,并通过示例展示如何使用它来计算特征值和特征向量。 什么是特征值和特征向量? 在矩阵分析中,特征值和特征向量帮助我们理解一个矩阵的性质。例如,在物理学中,它们可以用来描述系统的稳定性;在机器学习中,它们被用于数据降维和特征提取。
矩阵的特征值和特征向量的雅克比算法C/C++实现
矩阵的特征值和特征向量是线性代数以及矩阵论中非常重要的一个概念。在遥感领域也是经常用到,比如多光谱以及高光谱图像的主成分分析要求解波段间协方差矩阵或者相关系数矩阵的特征值和特征向量。 根据普通线性代数中的概念,特征值和特征向量可以用传统的方法求得,但是实际项目中一般都是用数值分析的方法来计算,这里介绍一下雅可比迭代法求解特征值和特征向量。 雅克比方法用于求实对称阵的全部特征值、特征向量。 对
线性代数|机器学习-P32循环矩阵的特征向量-傅里叶矩阵
文章目录 1. 大纲2. 循环矩阵2.1 移位矩阵P2.2 P的特征值和特征向量2.3 循环卷积矩阵2.4 循环卷积计算 3. 傅里叶矩阵 1. 大纲 循环矩阵在机器学习,图像处理中的应用循环卷积矩阵的特征值,特征向量,卷积规则循环卷积矩阵多项式表达: C = c 0 I + c 1 P + c 2 P 2 + ⋯ + c n − 1 P n − 1 C=c_0 I+c_1P+c
字符串的特征向量与KMP算法
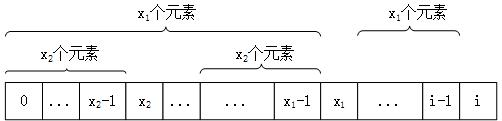
字符串的特征向量就是由字符串各位置上的特征数构成的一个向量。设字符串为P,令Pi为从字符串首字母到第i个位置的前缀,则字符串P的i位置上的特征数就是Pi的首尾非空真子串匹配的最大长度。例如:字符串abcdaabcab的特征向量是(0,0,0,0,1,1,2,3,1,2)。其中第5个位置的特征数是1,因为P5是abcdaa,首尾非空真子串能够匹配的就是a;而第7个位置的特征数是3,因为P7是abcd
特征值和特征向量的几何意义、计算及其性质
http://www.cnblogs.com/chaosimple/p/3179695.html 一、特征值和特征向量的几何意义 特征值和特征向量确实有很明确的几何意义,矩阵(既然讨论特征向量的问题,当然是方阵,这里不讨论广义特征向量的概念,就是一般的特征向量)乘以一个向量的结果仍是同维数的一个向量。因此,矩阵乘法对应了一个变换,把一个向量变成同维数的另一个向量。 那么变换的效果是
椭圆的标准方程与协方差矩阵的特征值和特征向量的关系
椭圆的标准方程与协方差矩阵的特征值和特征向量的关系 flyfish 单位圆 :单位圆表示在标准正交基下的分布。 椭圆 :通过协方差矩阵的特征向量和特征值变换得到的椭圆,表示数据在新的坐标系下的分布。 特征向量 :红色箭头表示特征向量方向,即椭圆的主要轴方向。 特征值 :红色箭头的长度表示特征值大小,即椭圆沿主要轴的伸缩程度。 import numpy as npimport ma
矩阵理论基础知识(1)--特征值与特征向量
之所以想起来总结这部分的知识,也是由于目前学习的机器学习算法中,矩阵论/矩阵分析呈刷屏似的出现,而之前本科阶段的高等代数中,总是只知道有这么个东西,也初略知道怎么计算,但不知道其中的真正含义,因此这两天决定将这块知识汇总下,知其然也知其所以然。 首先介绍几个基本的概念: 向量组线性无关:向量组中的任何一个向量都不能被其它向量线性表出。即当且仅当k1=k2…=kr=0时,k1α1+k2α2+…+
【线性代数】第六章:特征值与特征向量
文章目录 一. 基本内容与重要结论1. 特征值、特征向量、特征方程的概念2. 矩阵相似 二. 重要定理1. 特征向量的有限次变换,还是特征向量2. 特征值与特征矩阵的关系3. 特征值与特征向量的相关性4. 相似则有相同的特征值(只是必要条件)4.1. 相似的四个必要条件5. 矩阵对角化相关定理5.1. 可对角化的充要条件5.2. 实对称矩阵必可对角化 6. **Schmidt**正交化方法
【数学】如何求解矩阵的特征值和特征向量
文章目录 如何求解矩阵的特征向量背景公式示例题目详细讲解Python代码求解实际生活中的例子本质解释 如何求解矩阵的特征向量 背景 特征向量和特征值是线性代数中的重要概念,广泛应用于物理学、计算机科学(如机器学习、图像处理)和统计学等领域。特征向量描述了线性变换中不改变方向的向量,而特征值描述了这些向量被拉伸或压缩的程度。 公式 求解矩阵的特征向量需要用到特征值方程:
利用QR算法求解矩阵的特征值和特征向量
利用QR算法求解矩阵的特征值和特征向量 为了求解一般矩阵(不是那种幼稚到shi的2 x 2矩阵)的特征值. 根据定义的话,很可能需要求解高阶方程... 这明显是个坑...高阶方程你肿么破... 折腾了好久 1.我要求特征值和特征向量. 2.找到一种算法QR分解矩阵求解特征值 3.QR矩阵分解需要Gram-schimidt正交化分解 有一种很明显的感觉,往往在现在很难有 很系统 很深
线性代数|机器学习-P5特征值和特征向量
文章目录 1. 特征值和特征向量1.1 特征向量1.2 向量分解 2. 矩阵相似2.1 特征值求解法-相似2.2 特殊特征值2.3 反对称矩阵 3.对称矩阵 1. 特征值和特征向量 1.1 特征向量 假设有一个n行n列的方阵A,有 n 个不相同的特征值为 λ \lambda λ,特征向量为 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x
总结r(A)=1的矩阵特征向量与特征值
r(A)=1的矩阵,天生有当特征值为0时的n-1个线性无关的特征向量。 方程组:Ax = 0,根据系数矩阵的秩为1,因此解向量有n-1个线性无关向量。 也即矩阵A至少有n-1重特征值 λ=0 \lambda = 0 再由 ∑ni=1λi=∑ni=1aii \sum_{i=1}^n\lambda_i = \sum_{i=1}^na_{ii} 可以求得 λn \lambda_n,这个需要具体问
PCA算法:从一组照片中获取特征脸(特征向量)
本文介绍了对一组照片进行PCA处理的过程和结果。本文使用OpenCV的PCA处理函数,参考了夏天的味道的博客opencv pca。本文使用的照片来源于YelaFaces(直接Baidu就能找到在CSDN上的下载链接,就不上传了)。 一、操作步骤 PCA处理的基本步骤为: 1、获取m个样本,每个样本有n个特征。 2、每个样本作为一行,构成m*n的举证A。 3、将矩阵转置再乘以自己得到C=A
【python】numpy库计算矩阵特征值和特征向量
目录 0.环境 1.前提 2.全部代码 0.环境 windows + eclipse + python 1.前提 我的邻接矩阵是固定的,11*11 2.全部代码 要将邻接矩阵使用numpy赋值 #计算矩阵特征值import numpy as npA = np.array([[0,1,1,1,1,1,1,1,1,1,1], [1,0,0,0,0,0,0,0,0,
图像算法的基础知识(双线性插值,协方差矩阵,矩阵的特征值、特征向量)
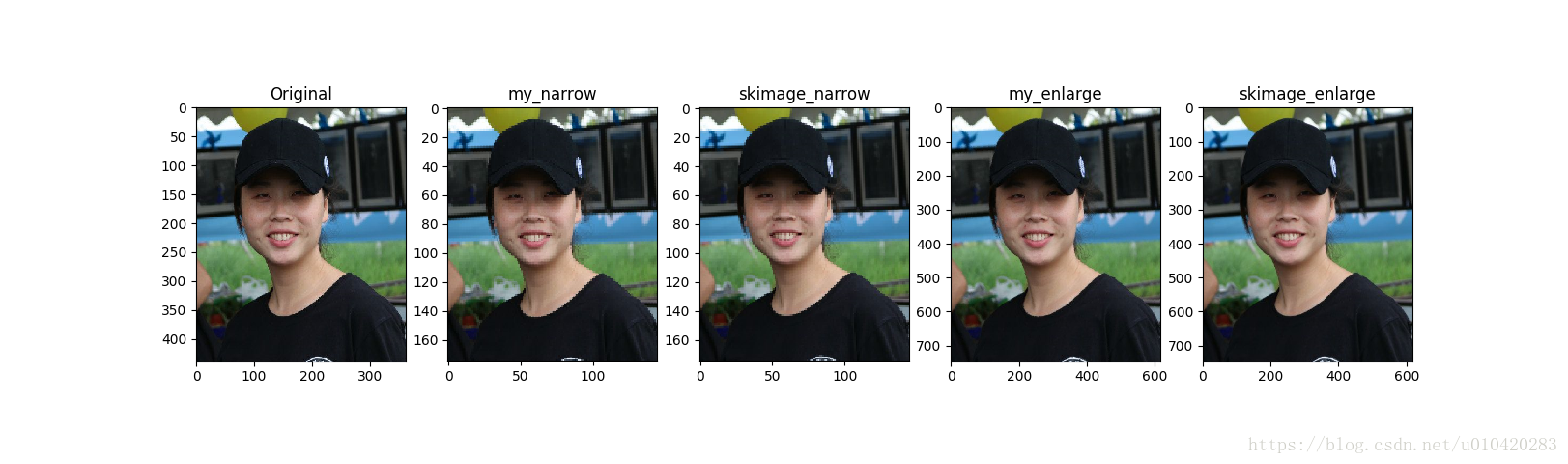
0. 前言 MATLAB或者OpenCV里有很多封装好的函数,我们可以使用一行代码直接调用并得到处理结果。然而当问到具体是怎么实现的时候,却总是一脸懵逼,答不上来。前两天参加一个算法工程师的笔试题,其中就考到了这几点,感到非常汗颜!赶紧补习! 1. 双线性插值 在图像处理中,我们有时需要改变图像的尺寸,放大或者缩小。线性插值则是这类操作的关键算法。不管是放大还是缩小操作,其实都是一个像素映射
【白话机器学习系列】白话特征向量
白话特征向量 一个方阵 A A A 与列向量 v v v 的乘积会生成一个新的列向量。这个新向量通常与原向量有着不同的方向,矩阵在这里代表一个线性变换。然而,某些向量会保持其原始方向。我们称这种向量为矩阵 A A A 的特征向量(eigenvector)。 在本文中,我们将探讨特征向量、特征值和矩阵的特征方程。并且以 2 维方阵为例,教大家如何计算矩阵的特征向量和特征值。
特征值与特征向量 转自别人的
§4.1 特征值与特征向量 §4.1.1特征值与特征向量的概念及其计算 定义1. 设A是数域P上的一个n阶矩阵,l是一个未知量, 称为A的特征多项式,记 ¦(l)=| lE-A|,是一个P上的关于 l 的n次多项式,E是单位矩阵。 ¦(l)=| lE-A|=ln+a1ln-1+…+an= 0是一个n次代数方程,称为A的特征方程。 特征方程 ¦(l)=| lE
特征值eigenvalue与特征向量eigenvector
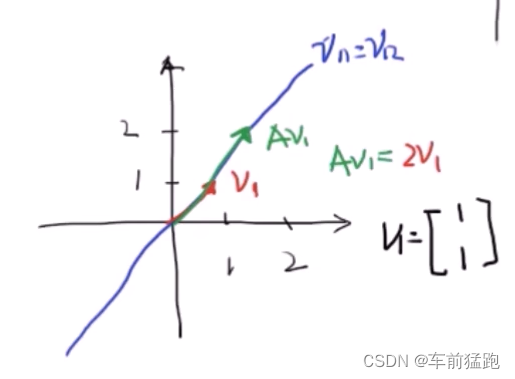
特征值,特征向量概念 在线性代数中,对于一个给定的线性变换A,他的特征向量v经过这个线性变换的作用之后,得到的新向量仍然与原来的 v v v保持在同一条直线上。但长度或方向也许会改变。即: A v Av Av = λ v \lambda v λv 其中 λ \lambda λ为标量,即特征向量的长度在该线性变换下缩放的比例,称为其特征值。 A = [ 1 1 4 − 2 ] , v 1
NLTK(9.2)生成特征向量与文本相似度
文章目录 生成对应特征向量 生成对应特征向量 几种文本特征向量化方法 1.词集模型:one-hot编码向量化文本(统计各词在文本中是否出现) 2.词袋模型:文档中出现的词对应的one-hot向量相加(统计各词在文本中出现次数,在词集模型的基础上。) 3.词袋模型+IDF:TFIDF向量化文本(词袋模型+IDF值,考虑了词的重要性) 4.N-gram模型:考虑了词的顺序
MATLAB 构建协方差矩阵,解算特征值和特征向量(63)
MATLAB 局部点云构建协方差矩阵,解算特征值和特征向量(63) 一、算法介绍二、算法实现1.代码2.结果 一、算法介绍 对于某片有待分析的点云,我们希望构建协方差矩阵,计算特征值和特征向量,这是很多算法必要的分析方法,这里提供完整的计算代码(验证正确) !!! 特别需要注意的是:特征值的排序方式 这里计算的特征值按照从小到大的顺序重新排列得到:L1 > L2 >
【矩阵论】11——Jordan标准型——线性变换的特征值与特征向量
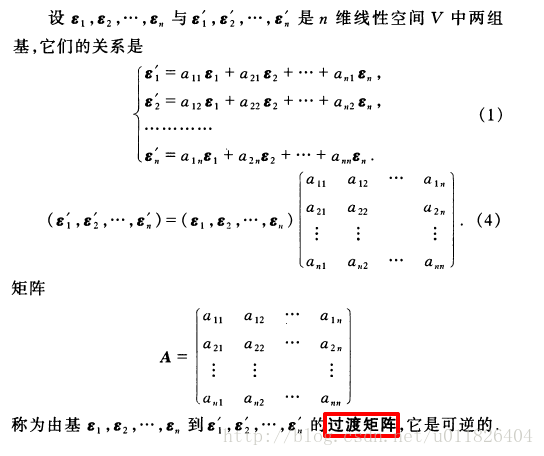
本系列文章由Titus_1996 原创,转载请注明出处。 文章链接:https://blog.csdn.net/Titus_1996/article/details/83177254 本系列文章使用的教材为《矩阵论》(第二版),杨明,刘先忠编,华中科技大学出版社。 定义 假设T在某组基{α1,α2,...αn}下的矩阵为A,ξ是T关于λ的特征向量。则有 ξ=(α1,α2,..
特征值和特征向量在现代控制理论的简单应用
参考视频:https://www.bilibili.com/video/BV1fx41137Zm 在线性代数中,对于一个给定的线性变换A,它的特征向量经过这个线性变换的作用之后,得到的新向量仍然与原来的v保持在同一条直线上,但长度或方向也许会改变,即: A v = λ v Av = \lambda v Av=λv 其中 λ \lambda λ为标量,即特征向量的长度在该线性变换下缩放的比例,称其