本文主要是介绍特征值eigenvalue与特征向量eigenvector,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
特征值,特征向量概念
在线性代数中,对于一个给定的线性变换A,他的特征向量v经过这个线性变换的作用之后,得到的新向量仍然与原来的 v v v保持在同一条直线上。但长度或方向也许会改变。即:
A v Av Av = λ v \lambda v λv
其中 λ \lambda λ为标量,即特征向量的长度在该线性变换下缩放的比例,称为其特征值。
A = [ 1 1 4 − 2 ] , v 1 = [ 1 2 ] A = \left[ \begin{array}{cc} 1 & 1 \\ 4 & -2 \end{array} \right],v_{1}=\left[ \begin{array}{cc} 1\\ 2 \end{array} \right] A=[141−2],v1=[12]
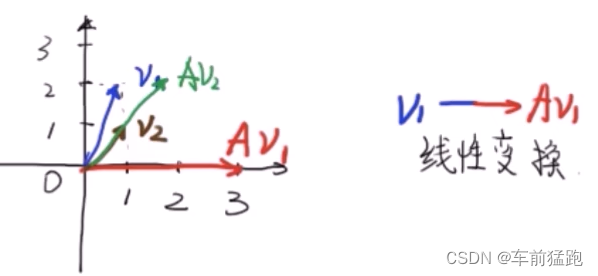
A与 v 1 v_{1} v1内积后的A v 1 v_{1} v1与 v 1 v_{1} v1不在一条直线上,所以 v 1 v_{1} v1不是A的特征向量
A v 1 = [ 3 0 ] Av_{1}=\left[ \begin{array}{cc} 3\\ 0 \end{array} \right] Av1=[30]
v 2 v_{2} v2 = [ 1 1 ] \left[ \begin{array}{cc} 1\\ 1 \end{array} \right] [11]
A v 2 Av_{2} Av2 = [ 1 1 4 − 2 ] \left[ \begin{array}{cc} 1 & 1 \\ 4 & -2 \end{array} \right] [141−2] [ 2 2 ] \left[ \begin{array}{cc} 2\\ 2 \end{array} \right] [22] = [ 2 2 ] \left[ \begin{array}{cc} 2\\ 2 \end{array} \right] [22] = 2 [ 1 1 ] \left[ \begin{array}{cc} 1\\ 1 \end{array} \right] [11] = 2 v 2 v_{2} v2
v 2 v_{2} v2经过A线性变换后的A v 2 v_{2} v2与 v 2 v_{2} v2在同一条直线上。
那么 v 2 v_{2} v2是A的特征向量,2是A的特征值。
求解特征值,特征向量?
A v = λ v ⟹ A v − λ v = 0 Av = \lambda v \Longrightarrow Av - \lambda v = 0 Av=λv⟹Av−λv=0
( A − λ I ) v = 0 (A - \lambda I)v = 0 (A−λI)v=0, I I I是单位矩阵
上面的式子有非零解, ∣ A − λ I ∣ |A-\lambda I| ∣A−λI∣行列式必须为0
举个例子
- 这是一个矩阵(线性变换)
A = [ 1 1 4 − 2 ] A = \left[ \begin{array}{cc} 1 & 1 \\ 4 & -2 \end{array} \right] A=[141−2] - 让A与 λ I \lambda I λI相减
A − λ I = [ 1 − λ 1 4 − 2 − λ ] A - \lambda I = \left[ \begin{array}{} 1 - \lambda & 1 \\ 4 & -2 - \lambda \end{array} \right] A−λI=[1−λ41−2−λ] - 行列式相减等于0
∣ A − λ I ∣ = 0 ⟹ ∣ 1 − λ 1 4 − 2 − λ ∣ = 0 |A - \lambda I| = 0 \Longrightarrow \begin{vmatrix}{} 1 - \lambda & 1 \\ 4 & -2 - \lambda \end{vmatrix} = 0 ∣A−λI∣=0⟹ 1−λ41−2−λ =0 - 行列式计算,解一元二次方程方程
( 1 − λ ) ( − 2 − λ ) − 1 × 4 = 0 ⟹ { λ 1 = 2 λ 2 = − 3 } (1 - \lambda)(-2 - \lambda) - 1 \times 4 = 0 \Longrightarrow \begin{Bmatrix} \lambda_1=2 \\\lambda_2=-3 \end{Bmatrix} (1−λ)(−2−λ)−1×4=0⟹{λ1=2λ2=−3}
得到了2个特征值: 2 , − 3 2,-3 2,−3 - 当 λ 1 = 2 \lambda_{1}=2 λ1=2时,有 A = [ 1 − 2 1 4 − 2 − 2 ] ⋅ v 1 = 0 A = \left[ \begin{array}{cc} 1-2 & 1 \\ 4 & -2 - 2 \end{array} \right] \cdot v_{1} = 0 A=[1−241−2−2]⋅v1=0,这是对应与 λ 1 \lambda_{1} λ1的特征向量
[ 1 − 2 1 4 − 2 − 2 ] ⋅ [ v 11 v 12 ] ⟹ { − v 11 + v 12 = 0 4 v 11 − 4 v 12 = 0 } ⟹ v 11 = v 12 \left[ \begin{array}{cc} 1-2 & 1 \\ 4 & -2 - 2 \end{array} \right] \cdot \left[ \begin{array}{} v_{11}\\v_{12} \end{array} \right] \Longrightarrow \begin{Bmatrix} -v_{11} + v_{12} = 0\\ 4v_{11} - 4v_{12} = 0 \end{Bmatrix} \Longrightarrow v_{11}=v_{12} [1−241−2−2]⋅[v11v12]⟹{−v11+v12=04v11−4v12=0}⟹v11=v12
- 解方程的结果是 v 11 = v 12 v_{11} = v_{12} v11=v12,那么在蓝色线上的任一个向量都是A的特征向量
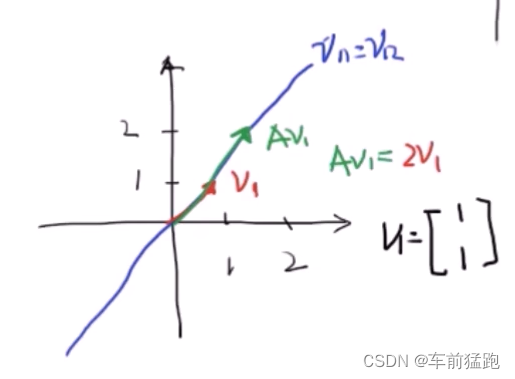
取任意一组解: { v 11 = 1 v 12 = 1 } \begin{Bmatrix} v_{11} = 1\\v_{12} = 1\end{Bmatrix} {v11=1v12=1}就可得到矩阵的特征向量。
同理可以计算出特征值 λ 2 = − 3 \lambda_{2} = -3 λ2=−3时, { v 21 = 1 v 22 = − 4 } \begin{Bmatrix}v_{21}=1\\v_{22}=-4\end{Bmatrix} {v21=1v22=−4},此时特征向量 v 2 = [ 1 − 4 ] v_2=\left[\begin{array}{}1\\-4\end{array}\right] v2=[1−4]
这篇关于特征值eigenvalue与特征向量eigenvector的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!