字符串的特征向量与KMP算法

本文主要是介绍字符串的特征向量与KMP算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

字符串的特征向量就是由字符串各位置上的特征数构成的一个向量。设字符串为P，令Pi为从字符串首字母到第i个位置的前缀，则字符串P的i位置上的特征数就是Pi的首尾非空真子串匹配的最大长度。例如：字符串abcdaabcab的特征向量是(0,0,0,0,1,1,2,3,1,2)。其中第5个位置的特征数是1，因为P5是abcdaa，首尾非空真子串能够匹配的就是a；而第7个位置的特征数是3，因为P7是abcdaabc，首尾非空真子串能够匹配的是abc。0位置上的特征数显然为0。暴力法求特征向量显然是非常耗时的，实际上可以基于这样一个思路求特征向量：从0位置开始求特征数，i位置上的特征数是由之前位置的特征数决定的。

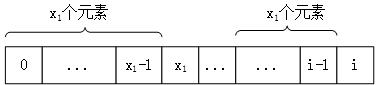
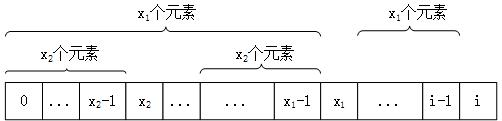
用Next数组表示字符串的特征向量。如上所示，假设Next[i-1]==x1，也就是说i-1位置上首尾x1个元素是匹配的。很显然，当P[i]==P[x1]时，i位置上首尾至少有x1+1个元素匹配，实际上就是x1+1个。

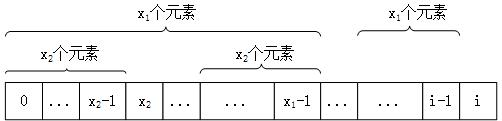
当P[i]!=P[x1]时，考查Next[x1-1]，假设其值为x2，这说明在x1-1位置上首尾x2个元素相等，此时，如果P[i]==P[x2]，则说明i位置首尾至少有x2+1个元素是匹配的，实际上就是x2+1个。如果P[i]!=P[x2]，则可以考查Next[x2-1]，依次类推。直到x的值为0，此时如果P[i]==P[x]，则特征数为x+1也就是1，否则就是0。上述过程并不是算法的充分条件，只是由特征向量推出的性质；当然理论上也早有证明，这个性质是可以用来求出特征向量的。
POJ2406是一道利用特征向量的简单题目。假设字符串s是另外一个字符串的t的n次方，即s是由t重复n次得到的，那么最后一个位置上的首尾匹配的真子串一定是s-t，而t的长度一定是s的长度减去s最后一个位置上的特征数，且s的长度一定是t长度的整数倍。这也是由n次方得到的性质，但是利用这个性质一样可以证明s一定是t的n次方。

//令字符串S=s^n，求最大的n
//例如aaaa = a^4 = (aa)^2，则答案是4
//如果S长度为L,s的长度为l,则S最后一个特征数一定是L-l
//而且L是l的n倍
#include <cstdio>
#include <cstring>
using namespace std;
#define SIZE 1000005void getNext(char const P[],int n,int next[]){next[0] = 0;for(int i=1;i<n;++i){int k = next[i-1];while( k > 0 && P[k] != P[i] ) k = next[k-1];next[i] = ( P[i] == P[k] ) ? k + 1 : 0;}return;
}char P[SIZE];
int Next[SIZE];
int main() {while( scanf("%s",P) ){if ( '.' == *P && '\0' == P[1] ) return 0;int len = strlen(P);getNext(P,len,Next);if ( len % ( len - Next[len-1] ) ) printf("1\n");else printf("%d\n",len/(len-Next[len-1]));}return 0;
}

令目标为T，模式为P，问P是否为T的子串，这就是字符串匹配问题。暴力法很容易想到，每当不匹配的时候，将P后移一个位置，再次尝试匹配。KMP算法的关键就在于当不匹配时，P是否只能往后移动一位？

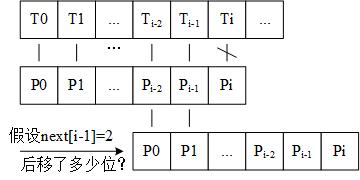
上图很明显显示了：当Pi与对应的Ti字母不相等时，P可以往后移多位。假设next[i-1]==2，则P应该往后移动i-2位再进行匹配。一般的，应该往后移动i-next[i-1]位。例如：abcdaabcab的特征向量是(0000112312)，假设T1是abcz….，则当比较到第3位的时候字母不匹配，此时应该把P后移3-next[2]也就是3位，再进行比较；假设T2是abcdaabcz…，则当比较到第8位的时候不匹配，此时应该将P后移到8-next[7]也就是5位，再开始比较。
不过，特别要注意的是：在上图中，P后移了i-next[i-1]位以后（假设next[i-1]是2），P0还需要与T[i-2]进行比较吗？P1还需要与T[i-1]进行比较吗？不需要，因为可以确定是相等的，只需从Ti和P2开始往下比较。所以很重要的一点：KMP算法中，T的字母只访问一次，T中已经比较过的字母不需要再次与P去比较，T的下标不存在回溯。所以KMP算法是线性时间的。对P而言，当Pi字母与T对应字母不匹配时，需要从P的第next[i-1]个字母重新开始比较。在上图中，就是要从第2个字母开始比较。在T2的例子中，T2是abcdaabcz…，P是abcdaabcad，当第8个字母a与T的字母z不匹配的时候，我们只需从P中的第3个字母d开始再跟T比较。
所以，我们可以重新定义特征数和特征向量，i位置的特征数就是当i位置的字母不匹配的时候，P的下标需要重新定位的位置。特别的当第0个位置不匹配时，令next[0]==-1，表示P的下标仍然维持在0，但T的下标要往后移一位。于是P: abcdaabcad的KMP匹配算法的特征向量是(-1,0,0,0,0,1,1,2,3,1)。
KMP算法仍然有优化的可能，当T3是abcdaaz…时，比较到第6个字母，P的下标应该回溯到几？按上述值应该是1，但其实可以回到0。假设T4是abcdz…，当比较到第4个字母不匹配时，P的下标应该回到几？可以回到0，但实际上T的这个字母不用再比较了，所以在P的下标回到0的同时，T的下标应该加1。这种操作恰好是特征向量为-1时应该进行的操作。

如上，令i的特征数是x1，即当Pi不匹配时，P下标应该回到x1。但是当P[i]==P[x1]时，下标还可以再往前。令x1位置的特征数是x2，则显然下标可以回到x2，当P[i]!=P[x2]时。否则，下标还可以往前，如此反复直到0位置。如果P[i]==P[0]，则i位置的特征数应该是-1，表示此位置不匹配时，P的下标维持在0，而T的下标加1。字符串abcdaabcab优化过后的特征向量应该是(-1,0,0,0,-1,1,0,0,3,0)。
hdu1711是标准的KMP问题，只不过匹配的不是字符串，而是整数序列。

//KMP算法，匹配的不是字符序列，而是整数
#include <cstdio>
using namespace std;
int T[1000005];
int P[10005];
int Next[10005];
void getKMPNext(int const P[],int n,int next[]){next[0] = -1;int i = 0, k = -1;while( i < n ){while( k >= 0 && P[i] != P[k] )k = next[k];++i,++k;if ( i == n ) return;next[i] = ( P[i] == P[k] ) ? next[k] : k;}
}
//在T中搜索P，输出第一个找到的位置，否则输出-1
int KMP(int const T[],int tn,int const P[],int pn,int const next[]){if ( pn > tn ) return -1;int tp = 0, pp = 0;while( tp < tn ){if ( -1 == pp || T[tp] == P[pp] ) ++tp,++pp;else pp = next[pp];if ( pn == pp ) return tp - pp;}return -1;
}
int main() {int nofkase;scanf("%d",&nofkase);while(nofkase--){int tn,pn;scanf("%d%d",&tn,&pn);for(int i=0;i<tn;++i)scanf("%d",T+i);for(int i=0;i<pn;++i)scanf("%d",P+i);getKMPNext(P,pn,Next);//从1开始索引int t = KMP(T,tn,P,pn,Next);printf("%d\n",(-1==t)?-1:t+1);}return 0;
}