本文主要是介绍矩阵理论基础知识(1)--特征值与特征向量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
之所以想起来总结这部分的知识,也是由于目前学习的机器学习算法中,矩阵论/矩阵分析呈刷屏似的出现,而之前本科阶段的高等代数中,总是只知道有这么个东西,也初略知道怎么计算,但不知道其中的真正含义,因此这两天决定将这块知识汇总下,知其然也知其所以然。
首先介绍几个基本的概念:
- 向量组线性无关:向量组中的任何一个向量都不能被其它向量线性表出。即当且仅当k1=k2…=kr=0时,k1α1+k2α2+…+krαr=0成立。
- 维度:如果线性空间V中最多只能有n个线性无关的向量,则称线性空间V是n维的。
- 基:在n维线性空间V中,n个线性无关向量称为V的一组基,V中任何的向量都可以由这组基来表出,即:a=a1e1+a2e2+…+anen,这时这组基前面的系数就成为该向量的坐标(a1,a2,…an)。讲到这里,就与我们之前接触的东西很相似了,事实上我们最常用的二维空间即建立在(1,0),(0,1)这组基上,三维空间建立在(1,0,0),(0,1,0),(0,0,1)这组基上。
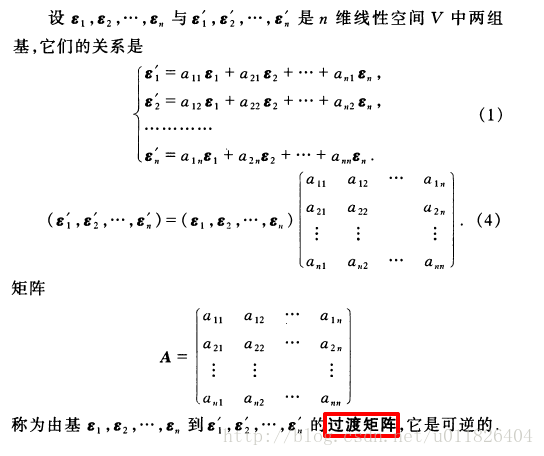
(1)基变换与坐标变换
这篇关于矩阵理论基础知识(1)--特征值与特征向量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






