利用QR算法求解矩阵的特征值和特征向量

本文主要是介绍利用QR算法求解矩阵的特征值和特征向量，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

利用QR算法求解矩阵的特征值和特征向量

为了求解一般矩阵(不是那种幼稚到shi的2 x 2矩阵)的特征值．
根据定义的话，很可能需要求解高阶方程．．．
这明显是个坑．．．高阶方程你肿么破．．．

折腾了好久
1.我要求特征值和特征向量．
2.找到一种算法QR分解矩阵求解特征值
3.QR矩阵分解需要Gram-schimidt正交化分解

有一种很明显的感觉，往往在现在很难有　很系统　很深入　的学习某一个学科的某一门知识．
往往学的时候＂靠，学这东西有什么用＂＂学了这么久，也不知道怎么用，不想学＂
到后来要解决问题的时候，要解决问题很可能这个问题里包含其他子问题，自问题里又有自问题，一层层的递归下去，直到解决所有子问题，才能递归回去，解决我们最初想搞定的问题．

又会懊恼，没有很系统的学习过那门知识．

骚年，Hold 住，你能递归的去死磕一个问题多深，如果你能安全的返回到原来你最初想要解决的问题，没有＂爆栈＂，那么这个深度就代表你的学习能力．深度越深，学习能力是越强的．人不可能一直拥有一个足够舒适的环境去系统的把所有东东都搞定，不可能把所有的基础知识都搞定了再上项目，去解决实际问题．在实际问题中发现问题，解决问题，才是真真的学习能力！！！不是TM卷子上多少分！给朕Hold住！

---

啊，呼喊万能的wiki帝
http://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors

先回顾一下对于一般的矩阵求特征值是怎么破的

你会发现，上帝啊，这家伙要求解方程．．．一般的二阶方程可能还能搞得定，但是矩阵的规模一大，高阶方程就坑爹了，你去求解高阶方程组？两个字，呵呵．当前我找到的可行解是矩阵的QR算法．

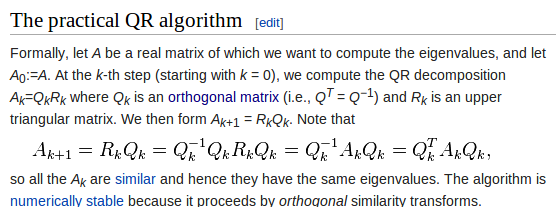
其实也没有什么难的，就是一次次的迭代，对矩阵A做QR分解，然后由于Ｑ是个正交阵他的逆和转置是一样的，所以你会看到上面图中的公式推到．
迭代次数足够多的时候，可以得到足够接近矩阵特征值的数值解．

再次强调，计算机只能求解数值解，不能求解析解．

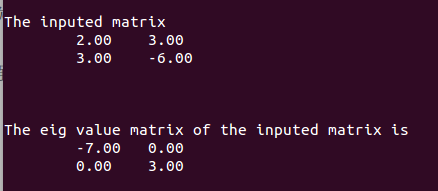
    def eig(self, A) :if A is None :returnfor i in range(0, 20) :(Q, R) = self.qr_decomposition(A)A = self.multiply(R, Q)return A

对角线上的就是矩阵的特征值

找到特征值之后根据

$$Ax = \beta x$$

然后对$A - \beta$矩阵求逆即可

输出的第一个矩阵的对角线上的都是特征值
函数实现:

    def eig(self, A) :if A is None :returntmp_mat = copy.deepcopy(A)for i in range(0, 20) :(Q, R) = self.qr_decomposition(tmp_mat)tmp_mat = self.multiply(R, Q)row = len(tmp_mat)col = len(tmp_mat[0])for i in range(0, row) :for j in range(0, col) :if i != j :tmp_mat[i][j] = 0eig_vec = self.inverse(self.sub(A, tmp_mat))return (tmp_mat, eig_vec)

以上函数实现中涉及的＂未知＂函数实现都能在线面的Link里面找到
http://blog.csdn.net/cinmyheart/article/details/43976423

如果你细心的话就会发现，上面的实现是无法对特征值为0的情况进行求解的，不然BUG．
注意事项 :
这里算法要求待求解矩阵是要满足行列式的值非0．即，矩阵的特征值不能为0．

推土机压过
旧日的家只剩下门前电线杆和灰蒙的天房檐下
伸手去捧雨天的房檐水屋后桔园里
从秋千上摔下边疼边笑日落时
有爷爷的三轮车从镇上回来门前
有人坐着小木凳
眨巴着眼
痴痴地等太阳不等你
我等你时间开着推土机
无情的碾过童年

摄于二零一五年二月六日

这篇关于利用QR算法求解矩阵的特征值和特征向量的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---