【线性代数】第六章：特征值与特征向量

本文主要是介绍【线性代数】第六章：特征值与特征向量，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本章要求

1. 要理解特征值、特征向量的概念，掌握矩阵特征值的性质，掌握求矩阵特征值、特征向量的方法.
2. 要理解矩阵相似的概念，掌握相似矩阵的性质，搞清矩阵能相似对角化的条件，掌握将矩阵化为相似对角矩阵的方法.
3. 要熟悉实对称矩阵特征值、特征向量的特殊性质，掌握用正交矩阵化实对称矩阵为对角矩阵的方法.

一. 基本内容与重要结论

1. 特征值、特征向量、特征方程的概念

 

跟齐次线性方程组结合 => 先求特征值然后再求特征向量

 

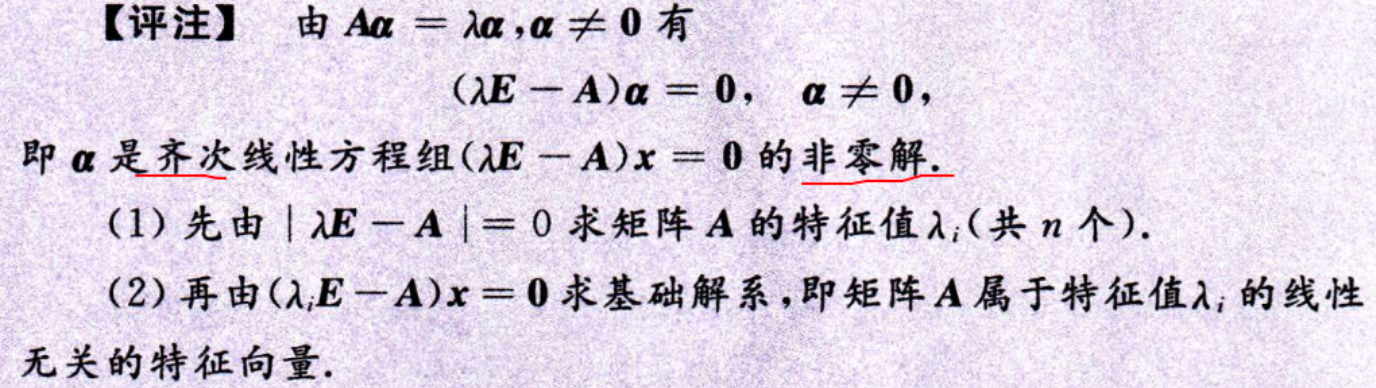
2. 矩阵相似

 

相似特性：

 

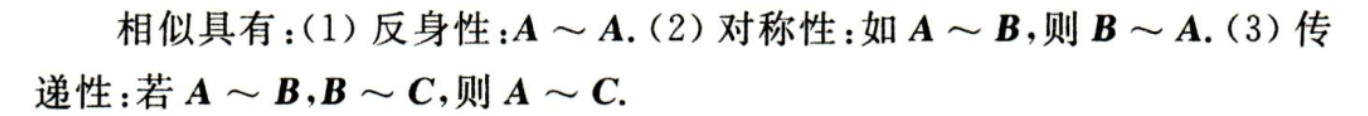
二. 重要定理

注意：每个特征值都会对应一个特征方程，通过特征方程来解对应特征值的特征向量。

1. 特征向量的有限次变换，还是特征向量

 

2. 特征值与特征矩阵的关系

 

3. 特征值与特征向量的相关性

 

 

4. 相似则有相同的特征值（只是必要条件）

 

4.1. 相似的四个必要条件

若矩阵A与矩阵B均为n阶方阵，则A与B相似的必要条件为：
1、A与B的特征值相同。
2、λE-A与λE-B等价。
3、tr(A)=tr(B)。 对角元素之和
4、|A|=|B|。

参考： 矩阵相似的四个必要条件及性质证明

 

5. 矩阵对角化相关定理

5.1. 可对角化的充要条件

 

 

每个特征值，该特征值的重数=其线性无关向量个数（因为每个特征值都会对应一个矩阵）。

 

5.2. 实对称矩阵必可对角化

 

如果两个实对称的矩阵的特征值相同，则说明两个矩阵相似。

根据实对称矩阵必能对角化+矩阵的对称性，传递性，能够说明，以上结论。

 
 

6. Schmidt正交化方法

 

这篇关于【线性代数】第六章：特征值与特征向量的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---