线性代数专题
线性代数|机器学习-P36在图中找聚类
文章目录 1. 常见图结构2. 谱聚类 感觉后面几节课的内容跨越太大，需要补充太多的知识点，教授讲得内容跨越较大，一般一节课的内容是书本上的一章节内容，所以看视频比较吃力，需要先预习课本内容后才能够很好的理解教授讲解的知识点。 1. 常见图结构 假设我们有如下图结构： Adjacency Matrix:行和列表示的是节点的位置，A[i,j]表示的第 i 个节点和第 j 个
线性代数|机器学习-P35距离矩阵和普鲁克问题
文章目录 1. 距离矩阵2. 正交普鲁克问题3. 实例说明 1. 距离矩阵 假设有三个点 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,三个点距离如下： ∣ ∣ x 1 − x 2 ∣ ∣ 2 = 1 , ∣ ∣ x 2 − x 3 ∣ ∣ 2 = 1 , ∣ ∣ x 1 − x 3 ∣ ∣ 2 = 6 \begin{equation} ||x
【线性代数】正定矩阵，二次型函数
本文主要介绍正定矩阵，二次型函数，及其相关的解析证明过程和各个过程的可视化几何解释（深蓝色字体）。 非常喜欢清华大学张颢老师说过的一段话：如果你不能用可视化的方式看到事情的结果，那么你就很难对这个事情有认知，认知就是直觉，解析的东西可以让你理解，但未必能让你形成直觉，因为他太反直觉了。 正定矩阵 定义 给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 ，有 恒成
python科学计算：NumPy 线性代数与矩阵操作
1 NumPy 中的矩阵与数组 在 NumPy 中，矩阵实际上是一种特殊的二维数组，因此几乎所有数组的操作都可以应用到矩阵上。不过，矩阵运算与一般的数组运算存在一定的区别，尤其是在点积、乘法等操作中。 1.1 创建矩阵 矩阵可以通过 NumPy 的 array() 函数创建。矩阵的形状可以通过 shape 属性来访问。 import numpy as np# 创建一个 2x3 矩阵mat
线性代数 第六讲 特征值和特征向量_相似对角化_实对称矩阵_重点题型总结详细解析
文章目录 1.特征值和特征向量1.1 特征值和特征向量的定义1.2 特征值和特征向量的求法1.3 特征值特征向量的主要结论 2.相似2.1 相似的定义2.2 相似的性质2.3 相似的结论 3.相似对角化4.实对称矩阵4.1 实对称矩阵的基本性质4.2 施密特正交化 5.重难点题型总结5.1 判断矩阵能否相似对角化5.2 已知两个矩阵相似，求某个矩阵中的未知参数5.3 相似时，求可逆矩阵P，使
【鼠鼠学AI代码合集#5】线性代数
在前面的例子中，我们已经讨论了标量的概念，并展示了如何使用代码对标量进行基本的算术运算。接下来，我将进一步说明该过程，并解释每一步的实现。 标量（Scalar）的基本操作 标量是只有一个元素的数值。它可以是整数、浮点数等。通过下面的 Python 代码，我们可以很容易地进行标量的加法、乘法、除法和指数运算。 代码实现： import torch# 定义两个标量x = torch.tens
线性代数|机器学习-P33卷积神经网络ImageNet和卷积规则
文章目录 1. ImageNet2. 卷积计算2.1 两个多项式卷积2.2 函数卷积2.3 循环卷积 3. 周期循环矩阵和非周期循环矩阵4. 循环卷积特征值4.1 卷积计算的分解4.2 运算量4.3 二维卷积公式 5. Kronecker Product 1. ImageNet ImageNet 的论文paper链接如下：详细请直接阅读相关论文即可 通过网盘分享的文件：image
Matlab初等数学与线性代数
初等数学 算术运算 基本算术 加法 +添加数字，追加字符串sum数组元素总和cumsum累积和movsum移动总和 A = 1:5;B = cumsum(A)B = 1×51 3 6 10 15 减法 -减法diff差分和近似导数 乘法 .*乘法*矩阵乘法prod数组元素的乘积cumprod累积乘积pagemtimes按页矩阵乘法 （自 R202
线性代数行列式概念的引进
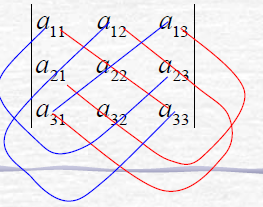
1 二阶行列式： 求这个方程组的解。 我们一般是用高斯消元法解这个方程组的。 为了记忆，我们引进记号（其实行列式刚开始，就是为了方便记忆）： 二阶行列式： 用高斯消元法求得的解可以表示为如下： 2 三阶行列式： 1) 六项的代数和。恰好是1,2,3这三个数的全排列的个数。 2) 每项都是3个元素的乘积，分析这3个元素的下标：他们取自不同行不
数学基础 -- 线性代数之矩阵的迹
矩阵的迹 什么是矩阵的迹？ 矩阵的迹（Trace of a Matrix）是线性代数中的一个基本概念，定义为一个方阵主对角线上元素的总和。矩阵的迹在许多数学和物理应用中都起着重要作用，例如在矩阵分析、量子力学、统计学和系统理论中。 矩阵迹的定义 对于一个 n × n n \times n n×n 的方阵 A A A： A = ( a 11 a 12 ⋯ a 1 n a 21 a 2
花书第二章——线性代数
2.1 标量、向量、矩阵、张量和转置 标量(scalar)：标量就是一个单独的数，例如数字1、2、1.1、1.2都是标量； 向量(vector)：一个向量可以看作是一组标量形成的一维数组，例如由 n 个实数组成的向量 x \pmb{x} x 为： x \pmb{x} x = [ x 1 , x 2 , … , x n x_1,x_2, \dots,x_n x1,x2,…,xn]。我
线性代数教材书籍推荐
INTRODUCTION TO LINEAR ALGEBRA, 线性代数导论，GILBERT STRANG ，有第六版中译本，网上也有第五版英文电子版，个人认为讲理论最好的教材 Practical Linear Algebra for Data Science，From Core Concepts to Applications Using Python, 个人认为讲理论结合应用最好的书籍，京东
线性代数 第五讲:线性方程组_齐次线性方程组_非齐次线性方程组_公共解同解方程组_详解
线性方程组 文章目录 线性方程组1.齐次线性方程组的求解1.1 核心要义1.2 基础解系与线性无关的解向量的个数1.3 计算使用举例 2. 非齐次线性方程的求解2.1 非齐次线性方程解的判定2.2 非齐次线性方程解的结构2.3 计算使用举例 3.公共解与同解3.1 两个方程组的公共解3.2 同解方程组 4.重难点题型总结4.1 抽象齐次线性方程组的求解4.1 含有系数的非齐次线性方程组的求
通义说【线性代数】什么是线性
线性关系是一种简单的数学关系，其中因变量（dependent variable）相对于自变量（independent variable）的变化率是常数，这意味着随着自变量的增加，因变量按照固定的比例增加或减少。这种关系可以用直线来表示。 线性函数具有以下性质： 叠加原理：两个线性函数的和仍然是线性的。齐次性：线性函数满足齐次性原则，即如果一个函数是线性的，那么这个函数的输出应当与输入成比例。无
线性代数|机器学习-P32循环矩阵的特征向量-傅里叶矩阵
文章目录 1. 大纲2. 循环矩阵2.1 移位矩阵P2.2 P的特征值和特征向量2.3 循环卷积矩阵2.4 循环卷积计算 3. 傅里叶矩阵 1. 大纲 循环矩阵在机器学习，图像处理中的应用循环卷积矩阵的特征值，特征向量，卷积规则循环卷积矩阵多项式表达： C = c 0 I + c 1 P + c 2 P 2 + ⋯ + c n − 1 P n − 1 C=c_0 I+c_1P+c
线性代数：线性代数（Linear Algebra）综述
文章目录 矩阵 / Matrix元素运算加法 A + B A+B A+B数量乘法 c A cA cA与向量之间的运算乘法 A b A\mathbf{b} Ab 与矩阵之间的运算矩阵乘法 乘方 性质方阵 / Square Matrix零矩阵对角矩阵 / Diagonal Matrix单位矩阵 / Identity Matrix转置 / Transpose逆矩阵 / Inverse Mat
NumPy（一）：简介【主要功能：操作数组、矩阵】【Python + NumPy == Matlab】【包括很多实用的数学函数】【覆盖了很多的数学领域， 比如：线性代数、傅里叶变换、随机数生成】
一、NumPy是什么？ NumPy是一个开源的Python科学计算库。 Numerical Python 二、NumPy有什么功能 NumPy主要的功能之一用来操作数组和矩阵。 NumPy是科学计算、深度学习等高端领域的必备工具。 使用TensorFlow、Caffe。框架训练神将网络模型时，需要进行大量复杂的计算，可以直接调用NumPy里面的API NumPy包含了很多实用的数学函数
数学基础 -- 线性代数之共轭转置矩阵
共轭转置矩阵 1. 共轭转置矩阵的定义 共轭转置矩阵（Hermitian transpose）是线性代数中的一个重要概念，特别是在处理复数矩阵时经常使用。它的定义包括两个步骤： 转置：将矩阵的行和列互换。共轭：对矩阵中的每个元素取复共轭，即将复数的虚部取负。 数学表达 对于一个 m × n m \times n m×n 的复矩阵 A A A ，其共轭转置矩阵 A † A^{\dag
通义说【线性代数】线性方程组和线性代数的关系
线性方程组和线性代数之间有非常紧密的关系。事实上，线性方程组是线性代数的一个核心主题，而线性代数提供了解决线性方程组的一系列理论和工具。 线性方程组 线性方程组是由一组线性方程构成的集合，每个方程都表示未知变量的线性组合等于一个常数项。一个典型的线性方程组可以写作： a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 +
通义说【线性代数】为什么矩阵乘以向量是一个对矩阵中列向量的线性组合
矩阵乘以向量可以被理解为该向量在矩阵所代表的空间变换下的映射结果，也可以看作是矩阵列向量的线性组合。为了更好地理解这一点，让我们从矩阵乘法的基本定义出发。 假设有一个 m × n m \times n m×n的矩阵 A A A和一个 n n n维列向量 x \mathbf{x} x，矩阵 A A A可以写成由它的列向量组成的集合，即： A = [ a 1 , a 2 , … , a n ]
AI学习记录 - 线性代数（3Blue1Brown）
一天更新一点点，只更新重点内容，一句话定义，简单的定义，避免脑子及记太多 向量的加法就是一种趋势运动 向量的延长缩短，就是分量的延长缩短 基向量就是在平面或者任意维度空间随便定义的一个向量 多个基向量的组合可以构成其它向量 两个基向量可以组合成平面的所有向量，三个基向量可以组合成空间的所有向量 矩阵乘法公式 一种理解方式：（-3，-1）和（1, 2）是两个新基向量，两个新
线性代数|机器学习-P31完成一个秩为1的矩阵
文章目录 1. 大纲2. 填充秩1矩阵2.1 举例2.2 二分图 3. 循环卷积矩阵 1. 大纲 给定一个秩为1的矩阵A，m行，n列，如果在矩阵A中给定m+n-1 个非零的值，请问如何填充这个矩阵A,使得矩阵A 填满？卷积和循环卷积矩阵，通过信号与系统中的卷积方式处理相关数据，求循环卷积矩阵的特征值和特征向量？ 2. 填充秩1矩阵 2.1 举例 假设我们有一个矩阵A，我们定
2.2线性代数的力量
欢迎来到线性代数的世界，这里是量化交易的健身房，我们的目标是让你的大脑肌肉变得强大，以便在金融市场上大展拳脚。别担心，即使你在大学时数学成绩可能只比体育课成绩好那么一点点，我也会用最通俗易懂的方式，让你领略到线性代数的魅力。 向量、矩阵与线性变换 首先，让我们从向量开始。想象一下，你手里拿着一个箭头，这个箭头有方向也有长度，这就是向量。在量化交易中，我们可以把股票价格的变化想象成向量，方向代表
数学基础 -- 线性代数之矩阵因式分解
矩阵因式分解 矩阵因式分解是线性代数中的重要工具，能够将复杂的矩阵运算简化。不同的分解方法适用于不同类型的矩阵，本文将详细介绍常见的矩阵因式分解方法及其适用的矩阵特点。 1. LU分解（LU Decomposition） 定义 LU分解将一个方阵 A A A 分解为两个矩阵的乘积：一个下三角矩阵 L L L 和一个上三角矩阵 U U U： A = L U A = LU A=LU
Games101学习 - 线性代数综述
1. 叉积矩阵形式 叉乘矩阵形式通常在物理模拟中有运用，处理四元数旋转也类似这样的形式。 // 定义两个向量 A 和 BFVector A(1.0f, 2.0f, 3.0f);FVector B(4.0f, 5.0f, 6.0f);// 计算叉积FVector CrossProduct = FVector::CrossProduct(A, B);if (GEngine){GEngine