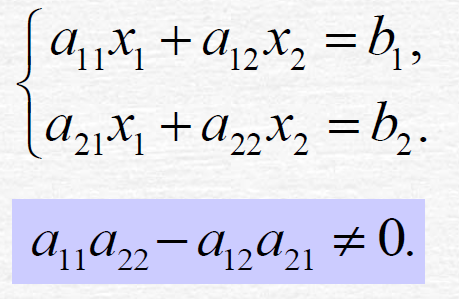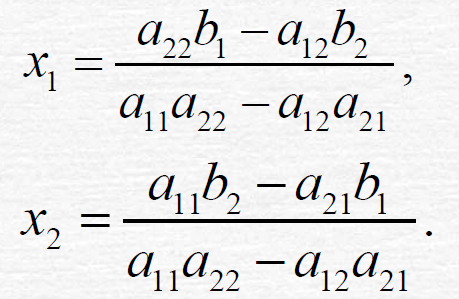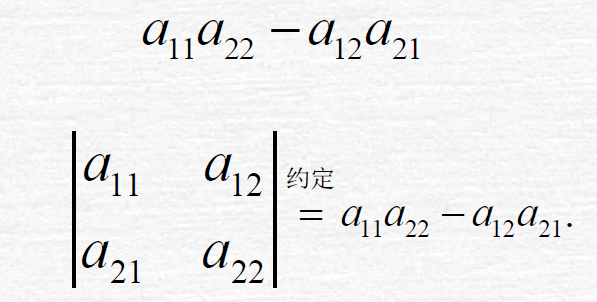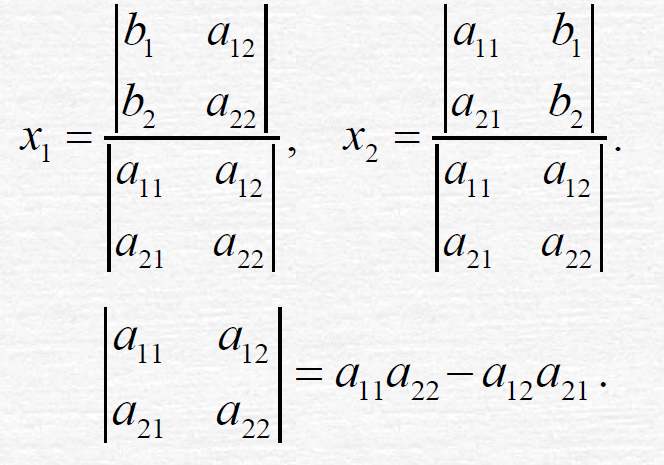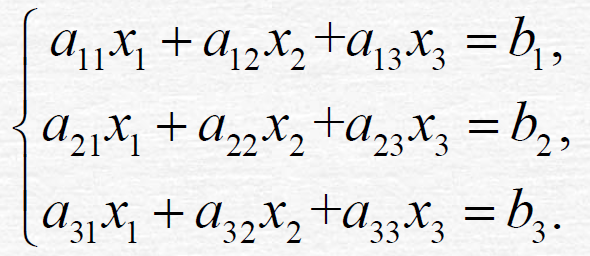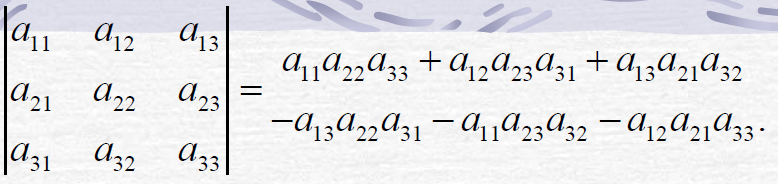本文主要是介绍线性代数行列式概念的引进,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 二阶行列式:
求这个方程组的解。
我们一般是用高斯消元法解这个方程组的。
为了记忆,我们引进记号(其实行列式刚开始,就是为了方便记忆):
二阶行列式:
用高斯消元法求得的解可以表示为如下:
2 三阶行列式:
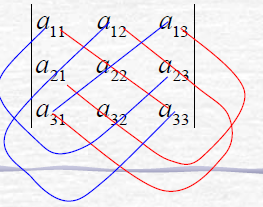
1) 六项的代数和。恰好是1,2,3这三个数的全排列的个数。
2) 每项都是3个元素的乘积,分析这3个元素的下标:他们取自不同行不同列。
这篇关于线性代数行列式概念的引进的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!