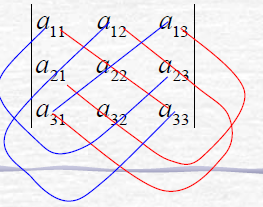
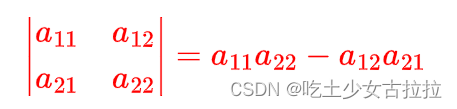行列式专题

【高等代数笔记】（18）N阶行列式

2. N阶行列式 2.12 行列式按k行（列）展开【拉普拉斯定理】 n n n阶矩阵 A = ( a i j ) \boldsymbol{A}=(a_{ij}) A=(aij)，取定第 i 1 , i 2 , . . . , i k i_{1},i_{2},...,i_{k} i1,i2,...,ik行（其中 i 1 < i 2 < . . . < i k i_{1}<i_{2}<.

线性代数行列式概念的引进

1 二阶行列式：求这个方程组的解。我们一般是用高斯消元法解这个方程组的。为了记忆，我们引进记号（其实行列式刚开始，就是为了方便记忆）：二阶行列式：用高斯消元法求得的解可以表示为如下： 2 三阶行列式： 1) 六项的代数和。恰好是1,2,3这三个数的全排列的个数。 2) 每项都是3个元素的乘积，分析这3个元素的下标：他们取自不同行不

《高等代数》行（列）和相等行列式

说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。注：1）行（列）和相等行列式的求解方法是将其于行都加到第一行（列），然后再提取第一行（列），使得第一行（列）变成“1”，再用第一行（列）将行列式化为三角形行列式。

《高等代数》范德蒙德行列式的应用

说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。注：范德蒙德行列式的简单应用及其变形。范德蒙德行列式的计算公式：注：（1）用大下标减去小下标。（2）i>j,不是i≥j 例一：（公式的简单应用）例二：（缺失的范德蒙德行列式一）注：1）可以看到，所要求的行列式与范德蒙德行列式相比缺失了次数为三次方的一行。利用行列

《高等代数》两条线行列式

说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。注：两条线行列式的固定做法为按照第一列展开。

《高等代数》“爪”字型行列式

说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。注：1）“爪”字型行列式的第一种求解方法是利用初等行（列）变换，将第一列除第一行的第一个数以外的其它数都化为0，得到三角行列式，然后进行求解。 2）“爪”字型行列式的第二种求解方法是“加边法”，其目的也是最终将行列式化为三角行列式进行求解。

行列式的计算（矩阵外面加个绝对值）

1、写在前面我表示很难过，曾经线代，矩阵学的也不算太差，可惜太久没用，导致现在连最基本的行列式都不会了。以后还是要多用，多用，多用，重要的事情说三遍。 2、行列式的计算准则定义：n阶行列式等于所有取自不同行不同列的n个元素的乘积的代数和，这里是1,2，...，n的一个排列，每一项都按下列规则带有符号：当是偶排列时带有正号，当是奇排列时带有负号。这一定义可写成这里表

【解析几何笔记】6.三阶行列式

6. 三阶行列式 6.1 三阶行列式的定义对三阶方阵 ( a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ) \begin{pmatrix} a_{1} & a_{2} & a_{3}\\ b_{1} & b_{2} & b_{3}\\ c_{1} & c_{2} &c_{3} \end{pmatrix} a1b1c1a2b2c2a3b3c

行列式和矩阵的区别

目录一、行列式 1. 行列式的定义 2. (全)排列 3. 逆序数二、矩阵 1. 矩阵的定义三、行列式和矩阵的区别四、参考书目一、行列式 1. 行列式的定义 2. (全)排列 3. 逆序数二、矩阵 1. 矩阵的定义三、行列式和矩阵的区别四、参考书目同济大学数学系. 工程数学线性代数第六版. 高等教育

重构大学数学基础_week05_雅各比矩阵与雅各比行列式

这周来讲一下雅各比矩阵和雅各比行列式。多元函数的局部线性属性首先我们来回顾一下向量函数，就是我们输入一个向量，输出也是一个向量，我们假设现在有一个向量函数这个函数意思就是在说，我们在原来的平面上有一个向量(x,y),经过这个函数的变换后，他变成了向量(x+sin(y),y+sin(x))，很明显，这个变换是非线性的，原来的平面会扭曲成下面这个样子但是这个函数变换有一个比较简

矩阵---A的行列式的值与A的转置的行列式的值是一致的

假设对A逐次进行行变换这也就相对于A的转置来说,逐次进行相应的列变换这也就意味着,A的行列式与A的转置的行列式,他们的值,都是一致的只不过我们是将他们横着看,还是竖着来看的问题

蓝桥杯练习系统（算法训练）ALGO-932 低阶行列式计算

资源限制内存限制：64.0MB C/C++时间限制：1.0s Java时间限制：3.0s Python时间限制：5.0s 问题描述　　给出一个n阶行列式(1<=n<=9)，求出它的值。输入格式　　第一行给出两个正整数n,p；　　接下来n行，每行n个数，表示行列式，数据保证行列式中每个数绝对值不超过2*10^9。输出格式　　一个数表示行列式的值，答案对p取余(

原本是为了编程实现线性回归的，想想，里面太多矩阵操作，尤其是求逆。以前学数值分析时，也用到过列主元高斯消去求解线性方程组，LU分解求解线性方程组。这次，同样是用高斯消去法求矩阵行列式的值，用LU分解求解矩阵的逆，效率上程序执行起来还行，比用python跑一边速度快，结果一致，这也潜在说明python库中矩阵求逆的实现应该也是用的LU分解。至于矩阵的其他一些操作，基本上算简单，当然面的稀疏性矩阵的话

Octave行列式矩阵运算

Octave行列式矩阵运算 Octave计算行列式指令一步步计算行列式 Octave矩阵加法Octave矩阵乘法Octave矩阵转置Octave矩阵求秩Octave矩阵求逆仅供本人查阅 Octave 是一个开源的数值计算软件，主要用于数学计算、算法开发和数据可视化。它是 MATLAB 语言的一个兼容性很高的替代品，适合于教学、科研以及解决各种工程和数学问题。以下是关于

AI笔记: 数学基础之矩阵运算与行列式

方阵行列式 1 ) 简单的方阵行列式行列式是数学的一个函数，可以看做是几何空间中，一个线性变换对"面积"或"体积"的影响方阵行列式，n阶方阵A的行列式表示为 ∣ A ∣ |A| ∣A∣ 或者 det(A) 1×1的方阵，其行列式等于该元素本身. A = ( a

行列式求解

行列式给出一个矩阵求行列式。输入： 1 3 1 -2 -1 0 3 2 3 1 -1 思路：不能直接乘上上面行的倍数来消除本行对应元素。试试辗转相减法把。 (1,3)减去2倍(0,1)->(1,0) (5,3)减去0倍(3,5)减去1倍(2,3)减去1倍(1,2)减去2倍(0,1)->(1,0) 然后每次检查上面行的元素是否为0，然后换回来就行了 #in

线性代数基础3 行列式

行列式行列式其实在机器学习中用的并不多，一个矩阵必须是方阵，才能计算它的行列式行列式是把矩阵变成一个标量 import numpy as npA = np.array([[1,3],[2,5]])display(A)print('矩阵A的行列式是：\n',np.linalg.det(A))'''array([[1, 3],[2, 5]])矩阵A的行列式是：-1.0''' 行

2020ICPC·小米网络选拔赛第二场 Determinant（行列式）

题意：按照题目规则组成的矩阵，求行列式值。思路：流下了不会线代的泪水，虽然最后推出来了，但是签到题那么久不应该。按照行列式的性质可以有如下变化 1 2 3 4 5 + x 6 7 8 9 \begin{matrix} 1 & 2 & 3 \\ 4 & 5+x & 6 \\ 7 & 8 & 9 \end{matrix} 14725+x8369 => 1 2 3 4 5

一个行列式求导

一个行列式求导公式 d ∣ A ∣ d t = ∣ A ∣ t r ( A − 1 ∗ d A d t ) , A ∈ R n × n \frac{d|A|}{dt} = |A|tr(A^{-1}*\frac{dA}{dt}),\ A\in R^{n \times n} dtd∣A∣=∣A∣tr(A−1∗dtdA), A∈Rn×n 证明如下首先我们有 ∣ A ( a i j +

matlab编程之矩阵的行列式实例解析

什么是矩阵的行列式？？矩阵的前提条件是，行与列相等的矩阵才有行列式假设现在有一个3*3矩阵 a=[1,2,3;4,5,6;0,1,-1]; 1 2 3 4 5 6 0 1 -1 按照以上的计算方式 1*5*(-1)+2*6*0+3*4*1=7 3*5*0+2*4*(-1)+1*6*!=-2 7-(-2)=9 我们根据数学公式得到的行列式是9，我们现在运行代码看

Cells（2021牛客暑期多校训练营9 C，LGV引理 + 范德蒙德行列式 + NTT）

一、题目链接 Cells 二、题目大意在一个二维平面内，有 n n n 个起点 ( 0 , a i ) (0, a_i) (0,ai) 要走到对应的终点 ( i , 0 ) (i, 0) (i,0)，每次可以向下走或向左走，问不相交路径组的方案数. 1 ≤ n ≤ 5 × 1 0 5 , 0 ≤ a i ≤ 1 0 6 , a i < a i + 1 1 \leq n \leq

计算n阶行列式

之前被Binto点名做这题了，简单做了一下，主要体现核心算法。算法也很普通，按照一般方法来做。思路：把行列式化为上三角，再计算斜边上元素之积。分析：单纯地化上三角是不行的，要考虑到斜边上的元素有可能为0.所以，在做每一列之前，都要先检查斜边上的元素是否为0，若是，则往下找非0行再交换正行。此为一个函数。而计算的时候倒是相当简单。就是保存当前行首非0元素与那个斜边

c语言计算行列式

大一刚学了c和线性代数，尝试一下写个行列式求值程序 #include<stdio.h> #include<math.h>int main(){int det(int b[][10],int x); //定义求行列式函数int a[10][10]; //定义一个固定数组int n,i=0,j=0,l;printf("输入行列式阶数\n");scanf("%d",&n);printf("输入行

线性代数(基础篇)：Ch1.行列式 Ch2.矩阵

文章目录线性代数0：串联各章的等价条件第1章行列式1.行列式的定义(1)行列式的本质定义(2)行列式的逆序数法定义(3)行列式的按行按列展开定理 (第三种定义)1.余子式 M i j M_{ij} Mij2.代数余子式 A i j A_{ij} Aij3.行列式的按行(按列)展开定理 2.行列式的性质3.求行列式的公式4.基本行列式(1)主对角线行列式(2)副对角线行列式(3)拉

工程数学-线性代数-第六版-第一章—行列式学习笔记

目录一、第一章——行列式 §1 二阶与三阶行列式一、二元线性方程组与二阶行列式二、三阶行列式 §2 全排列和对换一、排列及其逆序数二、对换 §3 n阶行列式的定义 §4 行列式的性质 §5 行列式按行（列）展开二、习题一三、参考书目一、第一章——行列式 §1 二阶与

0105行列式按行(列)展开-行列式-线性代数

在n阶行列式中，把 ( i , j ) 元 a i j (i,j)元a_{ij} (i,j)元aij所在的第 i 行和第 j i行和第j i行和第j列划去后，留下来的 n − 1 n-1 n−1阶行列式叫做 ( i , j ) 元 a i j (i,j)元a_{ij} (i,j)元aij的余子式，记作 M i j M_{ij} Mij；记 A i j = ( − 1 ) i + j M i