本文主要是介绍线性代数(基础篇):Ch1.行列式 Ch2.矩阵,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 线性代数
- 0:串联各章的等价条件
- 第1章 行列式
- 1.行列式的定义
- (1)行列式的本质定义
- (2)行列式的逆序数法定义
- (3)行列式的按行按列展开定理 (第三种定义)
- 1.余子式 M i j M_{ij} Mij
- 2.代数余子式 A i j A_{ij} Aij
- 3.行列式的按行(按列)展开定理
- 2.行列式的性质
- 3.求行列式的公式
- 4.基本行列式
- (1)主对角线行列式
- (2)副对角线行列式
- (3)拉普拉斯行列式 (分块矩阵的行列式)
- ①拉普拉斯行列式(主对角线)
- ②拉普拉斯行列式(副对角线)
- (4)范德蒙德行列式
- (5)爪型行列式
- (6)三对角行列式(异爪形行列式):递推公式
- (7)行和相等 (列和相等)
- 5.求行列式例题
- (1)具体行列式
- (2)抽象行列式
- 第2章 矩阵
- 1.矩阵的定义
- 方阵
- 2.矩阵运算
- (4)矩阵乘法
- (6)向量的内积与正交
- (7)施密特正交化
- (8)矩阵的幂
- 3.几种重要矩阵(几种特殊矩阵)
- 4.对角阵
- (1)对角阵的幂:主对角线上元素各取幂
- (2)对角阵的逆
- 8.正交矩阵
- 9.分块矩阵
- 16.秩一矩阵
- 4.可逆矩阵
- 5.伴随矩阵 A*
- (1)伴随矩阵的定义
- (2)伴随矩阵性质 (伴随矩阵公式)
- (3)求伴随矩阵
- 6.初等变换 与 初等矩阵
- (1)三种初等变换
- (2)初等变换性质
- (3)初等矩阵
- (4)初等矩阵的性质
- (5)左行右列定理:左乘行变换,右乘列变换
- 7.矩阵的秩
- (1)矩阵的秩的定义
- (2)秩的性质
- 8.等价矩阵、等价标准型
线性代数
0:串联各章的等价条件
1. A可逆
⇦⇨①|A|≠0
⇦⇨②r(A)=n,A满秩
⇦⇨③A的列向量 α₁,α₂,…αn线性无关
⇦⇨④Ax=0仅有零解 (系数矩阵的秩 = 列数,列满秩)
⇦⇨⑤A的特征值均不为0 【17年5.】
2. A不可逆
⇦⇨①|A|=0
⇦⇨②r(A)<n,A不满秩
⇦⇨③A的列向量 α₁,α₂,…αn线性相关
⇦⇨④Ax=0有非零解 (系数矩阵的秩 < 列数,列不满秩)
⇦⇨⑤A有0特征值
例题1:24李林六(六)5.
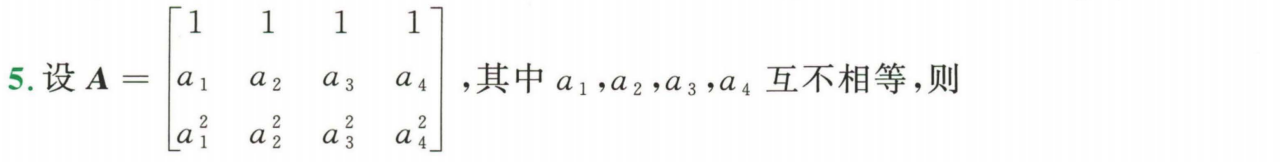

分析:
①取A前三列,为3阶范德蒙德行列式,值为 ( a 2 − a 1 ) ( a 3 − a 1 ) ( a 3 − a 2 ) ≠ 0 (a_2-a_1)(a_3-a_1)(a_3-a_2)≠0 (a2−a1)(a3−a1)(a3−a2)=0 (ai互不相等)。故 A 3 × 4 A_{3×4} A3×4有3阶子式不为0, r ( A ) = 3 r(A)=3 r(A)=3
② A 3 × 4 A_{3×4} A3×4, A 4 × 3 T A^T_{4×3} A4×3T,则 r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) = 3 < 4 r(A)=r(A^T)=r(AA^T)=r(A^TA)=3<4 r(A)=r(AT)=r(AAT)=r(ATA)=3<4
③ A X = 0 : { 仅有零解 ⇔ A 列满秩 有非零解 ⇔ A 列不满秩 AX=0:\left\{\begin{aligned} 仅有零解 &\Leftrightarrow A列满秩 \\ 有非零解 &\Leftrightarrow A列不满秩 \end{aligned}\right. AX=0:{仅有零解有非零解⇔A列满秩⇔A列不满秩
D. A T A 4 × 4 A^TA_{4×4} ATA4×4 列不满秩, A T A X = 0 A^TAX=0 ATAX=0有非零解。D✔
答案:D
第1章 行列式
1.行列式的定义
(1)行列式的本质定义
二阶行列式是以两个向量为邻边的平行四边形的面积,三阶行列式是以三个向量为邻边的平行六面体的体积,n阶行列式是以n个向量为邻边的n位图形的体积。
所以,读者应有这样的观点:把行列式看作是由若干个向量拼成的。
行列式的值非0时,具体是多少,只是量的问题。行列式的值是否为0,是一个质的问题。
例:①D₃≠0,则体积不为0,3个向量线性无关。若D₃=0,则3个向量线性相关。
②Dn≠0,n个向量线性无关。Dn=0,n个向量线性相关。
(2)行列式的逆序数法定义
1.排列和逆序

2.n阶行列式定义 (逆序数法)
【注意,行下标要顺排。求列标的逆序数,确定正负号】


举例1:
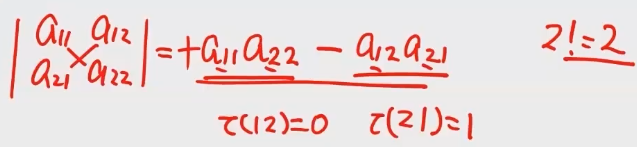
举例2:行列式的逆序数定义是“对角线法则”的由来。对角线法则只适用于二阶与三阶行列式。

例题1:

(3)行列式的按行按列展开定理 (第三种定义)
1.余子式 M i j M_{ij} Mij
去掉 a i j a_{ij} aij所在的第i行、第j列元素,余下元素组成的n-1阶子行列式,称为 a i j a_{ij} aij的余子式,记作 M i j M_{ij} Mij

2.代数余子式 A i j A_{ij} Aij
(1)代数余子式的定义: A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
(2)代数余子式的应用:
①代数余子式在同一行(列):求行列式或改写行列式
Ⅰ.求行列式:行列展开
Ⅱ.改写行列式:系数代替
②伴随矩阵: A ∗ = ( A i j ) T A^*=(A_{ij})^T A∗=(Aij)T
③ A 11 ≠ 0 A_{11}≠0 A11=0:
① r ( A ) ≥ n − 1 r(A)≥n-1 r(A)≥n−1。 [又|A|=0,∴r(A)=n-1,r(A*)=1,A*x=0有n-1个基础解系。]
② α 2 , α 3 , . . . , α n α_2,α_3,...,α_n α2,α3,...,αn线性无关。 [ A 11 = M 11 A_{11}=M_{11} A11=M11,即去掉第一行第一列剩下的n-1阶子式,行列式不为0,则线性无关。低维无关,则高维无关。]
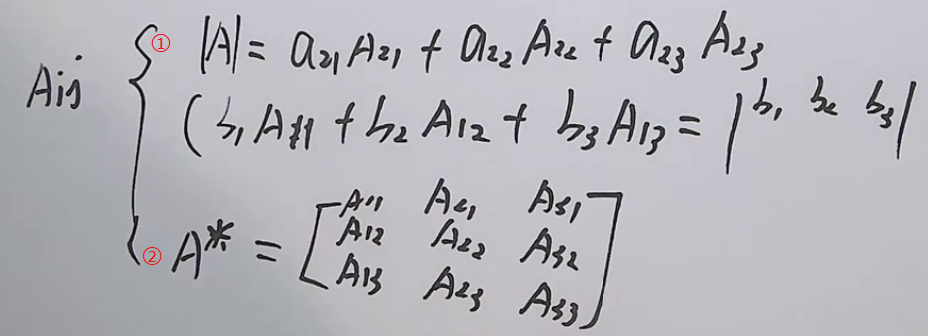

3.行列式的按行(按列)展开定理
行列式的按行(按列)展开定理:
(1) 行列式等于它的任一行(列)的各元素与其对应的代数余子式的乘积之和,即
D = a i 1 A i 1 + a i 2 A i 2 + . . . + a i n A i n ( i = 1 , 2 , . . , n ) D = a 1 j A 1 j + a 2 j A 2 j + . . . + a n j A n j ( j = 1 , 2 , . . , n ) D=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in}(i=1,2,..,n)\\[5mm] D=a_{1j}A_{1j}+a_{2j}A_{2j}+...+a_{nj}A_{nj}(j=1,2,..,n) D=ai1Ai1+ai2Ai2+...+ainAin(i=1,2,..,n)D=a1jA1j+a2jA2j+...+anjAnj(j=1,2,..,n)
(2)但行列式的某行(列)元素分别乘另一行(列)元素的代数余子式后再求和,结果为零,即
a i 1 A k 1 + a i 2 A k 2 + . . . + a i n A k n = 0 , i ≠ k a 1 j A 1 k + a 2 j A 2 k + . . . + a n j A n k = 0 , j ≠ k a_{i1}A_{k1}+a_{i2}A_{k2}+...+a_{in}A_{kn}=0,i≠k\\[5mm] a_{1j}A_{1k}+a_{2j}A_{2k}+...+a_{nj}A_{nk}=0,j≠k ai1Ak1+ai2Ak2+...+ainAkn=0,i=ka1jA1k+a2jA2k+...+anjAnk=0,j=k
不同行的元素与余子式相乘为0: ∑ k = 1 n a i k A j k = 0 ( i ≠ j ) \sum\limits_{k=1}^na_{ik}A_{jk}=0 \qquad (i≠j) k=1∑naikAjk=0(i=j)
2.行列式的性质
1.行列互换,其值不变: ∣ A ∣ = ∣ A T ∣ |A|=|A^T| ∣A∣=∣AT∣ 【行列地位等价】
2.行列式中 某行(列)元素全为0,则行列式值为0
3.若行列式某一行有公因子k,则可以提到行列式的外面 【倍乘】
4.行列式中某行元素均是两个元素之和,则可拆成两个行列式之和。反之,可相加。 (单行可拆性、单列可加性)
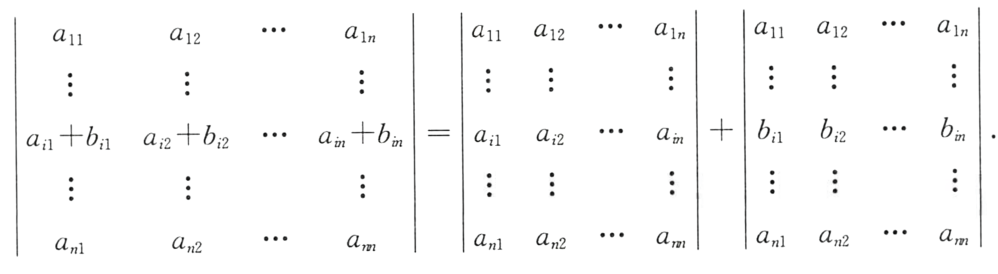
5.行列式中 两行(列)互换,行列式值反号
6.行列式中 两行元素相等或对应成比例,则行列式值为0
7.某行乘k倍加到另一行,行列式值不变 【倍加】
3.求行列式的公式
1. ∣ A B ∣ = ∣ A ∣ ⋅ ∣ B ∣ |AB|=|A|·|B| ∣AB∣=∣A∣⋅∣B∣ (A B为同阶方阵)
推论: ∣ A n ∣ = ∣ A ∣ n |A^n|=|A|^n ∣An∣=∣A∣n
2.若A为n阶方阵,则 ∣ k A ∣ = k n ∣ A ∣ |kA|=k^n|A| ∣kA∣=kn∣A∣
3. ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*|=|A|^{n-1} ∣A∗∣=∣A∣n−1
4.不满秩、不可逆、向量组线性相关,则行列式 = 0 满秩、可逆、行列式非零、线性无关的关系
5.一般地, ∣ A + B ∣ ≠ ∣ A ∣ + ∣ B ∣ |A+B|≠|A|+|B| ∣A+B∣=∣A∣+∣B∣
( A + B ) − 1 ≠ A − 1 + B − 1 (A+B)^{-1}≠A^{-1}+B^{-1} (A+B)−1=A−1+B−1
4.基本行列式
(1)主对角线行列式
右上三角行列式、左下三角行列式、对角行列式:主对角线元素的乘积
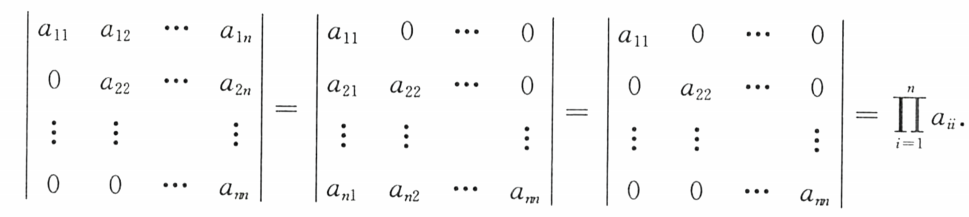
(2)副对角线行列式
逆序数 τ ( n , n − 1 , n − 2 , . . . 1 ) = ( n − 1 ) + ( n − 2 ) + . . . + 1 = n ( n − 1 ) 2 τ(n,n-1,n-2,...1)=(n-1)+(n-2)+...+1=\dfrac{n(n-1)}{2} τ(n,n−1,n−2,...1)=(n−1)+(n−2)+...+1=2n(n−1)

(3)拉普拉斯行列式 (分块矩阵的行列式)
①拉普拉斯行列式(主对角线)
∣ A O O B ∣ = ∣ A C O B ∣ = ∣ A O C B ∣ = ∣ A ∣ ∣ B ∣ \left|\begin{array}{cc} A & O \\ O & B \end{array}\right|=\left|\begin{array}{cc} A & C \\ O & B \end{array}\right|=\left|\begin{array}{cc} A & O \\ C & B \end{array}\right|=|A||B| AOOB = AOCB = ACOB =∣A∣∣B∣
②拉普拉斯行列式(副对角线)
∣ O A B O ∣ = ∣ C A B O ∣ = ∣ O A B C ∣ = ( − 1 ) m n ∣ A ∣ ∣ B ∣ \left|\begin{array}{cc} O & A \\ B & O \end{array}\right|=\left|\begin{array}{cc} C & A \\ B & O \end{array}\right|=\left|\begin{array}{cc} O & A \\ B & C \end{array}\right|=(-1)^{mn}|A||B| OBAO = CBAO = OBAC =(−1)mn∣A∣∣B∣ 【A为m阶矩阵,B为n阶矩阵】
(4)范德蒙德行列式
1.求值:只需看第二行,所有大的下标减去小的下标,然后连乘。
2.若 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn互不相等,则范德蒙德行列式≠0
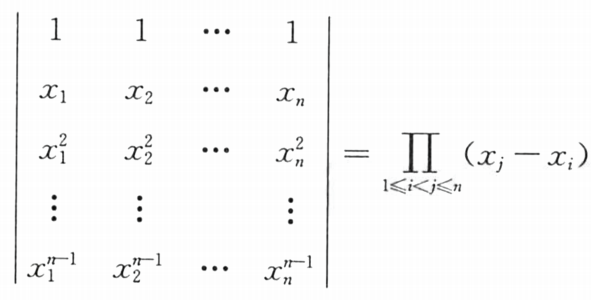
(5)爪型行列式
斜爪 消 平(竖)爪,化为三角行列式
(6)三对角行列式(异爪形行列式):递推公式
喻老方法:
草纸上写5阶,找到 D 5 D_5 D5的规律,类比得出 D n D_n Dn的规律,推到 D 1 D_1 D1。然后求出 D n D_n Dn
例题:880 行列式基础解答3
张宇方法:
(1)阶数不高:直接展开 ①凑0最多 ②按展开后基本型最多(三角行列式最多)的方式展开
(2)阶数较高,n阶:递推法

(1)递推法:建立 D n D_n Dn 与 D n − 1 D_{n-1} Dn−1 的关系式,从而实现递推。
①元素分布规律相同
② D n − 1 D_{n-1} Dn−1只比 D n D_n Dn 少一阶
(2)展开方法
①三对角行列式方法:所有的行加到最后一行 (所有列加到第一列),然后展开。观察负号。
②两斜一横(竖):对爪尾的两个尖尖进行展开,找递推规律
(7)行和相等 (列和相等)
1.行和相等的矩阵的性质:(以三阶矩阵A为例,每行元素之和均为k)
行和k 是A的一个特征值, ( 1 1 1 ) \left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right) 111 是对应 行和k 的一个特征向量
2.计算行列式:全部加到第一列,提取公因式,第一列全为1。
再将第一列下方全消为0,按照第一列展开。
5.求行列式例题
(1)具体行列式
例题1:计算行列式
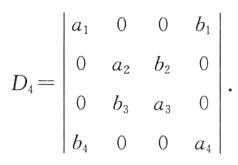
分析:凑分块矩阵、零矩阵。将13列互换,再将24行互换
答案: ( a 1 a 4 − b 1 b 4 ) ( a 2 a 3 − b 2 b 3 ) (a_1a_4-b_1b_4)(a_2a_3-b_2b_3) (a1a4−b1b4)(a2a3−b2b3)
例题2:低阶

分析:异爪型行列式,按照最后一行展开。发现余子式均为主对角线行列式
答案: λ 4 + λ 3 + 2 λ 2 + 3 λ + 4 λ^4+λ^3+2λ^2+3λ+4 λ4+λ3+2λ2+3λ+4
例题3:

答案:

例题4:15年13. 求n阶异爪型行列式
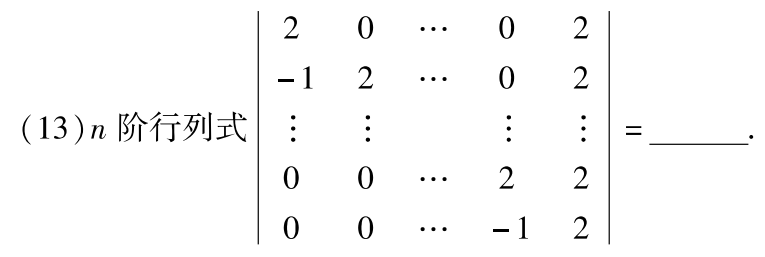
分析:异爪型行列式,按照爪尾的两个尖尖展开,找递推规律

答案: 2 n + 1 − 2 2^{n+1}-2 2n+1−2
例题5:
(1)主对角线

分析:行和相等,为 a+(n-1)b
答案:

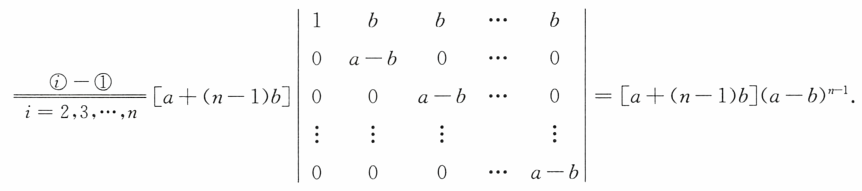
(2)副对角线

(2)抽象行列式
例题1:24李林四(三)15. 行列式的性质、可逆矩阵
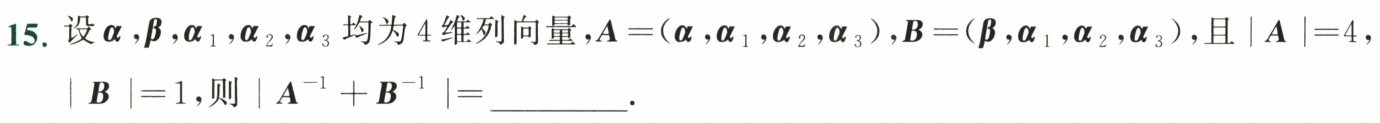
分析:
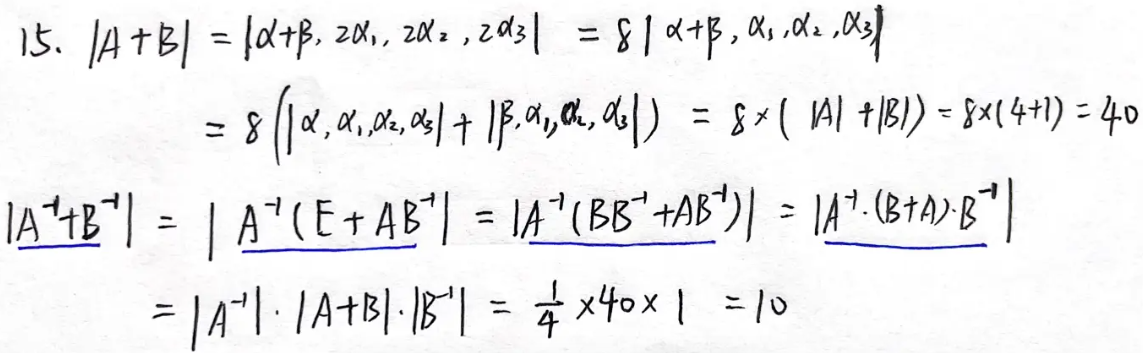
答案:10
例题2:24李林四(一)15. 可逆矩阵的定义
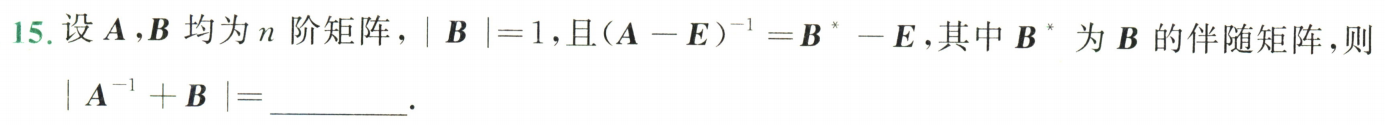
分析:
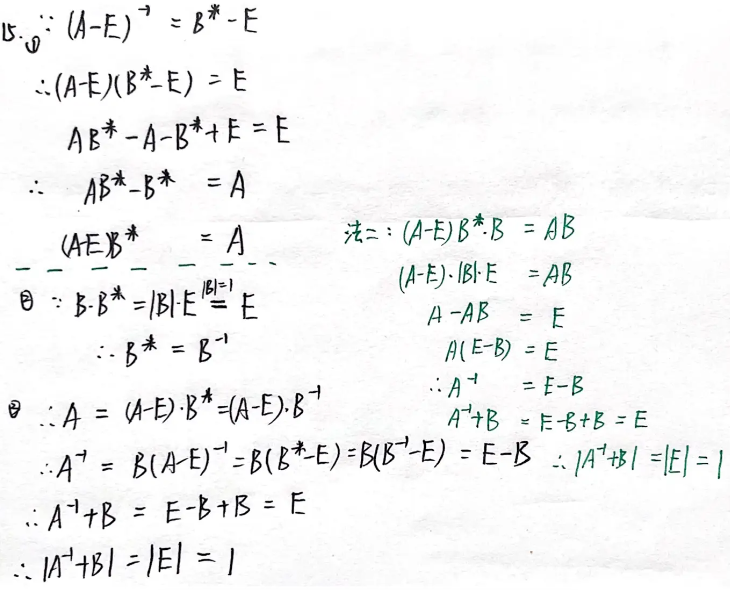
答案:1
例题3:23李林四(三)15. 可逆矩阵的定义
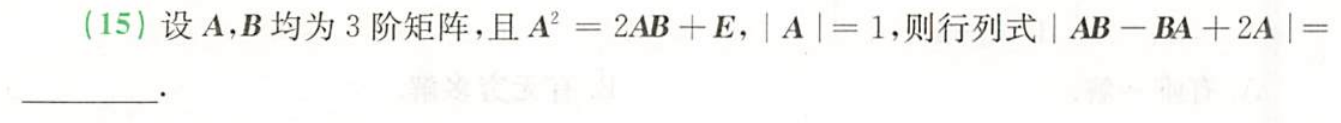
分析:
凑可逆阵:由 A 2 = 2 A B + E A²=2AB+E A2=2AB+E,移项得 A 2 − 2 A B = E A²-2AB=E A2−2AB=E,即 A ( A − 2 B ) = E A(A-2B)=E A(A−2B)=E。
∴ A A A与 A − 2 B A-2B A−2B互为可逆阵,∴ A ( A − 2 B ) = ( A − 2 B ) A = E A(A-2B)=(A-2B)A=E A(A−2B)=(A−2B)A=E,即 A 2 − 2 A B = A 2 − 2 B A A²-2AB=A²-2BA A2−2AB=A2−2BA。即 A B = B A AB=BA AB=BA。
∴ ∣ A B − B A + 2 A ∣ = ∣ 2 A ∣ = 2 3 ∣ A ∣ = 8 × 1 = 8 |AB-BA+2A|=|2A|=2³|A|=8×1=8 ∣AB−BA+2A∣=∣2A∣=23∣A∣=8×1=8
答案:8
例题4:24李林六(五)15、23李林四(一)15.
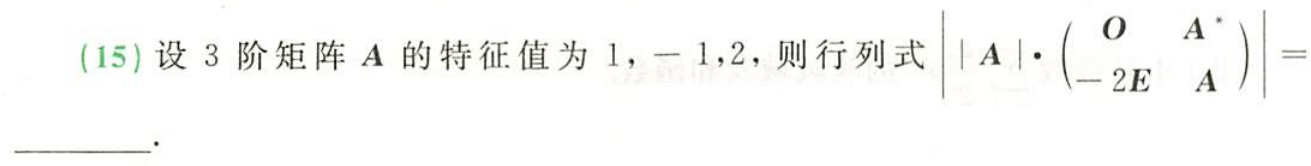
分析: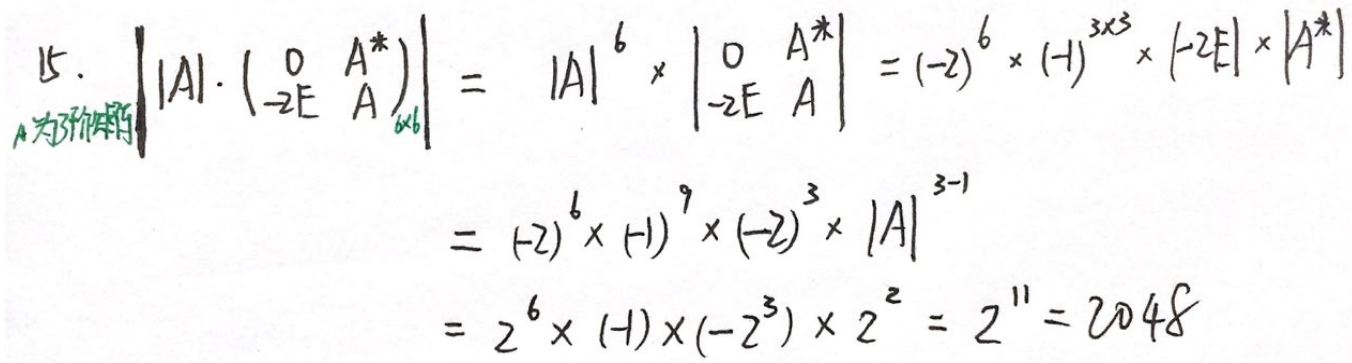
答案:2048
例题5:24李林六(四)15.

分析:

答案:8
例题6:21年15.

分析:

答案: 3 2 \dfrac{3}{2} 23
例题7:将向量的线性组合 表示为 矩阵相乘的形式
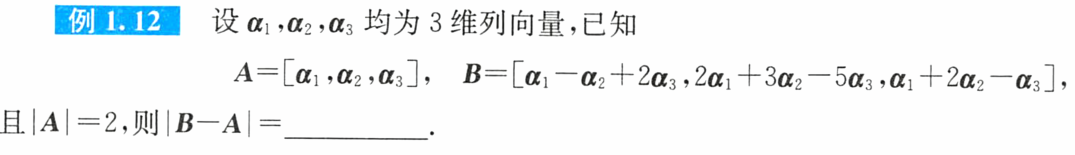
分析:
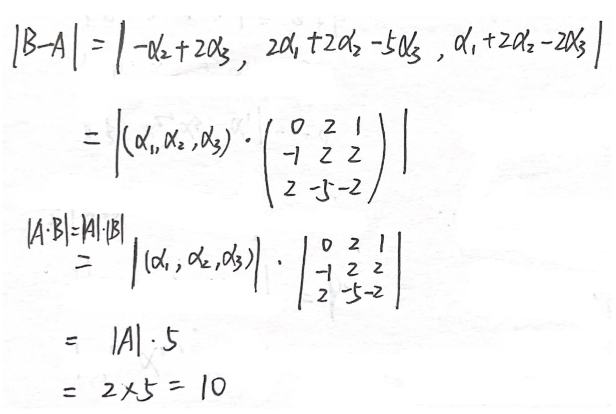
答案:10
例题8:
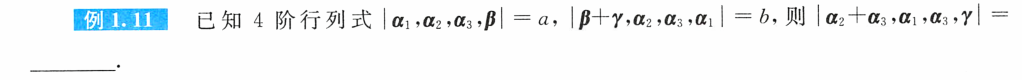
分析:从右向左,化简目标,凑成已知
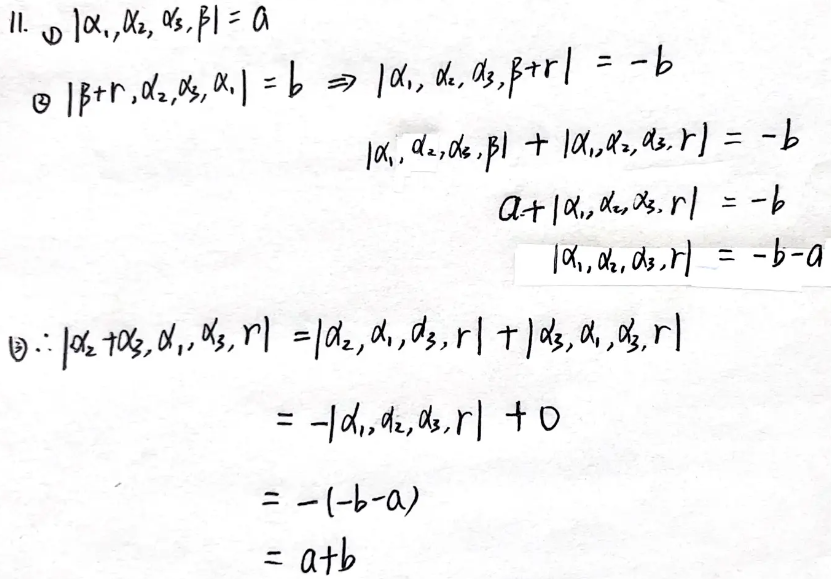
答案:a+b
第2章 矩阵
1.矩阵的定义
1.矩阵:
矩阵本身是一个数表,不进行运算。矩阵由若干个向量组成。
①m×n矩阵 ②n阶方阵 (n阶矩阵,即为n×n矩阵)
2.同型矩阵:
行数相同,列数也相同


方阵
1.方阵定义:
方阵为行列数相等的矩阵,如Ann、Amm
2.只有方阵才有的性质:
(1)行列式
只有方阵才有行列式。
别再问汤家凤老师3行4列的行列式怎么算了。“你有没有发现把我吓死了”(doge)
(2)逆矩阵
1.可逆矩阵一定是方阵。
2.如果矩阵A是可逆的,其逆矩阵是唯一的。
(3)特征值、特征向量
只有方阵才有特征值与特征向量
(4)二次型
只有方阵才有二次型

2.矩阵运算
五大矩阵运算:①求行列式 ②求转置 ③求逆 ④求伴随 ⑤求幂

(1)相等
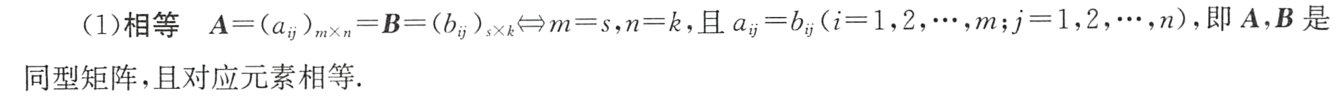
(2)加法

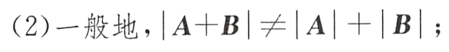
(3)数乘矩阵
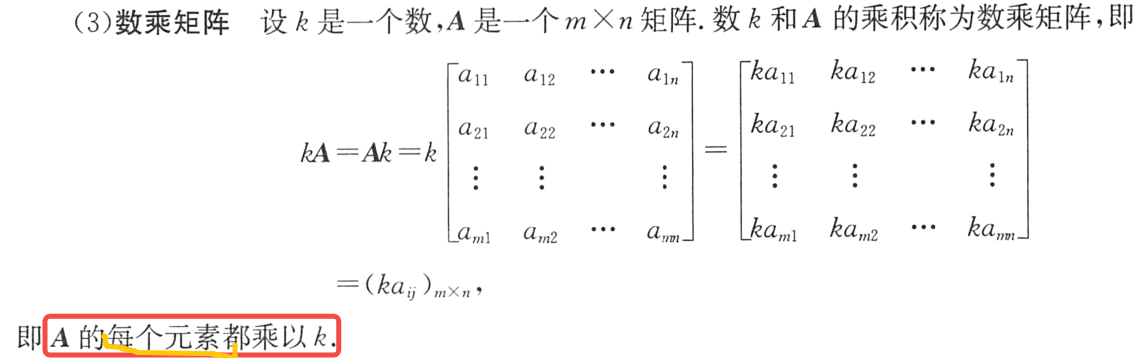
(4)矩阵乘法
c i j c_{ij} cij为 a i a_i ai和 b j b_j bj两向量的内积:
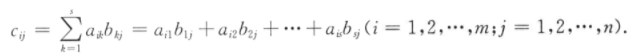
注:矩阵乘法,只满足结合律,不满足交换律、消去律
(Ⅰ)矩阵乘法一般情况下不满足交换律,不能随意交换位置,即 A B ≠ B A AB≠BA AB=BA
故:① ( A B ) 2 ≠ A 2 B 2 (AB)^2≠A^2B^2 (AB)2=A2B2,正确的写法应该是 ( A B ) 2 = A B A B ≠ A A B B (AB)^2=ABAB≠AABB (AB)2=ABAB=AABB
② ( A + B ) 2 ≠ A 2 + 2 A B + B 2 (A+B)^2≠A^2+2AB+B^2 (A+B)2=A2+2AB+B2,正确的写法应该是 ( A + B ) 2 = ( A + B ) ( A + B ) = A 2 + A B + B A + B 2 (A+B)^2=(A+B)(A+B)=A^2+AB+BA+B^2 (A+B)2=(A+B)(A+B)=A2+AB+BA+B2
(Ⅱ)矩阵乘法一般情况下也不满足消去律:
①AB=O推不出A=O或B=O
②AB=AC,A(B-C)=O,即使A≠O,也推不出B=C
【19年5.】
反例: ( 1 0 0 0 ) ( 0 0 1 0 ) = ( 0 0 0 0 ) \left(\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right)=\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right) (1000)(0100)=(0000)

(5)转置、转置矩阵
①若A为方阵, ∣ A ∣ = ∣ A T ∣ |A|=|A^T| ∣A∣=∣AT∣
② ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
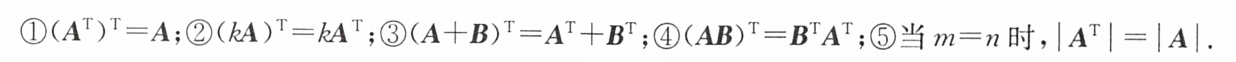
转置T:transpose、transposition
(6)向量的内积与正交
内积: ( α , β ) = α T β (α,β)=α^Tβ (α,β)=αTβ
正交: α T β = 0 α^Tβ=0 αTβ=0

例题:
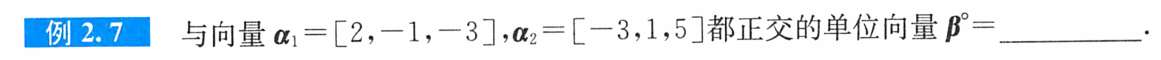
答案:

(7)施密特正交化
β 1 = α 1 β₁=α₁ β1=α1
β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 β₂=α₂-\dfrac{(α₂,β₁)}{(β₁,β₁)}β₁ β2=α2−(β1,β1)(α2,β1)β1
β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 β₃=α₃-\dfrac{(α₃,β₁)}{(β₁,β₁)}β₁-\dfrac{(α₃,β₂)}{(β₂,β₂)}β₂ β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2
…
β n = α n − ( α n , β 1 ) ( β 1 , β 1 ) β 1 − ( α n , β 2 ) ( β 2 , β 2 ) β 2 − . . . − ( α n , β n − 1 ) ( β n − 1 , β n − 1 ) β n − 1 β_n=α_n-\dfrac{(α_n,β₁)}{(β₁,β₁)}β₁-\dfrac{(α_n,β₂)}{(β₂,β₂)}β₂-...-\dfrac{(α_n,β_{n-1})}{(β_{n-1},β_{n-1})}β_{n-1} βn=αn−(β1,β1)(αn,β1)β1−(β2,β2)(αn,β2)β2−...−(βn−1,βn−1)(αn,βn−1)βn−1

例题1:
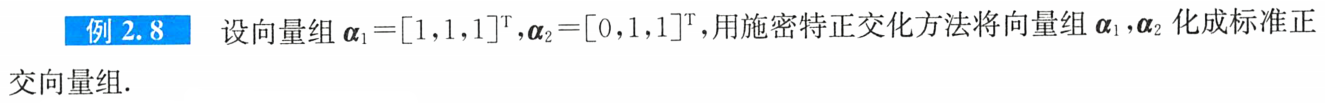
答案:
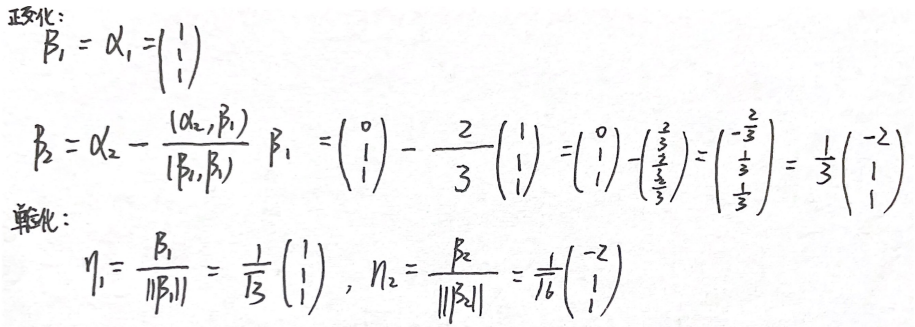
例题2:21年6. 施密特正交化
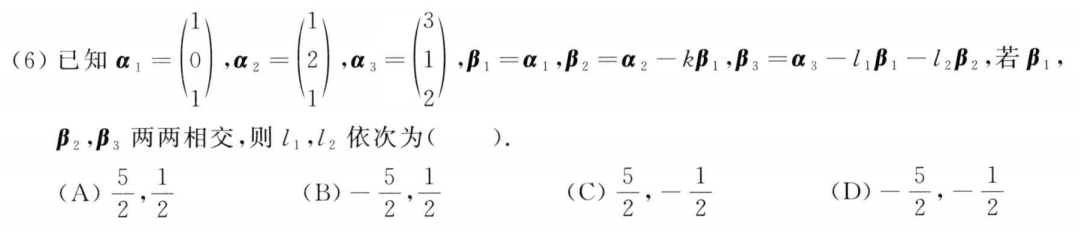
分析:
k = 1 , β 2 = ( 0 , 2 , 0 ) T k=1,β_2=(0,2,0)^T k=1,β2=(0,2,0)T
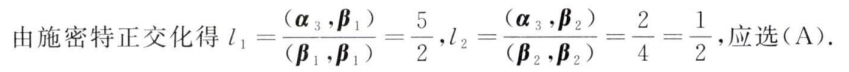
答案:A
(8)矩阵的幂
5种方法求矩阵的幂An:
①找规律:
试算A2、A3,归纳An
②秩为1的方阵:
若 r ( A ) = 1 r(A)=1 r(A)=1,则 A n = [ t r ( A ) ] n − 1 ⋅ A A^n=[tr(A)]^{n-1}·A An=[tr(A)]n−1⋅A
A = α ⋅ β T A=α·β^T A=α⋅βT, β T β^T βT为第一行,列向量 α α α为各行的系数
【若 r ( A ) = 1 r(A)=1 r(A)=1,则n个特征值中,一个特征值为tr(A),剩余n-1个特征值均为0】

③幂零矩阵 (主对角线元素为0):
A = B + k E A = B+kE A=B+kE:二次展开式, A n = ( B + k E ) n A^n = (B+kE)^n An=(B+kE)n
【A = B+C,An = (B+C)n。要求BC=CB,可用二项展开式 。一般令C=kE】
④A可相似可角化:
若 P − 1 A P = Λ P^{-1}AP=Λ P−1AP=Λ,则 A = P Λ P − 1 A=PΛP^{-1} A=PΛP−1, A n = P Λ n P − 1 A^n=PΛ^nP^{-1} An=PΛnP−1
步骤:
1>用 ∣ λ E − A ∣ = 0 |λE-A|=0 ∣λE−A∣=0 求出A的特征值和特征向量
2>用特征值组成 Λ Λ Λ,用特征向量组成 P P P
3>验证A可相似对角化,则: P − 1 A P = Λ P^{-1}AP=Λ P−1AP=Λ,则 A = P Λ P − 1 A=PΛP^{-1} A=PΛP−1,则 A n = P Λ n P − 1 A^n=PΛ^nP^{-1} An=PΛnP−1
⑤分块矩阵,分块分别求n次幂:
A = [ B O O C ] A=\left[\begin{array}{cc} B & O \\ O & C \end{array}\right] A=[BOOC],则 A n = [ B n O O C n ] A^n=\left[\begin{array}{cc} B^n & O \\ O & C^n \end{array}\right] An=[BnOOCn]
例题1:2016年21. A可相似对角化
例题2:试算,归纳
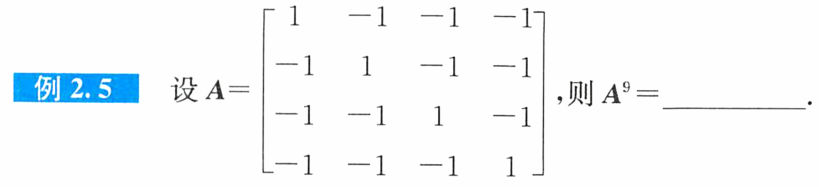
答案:
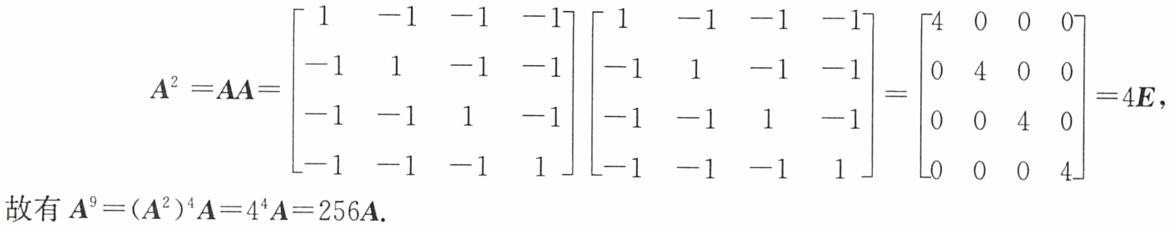
例题3: A n = ( B + C ) n A^n=(B+C)^n An=(B+C)n

答案:
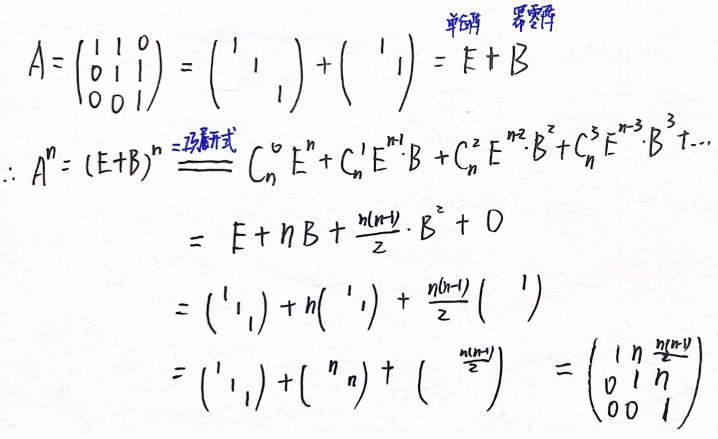
例题4:张宇30讲线代分册 分块矩阵
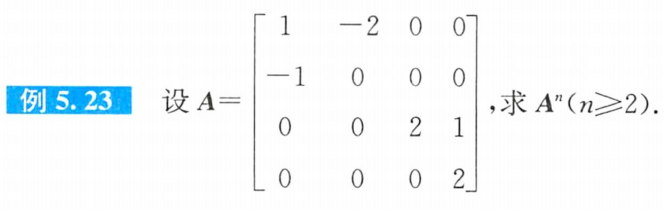
答案:

例题5:23李林四(一)23.

答案:

3.几种重要矩阵(几种特殊矩阵)
1.零矩阵:O
2.单位矩阵:E
性质:E为n阶矩阵,无论n为几,都有 ∣ E ∣ = 1 |E|=1 ∣E∣=1
3.数量矩阵:kE
4.对角阵
Λ = d i a g ( λ 1 , λ 2 , . . . , λ n ) = ( λ 1 λ 2 . . . λ n ) Λ={\rm diag}(λ₁,λ₂,...,λ_n)=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ & & & λ_n \end{array}\right) Λ=diag(λ1,λ2,...,λn)= λ1λ2...λn
(1)对角阵的幂:主对角线上元素各取幂
Λ n = ( λ 1 n λ 2 n . . . λ n n ) Λ^n=\left(\begin{array}{cc} {λ₁}^n & & \\ & {λ₂}^n & \\ & & ...\\ & & & {λ_n}^n \end{array}\right) Λn= λ1nλ2n...λnn
(2)对角阵的逆
对角阵的逆矩阵:主对角线上元素都取倒数。【即对角阵的幂取 n = -1】
Λ − 1 = ( λ 1 λ 2 λ 3 ) − 1 = ( 1 λ 1 1 λ 2 1 λ 3 ) Λ^{-1}=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & & λ_3 \end{array}\right)^{-1}=\left(\begin{array}{cc} \dfrac{1}{λ₁} & & \\ & \dfrac{1}{λ₂} & \\ & & & \dfrac{1}{λ_3} \end{array}\right) Λ−1= λ1λ2λ3 −1= λ11λ21λ31
5.上/下三角矩阵
上(下)三角矩阵和对角阵的特征值,均为主对角线元素
6.对称矩阵
A T = A ⇔ a i j = a j i A^T=A\Leftrightarrow a_{ij}=a_{ji} AT=A⇔aij=aji
若 a i j = A i j a_{ij}=A_{ij} aij=Aij,则 A T = A ∗ A^T=A^* AT=A∗
7.反对称矩阵
A T = − A ⇔ { a i j = − a j i , i ≠ j a i i = 0 A^T=-A \Leftrightarrow \left\{\begin{aligned} a_{ij}&=-a_{ji},i≠j \\ a_{ii}&=0 \end{aligned}\right. AT=−A⇔{aijaii=−aji,i=j=0
8.正交矩阵
定义: Q T Q = Q Q T = E Q^TQ=QQ^T=E QTQ=QQT=E
⇔ Q T = Q − 1 \Leftrightarrow Q^T=Q^{-1} ⇔QT=Q−1
⇔ \Leftrightarrow ⇔ Q Q Q是由标准正交基组成(两两垂直正交,且都是单位向量)
9.分块矩阵
性质:副对角线要对调位置
(1)分块矩阵的逆矩阵:
①对角阵
主对角线: ( A O O B ) − 1 = ( A − 1 O O B − 1 ) \left(\begin{array}{cc} A & O \\ O & B \end{array}\right)^{-1}=\left(\begin{array}{cc} A^{-1} & O \\ O & B^{-1} \end{array}\right) (AOOB)−1=(A−1OOB−1)
副对角线:
(1)求逆: ( O A B O ) − 1 = ( O B − 1 A − 1 O ) \left(\begin{array}{cc} O & A \\ B & O \end{array}\right)^{-1}=\left(\begin{array}{cc} O &B^{-1} \\ A^{-1} & O \end{array}\right) (OBAO)−1=(OA−1B−1O)
(2)行列式: ∣ O A B O ∣ = \left|\begin{array}{cc} O & A \\ B & O \end{array}\right|= OBAO =
②三角阵
左乘同行,右乘同列,取相反数
主对角线:
( A O C B ) − 1 = ( A − 1 O − B − 1 C A − 1 B − 1 ) \left(\begin{array}{cc} A & O \\ C & B \end{array}\right)^{-1}=\left(\begin{array}{cc} A^{-1} & O \\ -B^{-1}CA^{-1} & B^{-1} \end{array}\right) (ACOB)−1=(A−1−B−1CA−1OB−1)
( A C O B ) − 1 = ( A − 1 − A − 1 C B − 1 O B − 1 ) \left(\begin{array}{cc} A & C \\ O & B \end{array}\right)^{-1}=\left(\begin{array}{cc} A^{-1} & -A^{-1}CB^{-1} \\ O & B^{-1} \end{array}\right) (AOCB)−1=(A−1O−A−1CB−1B−1)
副对角线:
( O A B C ) − 1 = ( − B − 1 C A − 1 B − 1 A − 1 O ) \left(\begin{array}{cc} O & A \\ B & C \end{array}\right)^{-1}=\left(\begin{array}{cc} -B^{-1}CA^{-1} &B^{-1} \\ A^{-1} & O \end{array}\right) (OBAC)−1=(−B−1CA−1A−1B−1O)
( C A B O ) − 1 = ( O B − 1 A − 1 − A − 1 C B − 1 ) \left(\begin{array}{cc} C & A \\ B & O \end{array}\right)^{-1}=\left(\begin{array}{cc} O &B^{-1} \\ A^{-1} & -A^{-1}CB^{-1} \end{array}\right) (CBAO)−1=(OA−1B−1−A−1CB−1)
(2)分块矩阵的转置矩阵
主对角线: ( A O O B ) T = ( A T O O B T ) \left(\begin{array}{cc} A & O \\ O & B \end{array}\right)^T=\left(\begin{array}{cc} A^T & O \\ O & B^T \end{array}\right) (AOOB)T=(ATOOBT)
副对角线: ( O A B O ) T = ( O B T A T O ) \left(\begin{array}{cc} O & A \\ B & O \end{array}\right)^T=\left(\begin{array}{cc} O &B^T \\ A^T & O \end{array}\right) (OBAO)T=(OATBTO)
10.幂零矩阵: A k = O A^k=O Ak=O
①幂零矩阵的主对角线元素为0,每升一次幂,元素就向右上方移动一斜行,秩减一。
11.幂幺矩阵: A k = E A^k=E Ak=E
12.幂等矩阵: A 2 = A A^2=A A2=A
幂等矩阵一定可相似对角化 【880 相似矩阵 基础解答10(Ⅱ)】
13.行阶梯形矩阵
①若有零行,全在下方:所有非零行在所有零行的上面
②从行上看,出现连续0的个数自上而下严格单增:所有非零行的首个非零元所在列标严格单增
14.行最简形矩阵
①首先是行阶梯形矩阵
②每个非零行的首个非零元(主元)为1
③每个非零行的首个非零元所在列的其他元素均为0
15.标准形矩阵
左上角为单位矩阵,其他元素均为0

16.秩一矩阵
即秩为一的矩阵, r ( A ) = 1 r(A)=1 r(A)=1,性质:
1.
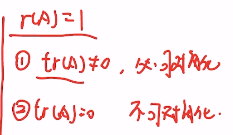
例题1:07年15. 幂零矩阵
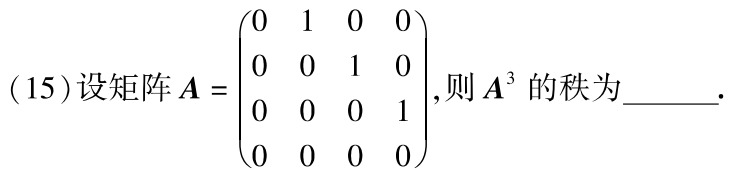
分析:A的秩为3,A²的秩为2,A³的秩为1,An=A4的秩为0

答案:1
例题2:08年5. (1)幂零阵 (2)可逆矩阵定义、立方和公式、立方差公式

分析:
法一:幂零矩阵,取特殊值
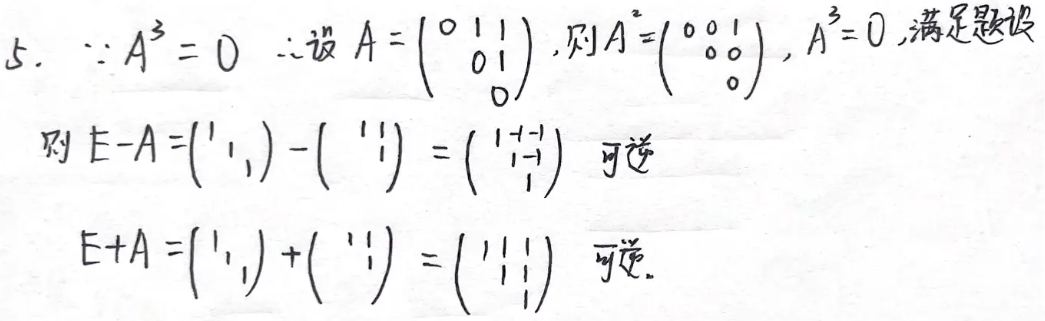
法二:可逆矩阵定义、立方和公式、立方差公式
由 A 3 = O A³=O A3=O得 E ± A 3 = E E±A^3=E E±A3=E
即 E = E + A 3 = ( E + A ) ( E 2 − A E + A 2 ) = ( E + A ) ( E − A + A 2 ) E=E+A^3=(E+A)(E^2-AE+A^2)=(E+A)(E-A+A²) E=E+A3=(E+A)(E2−AE+A2)=(E+A)(E−A+A2),则 E + A E+A E+A可逆且 ( E + A ) − 1 = E − A + A 2 (E+A)^{-1}=E-A+A² (E+A)−1=E−A+A2
即 E = E − A 3 = ( E − A ) ( E 2 + A E + A 2 ) = ( E − A ) ( E + A + A 2 ) E=E-A^3=(E-A)(E^2+AE+A^2)=(E-A)(E+A+A^2) E=E−A3=(E−A)(E2+AE+A2)=(E−A)(E+A+A2),则 E − A E-A E−A可逆且 ( E − A ) − 1 = E + A + A 2 (E-A)^{-1}=E+A+A^2 (E−A)−1=E+A+A2
答案:C
4.可逆矩阵
(1)可逆矩阵的定义
1.对于n阶方阵A,若存在一个n阶方阵B,使得 A B = E 或 B A = E AB=E\ 或\ BA=E AB=E 或 BA=E,则A、B互逆:
① A = B − 1 , B = A − 1 A=B^{-1},B=A^{-1} A=B−1,B=A−1
② A B = E = B A AB=E=BA AB=E=BA
2.特殊情况:若 A ( k B ) = E A(kB)=E A(kB)=E,则 k B kB kB为A的逆矩阵

例题1:22年15.
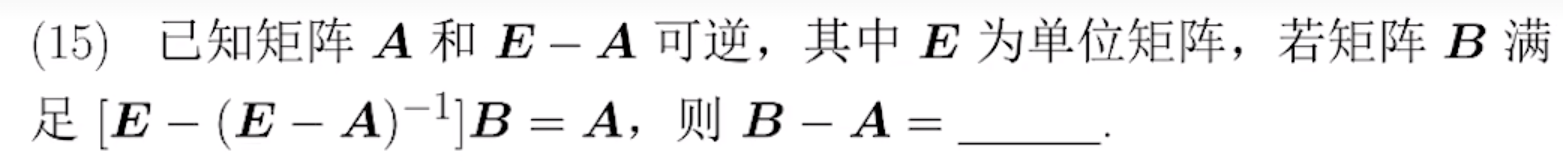
分析:可逆矩阵的定义
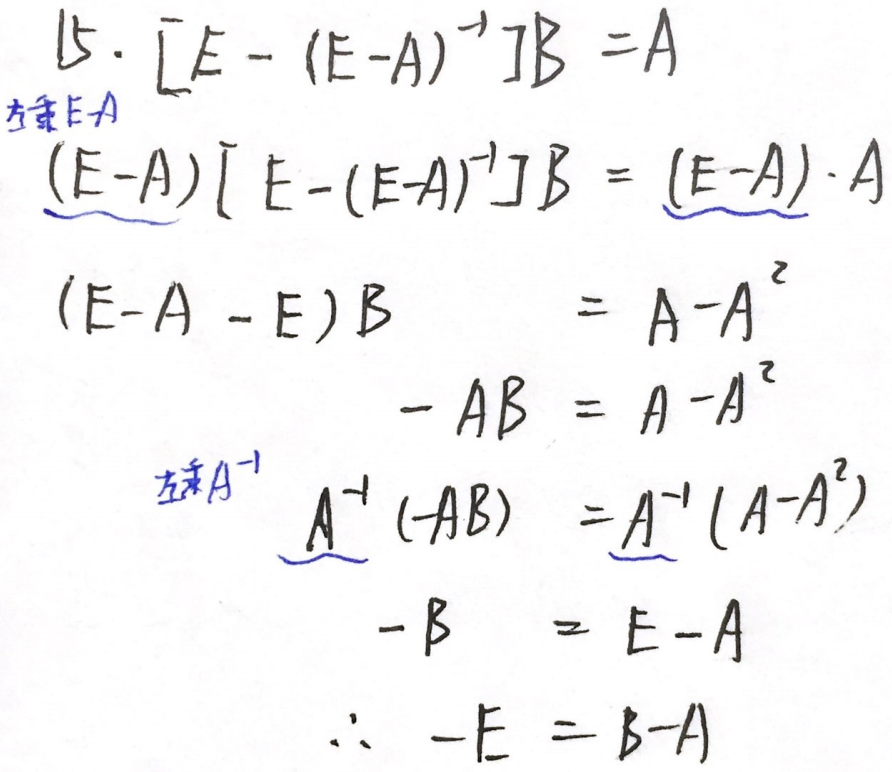
答案:-E
例题2:01年4.
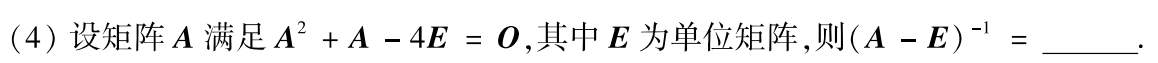
解:由 A 2 + A − 4 E = O A²+A-4E=O A2+A−4E=O,移项得 A 2 + A − 2 E = 2 E A²+A-2E=2E A2+A−2E=2E
得 ( A + 2 E ) ( A − E ) = 2 E (A+2E)(A-E)=2E (A+2E)(A−E)=2E ∴ ( A − E ) − 1 = 1 2 ( A + 2 E ) ∴(A-E)^{-1}=\dfrac{1}{2}(A+2E) ∴(A−E)−1=21(A+2E) 注意,系数要放在括号外,不要把矩阵写成分式
答案: 1 2 ( A + 2 E ) \dfrac{1}{2}(A+2E) 21(A+2E)
例题3:08年5. 幂零阵、可逆矩阵定义、立方和公式、立方差公式

① E 3 = E 3 + A 3 = ( E + A ) ( E 2 − A E + A 2 ) = ( E + A ) ( E − A + A 2 ) E^3=E^3+A^3=(E+A)(E^2-AE+A^2)=(E+A)(E-A+A²) E3=E3+A3=(E+A)(E2−AE+A2)=(E+A)(E−A+A2),则 E + A E+A E+A可逆且 ( E + A ) − 1 = E − A + A 2 (E+A)^{-1}=E-A+A² (E+A)−1=E−A+A2
② E 3 = E 3 − A 3 = ( E − A ) ( E 2 + A E + A 2 ) = ( E − A ) ( E + A + A 2 ) E^3=E^3-A^3=(E-A)(E^2+AE+A^2)=(E-A)(E+A+A^2) E3=E3−A3=(E−A)(E2+AE+A2)=(E−A)(E+A+A2),则 E − A E-A E−A可逆且 ( E − A ) − 1 = E + A + A 2 (E-A)^{-1}=E+A+A^2 (E−A)−1=E+A+A2
答案:C
例题4:

分析:
A B = A + B AB = A+B AB=A+B
A B − A − B = O AB -A-B=O AB−A−B=O
A ( B − E ) − B = O A(B-E)-B=O A(B−E)−B=O
A ( B − E ) − ( B − E ) = E A(B-E)-(B-E)=E A(B−E)−(B−E)=E
( A − E ) ( B − E ) = E (A-E)(B-E)=E (A−E)(B−E)=E
∴ A − E A-E A−E 与 B − E B-E B−E互为逆矩阵
答案:A
(2)可逆矩阵性质
若A为n阶可逆矩阵,则:
①A的逆矩阵必唯一
② ∣ A ∣ ≠ 0 |A|≠0 ∣A∣=0
③ A − 1 A^{-1} A−1也可逆,且 ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
A T A^T AT也可逆,且 ( A − 1 ) T = ( A T ) − 1 (A^{-1})^T=(A^T)^{-1} (A−1)T=(AT)−1
④乘可逆矩阵,不改变原矩阵的秩
⑤ ( k A ) − 1 = 1 k A − 1 ( k ≠ 0 ) (kA)^{-1}=\dfrac{1}{k}A^{-1} \ (k≠0) (kA)−1=k1A−1 (k=0)
⑥ ∣ A − 1 ∣ = ∣ A ∣ − 1 |A^{-1}|=|A|^{-1} ∣A−1∣=∣A∣−1
⑦若B也为n阶可逆矩阵,则 A B AB AB也可逆,且 ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
但 A + B A+B A+B不一定可逆,且 ( A + B ) − 1 ≠ A − 1 + B − 1 (A+B)^{-1}≠A^{-1}+B^{-1} (A+B)−1=A−1+B−1

例题1:17年13. 乘可逆矩阵,不改变原矩阵的秩

分析:
A = ( 1 0 1 1 1 2 0 1 1 ) → ( 1 0 1 0 1 1 0 0 0 ) A=\left(\begin{array}{cc} 1 & 0 & 1\\ 1 & 1 & 2\\ 0 & 1 & 1\\ \end{array}\right)→\left(\begin{array}{cc} 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 0 & 0\\ \end{array}\right) A= 110011121 → 100010110 ∴ r ( A ) = 2 ∴r(A)=2 ∴r(A)=2
矩阵 ( A α 1 , A α 2 , A α 3 ) = A ( α 1 , α 2 , α 3 ) (Aα_1,Aα_2,Aα_3)=A(α_1,α_2,α_3) (Aα1,Aα2,Aα3)=A(α1,α2,α3)
∵ α 1 , α 2 , α 3 α_1,α_2,α_3 α1,α2,α3线性无关 ∴ ( α 1 , α 2 , α 3 ) (α_1,α_2,α_3) (α1,α2,α3)为可逆矩阵
∴ r ( A α 1 , A α 2 , A α 3 ) = r ( A ) = 2 r(Aα_1,Aα_2,Aα_3)=r(A)=2 r(Aα1,Aα2,Aα3)=r(A)=2
答案:2
例题2:17年5.
(3)求逆矩阵
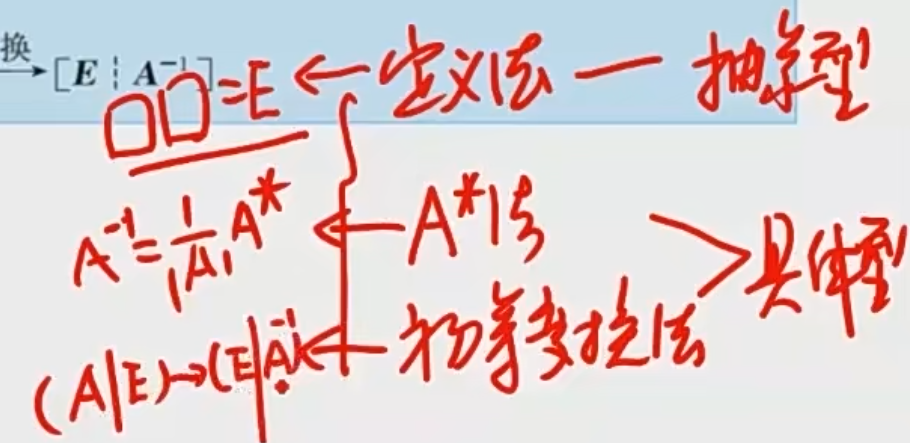
1.逆矩阵定义: ▯ ⋅ ▯ = E ▯·▯=E ▯⋅▯=E
A B = E AB=E AB=E,则 A − 1 = B A^{-1}=B A−1=B
2.用伴随矩阵求逆矩阵: A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\dfrac{1}{|A|}A^* A−1=∣A∣1A∗
求数值矩阵的逆矩阵,步骤:
①求|A|≠0
②求A*
③写出 A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\dfrac{1}{|A|}A^* A−1=∣A∣1A∗
注意,求 A ∗ A^* A∗ 的时候:① A ∗ A^* A∗和 A i j A_{ij} Aij的位置是竖着求的 ②注意负号 A i j = − ( 1 ) i + j M i j A_{ij}=-(1)^{i+j}M_{ij} Aij=−(1)i+jMij
3.初等变换法求逆矩阵: ( A ∣ E ) → ( E ∣ A − 1 ) (A|E)→(E|A^{-1}) (A∣E)→(E∣A−1)
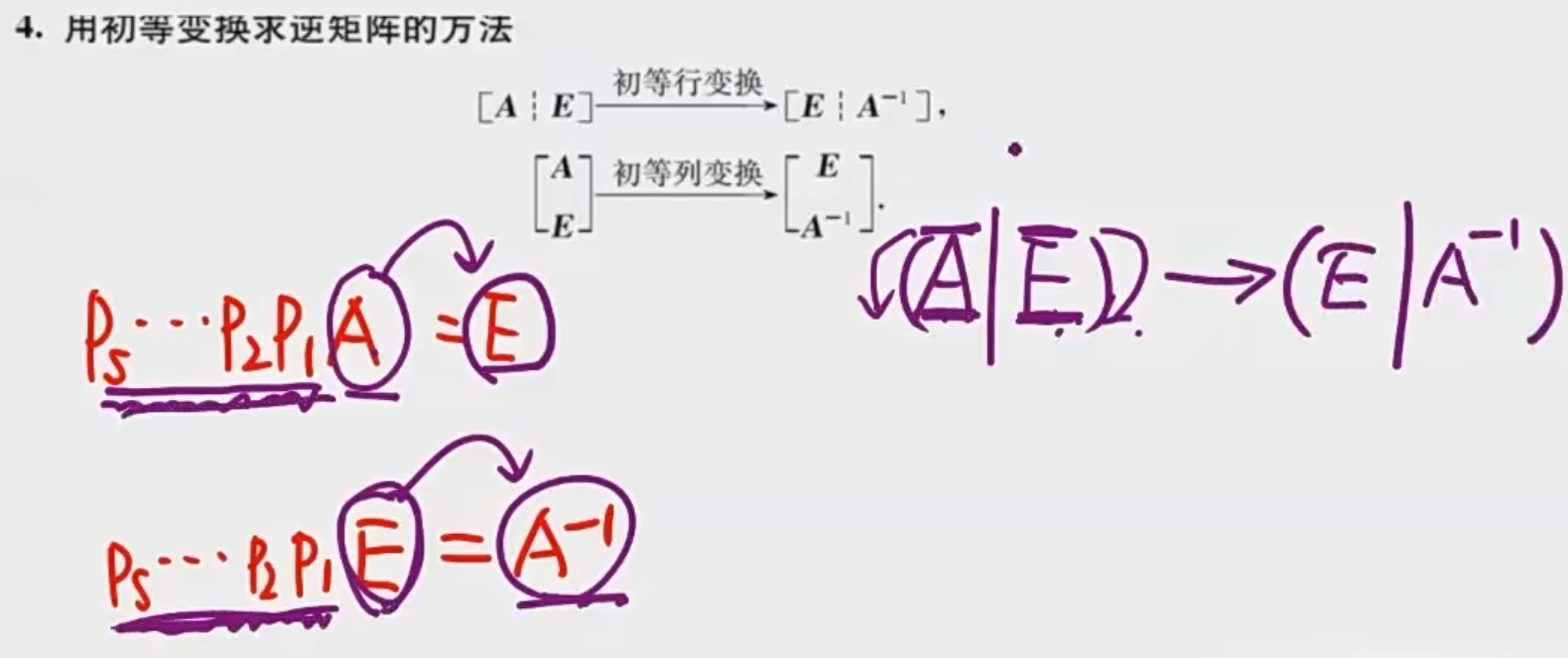
例题:2阶矩阵的逆矩阵 = 二阶矩阵的伴随矩阵 / 行列式
求二阶伴随矩阵A*:主对调,副变号

5.伴随矩阵 A*
(1)伴随矩阵的定义
若 A = ( a i j ) n × n = ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) A=(a_{ij})_{n×n}=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right) A=(aij)n×n= a11a21a31a12a22a32a13a23a33 ,则 A ∗ = ( A i j ) T = ( A 11 A 21 A 31 A 12 A 22 A 32 A 13 A 23 A 33 ) A^*=(A_{ij})^T=\left(\begin{array}{ccc} A_{11} & A_{21} & A_{31}\\ A_{12} & A_{22} & A_{32}\\ A_{13} & A_{23} & A_{33} \end{array}\right) A∗=(Aij)T= A11A12A13A21A22A23A31A32A33
(2)伴随矩阵性质 (伴随矩阵公式)
- A ⋅ A ∗ = A ∗ ⋅ A = ∣ A ∣ E ⇨ { A ∗ = ∣ A ∣ A − 1 A − 1 = A ∗ ∣ A ∣ A·A^* = A^*·A=|A|E\quad ⇨\quad \left\{ \begin{aligned} A^*=|A|A^{-1} \\ A^{-1}=\dfrac{A^*}{|A|} \end{aligned} \right. A⋅A∗=A∗⋅A=∣A∣E⇨⎩ ⎨ ⎧A∗=∣A∣A−1A−1=∣A∣A∗
若矩阵A可逆( A − 1 A^{-1} A−1存在),则其伴随矩阵和逆矩阵只差一个系数
推广为:🐕·🐕*=|🐕|E
推导: A ⋅ A ∗ = ( a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . a n 1 a n 2 . . . a n n ) ( A 11 A 21 . . . A n 1 A 12 A 22 . . . A n 2 . . . . . . . . . A 1 n A 2 n . . . A n n ) = ( ∣ A ∣ ∣ A ∣ . . . ∣ A ∣ ) = ∣ A ∣ E A·A^* =\left(\begin{array}{cccc} a_{11} &a_{12} &... &a_{1n} \\ a_{21}&a_{22} &... &a_{2n}\\ ...&... &&...\\ a_{n1}&a_{n2}&...&a_{nn} \end{array}\right)\left(\begin{array}{cccc} A_{11}&A_{21} &... &A_{n1} \\ A_{12}&A_{22} &... &A_{n2}\\ ...&... &&...\\ A_{1n}&A_{2n}&...&A_{nn} \end{array}\right)=\left(\begin{array}{cccc} |A| & & & \\ &|A| & &\\ & &...&\\ &&&|A| \end{array}\right)=|A|E A⋅A∗= a11a21...an1a12a22...an2.........a1na2n...ann A11A12...A1nA21A22...A2n.........An1An2...Ann = ∣A∣∣A∣...∣A∣ =∣A∣E
2. ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*| = |A|^{n-1} ∣A∗∣=∣A∣n−1
( A ∗ ) ∗ = ∣ A ∣ n − 2 ⋅ A (A^*)^*=|A|^{n-2}·A (A∗)∗=∣A∣n−2⋅A

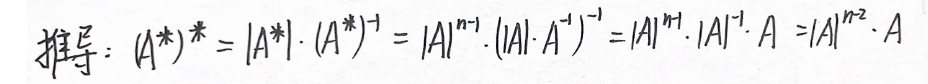
3. r ( A ∗ ) = { n , r ( A ) = n 1 , r ( A ) = n − 1 0 , r ( A ) < n − 1 r(A^*)= \left\{ \begin{aligned} n,\quad & r(A)=n \\ 1,\quad &r(A)=n-1 \\ 0,\quad &r(A)<n-1 \end{aligned} \right. r(A∗)=⎩ ⎨ ⎧n,1,0,r(A)=nr(A)=n−1r(A)<n−1
4. ( k A ∗ ) n = k n − 1 A ∗ (kA^*)^n=k^{n-1}A^* (kA∗)n=kn−1A∗
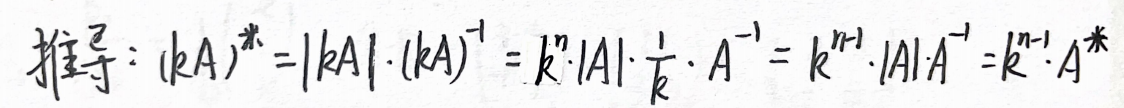
(3)求伴随矩阵
1.2阶伴随矩阵:
主对调,副变号
A = ( a b c d ) A=\left(\begin{array}{cc} a & b \\ c & d \end{array}\right) A=(acbd),则 A ∗ = ( d − b − c a ) A^*=\left(\begin{array}{cc} d & -b \\ -c & a \end{array}\right) A∗=(d−c−ba)
2.3阶伴随矩阵
3.n阶伴随矩阵
例题1:05年12.

分析:

答案:C
例题2:09年6.

答案:
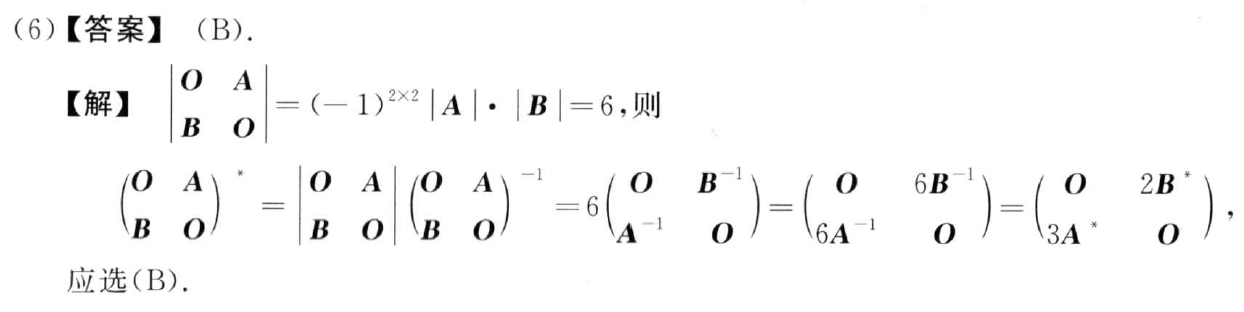
例题3:11年6. r(A*)的性质

分析:

答案:D
例题4:13年13.

分析:

答案:-1
6.初等变换 与 初等矩阵
(1)三种初等变换
以下三种变换,称为矩阵的初等变换:
1.倍乘:用非零常数k乘矩阵的某一行(列)
2.互换:互换矩阵中某两行(列)的位置
3.倍加:将矩阵的某一行(列)的k倍加到另一行(列)
①对行进行初等变换,称为初等行变换;对列进行初等变换,称为初等列变换
②初等行变换,不会改变列向量的关系
(2)初等变换性质
初等变换不改变矩阵的秩,可能改变特征值、迹、行列式的值。
相似变换和正交变换,不改变矩阵的特征值。
(3)初等矩阵
初等矩阵:由单位矩阵经过一次初等变换得到的矩阵
1.倍乘初等矩阵 E i ( k ) E_i(k) Ei(k):第 i i i行(或第2列)乘 k k k倍
2.互换初等矩阵 E i j E_{ij} Eij:第 i , j i,j i,j行(或第 i , j i,j i,j列)互换
3.倍加初等矩阵 E i j ( k ) E_{ij}(k) Eij(k):第 j j j行的 k k k倍加到第 i i i行 (或第 i i i列的k倍加到第 j j j列)


(4)初等矩阵的性质
| 初等矩阵\性质 | 转置 | 求逆 |
|---|---|---|
| ①互换初等矩阵 E i j E_{ij} Eij | E i j T = E i j {E_{ij}}^T= E_{ij} EijT=Eij,不变 | E i j − 1 = E i j {E_{ij}}^{-1}= E_{ij} Eij−1=Eij,不变 |
| ②倍乘初等矩阵 E i ( k ) E_i(k) Ei(k) | E i T ( k ) = E i ( k ) {E_i}^T(k)=E_i(k) EiT(k)=Ei(k),不变 | E i − 1 ( k ) = E i ( 1 k ) {E_i}^{-1}(k)=E_i(\dfrac{1}{k}) Ei−1(k)=Ei(k1) |
| ③倍加初等矩阵 E i j ( k ) E_{ij}(k) Eij(k) | E i j T ( k ) = E j i T ( k ) {E_{ij}}^T(k)={E_{ji}}^T(k) EijT(k)=EjiT(k),ij互换 | E i j − 1 ( k ) = E i j ( − k ) {E_{ij}}^{-1}(k)={E_{ij}}(-k) Eij−1(k)=Eij(−k) |

(5)左行右列定理:左乘行变换,右乘列变换
可逆矩阵P、Q, P A Q = B PAQ=B PAQ=B,则P为一系列行变换,Q为一系列列变换。
例题1:880 二次型 基础选择4 互换初等矩阵:求逆和转置均不变

分析:
互换初等矩阵 E i j E_{ij} Eij:
① E i j T = E i j {E_{ij}}^T= E_{ij} EijT=Eij,不变
② E i j − 1 = E i j {E_{ij}}^{-1}= E_{ij} Eij−1=Eij,不变
答案:A
例题2:23李林四(四)5. 左行右列定理


分析:
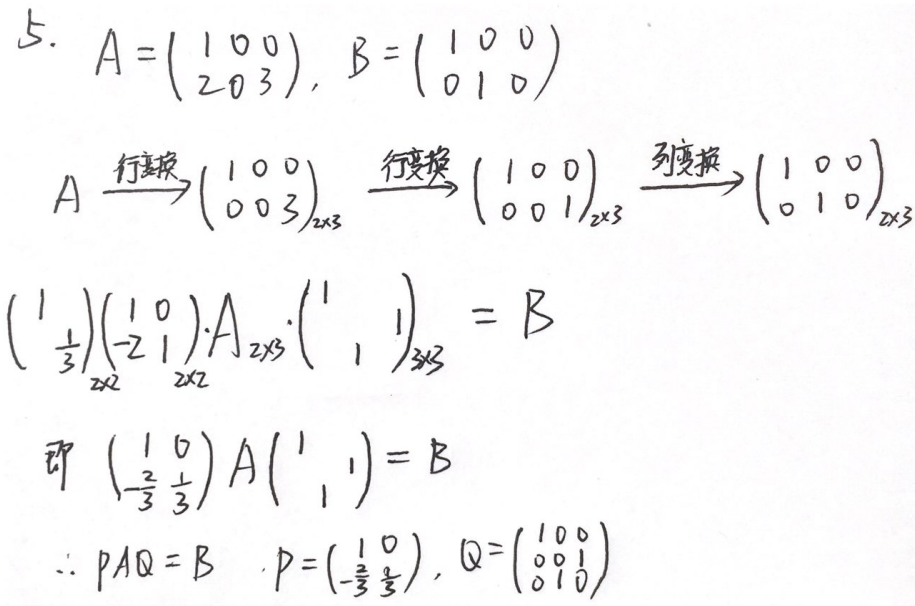
答案:D
例题2:880 向量 综合解答1(Ⅱ) 左行右列定理

例题3:14年13.
7.矩阵的秩
(1)矩阵的秩的定义
r(A)=k:
①最高阶非零子式的阶数为k
②至少存在一个k阶子式不为0,所有高于k阶的子式全为0
③矩阵秩的本质:组成该矩阵的线性无关的向量的个数,有且仅有k个
推论:若A有k阶子式 ≠ 0 ≠0 =0,则 r ( A ) ≥ k r(A)≥k r(A)≥k
k阶子式:A中任取k行k列,交叉点的元素按照原来的位置排列的k阶行列式,称为k阶子式。
(2)秩的性质
1. r ( A ) r(A) r(A) = r ( A T ) = r ( A A T ) = =r(A^T)=r(AA^T)= =r(AT)=r(AAT)= r ( A T A ) r(A^TA) r(ATA) 【2012年21(2)】
2. r ( A , B ) = r ( A , B ) T = r ( A T B T ) r(A,B)=r(A,B)^T=r\dbinom{A^T}{B^T} r(A,B)=r(A,B)T=r(BTAT) 【2018年6】
3.右乘列变换: r ( A ) = r ( A , A B ) r(A)=r(A,AB) r(A)=r(A,AB) 【2018年6】
左乘行变换: r ( A ) = r ( A B A ) r(A)=r\dbinom{A}{BA} r(A)=r(BAA)
4.若B可逆 /满秩为n,则 r ( A ) = r ( A B ) = r ( B A ) r(A)=r(AB)=r(BA) r(A)=r(AB)=r(BA)
5. r ( A B ) ≤ min { r ( A ) , r ( B ) } r(AB)≤\min\{ r(A),r(B)\} r(AB)≤min{r(A),r(B)}
6. max { r ( A ) , r ( B ) } ≤ r ( A , B ) ≤ r ( A ) + r ( B ) \max\{r(A),r(B)\}≤r(A,B)≤r(A)+r(B) max{r(A),r(B)}≤r(A,B)≤r(A)+r(B) 【2018年6】
联立3、4: r ( A B ) ≤ r ( A ) ≤ r ( A , B ) r(AB)≤r(A)≤r(A,B) r(AB)≤r(A)≤r(A,B)
7. r ( A + B ) ≤ r ( A ) + r ( B ) r(A+B)≤r(A)+r(B) r(A+B)≤r(A)+r(B) 【2013年21(2)】
8.若 A m × n B n × l = O A_{m×n}B_{n×l}=O Am×nBn×l=O,则 r ( A ) + r ( B ) ≤ n r(A)+r(B)≤n r(A)+r(B)≤n
9.若A为m×n矩阵,矩阵的秩≤行秩,≤列秩。即 r ( A m × n ) ≤ min { m , n } r(A_{m×n})≤\min\{m,n\} r(Am×n)≤min{m,n}
10.分块矩阵的秩:
① r ( A O O B ) = r ( A ) + r ( B ) r\left(\begin{array}{cc} A & O \\ O & B \end{array}\right)=r(A)+r(B) r(AOOB)=r(A)+r(B) 【23年5.】
② r ( A ) + r ( B ) ≤ r ( A O C B ) ≤ r ( A ) + r ( B ) + r ( C ) r(A)+r(B)≤r\left(\begin{array}{cc} A & O \\ C & B \end{array}\right)≤r(A)+r(B)+r(C) r(A)+r(B)≤r(ACOB)≤r(A)+r(B)+r(C)
11.若 α , β α,β α,β为非零列向量,则 r ( α β T ) = r ( β α T ) = 1 r(αβ^T)=r(βα^T)=1 r(αβT)=r(βαT)=1
12.矩阵方程 A X = B AX=B AX=B有解的充分必要条件是 r ( A ) = r ( A , B ) r(A)=r(A,B) r(A)=r(A,B)
13.对于 n ( n ≥ 2 ) n(n≥2) n(n≥2)阶矩阵 A A A,其伴随矩阵 A ∗ A^* A∗的秩为:
r ( A ∗ ) = { n , r ( A ) = n 1 , r ( A ) = n − 1 0 , r ( A ) < n − 1 r(A^*)= \left\{ \begin{aligned} n,\quad & r(A)=n \\ 1,\quad &r(A)=n-1 \\ 0,\quad &r(A)<n-1 \end{aligned} \right. r(A∗)=⎩ ⎨ ⎧n,1,0,r(A)=nr(A)=n−1r(A)<n−1
例题1:18年6.

分析:
A:右乘列变换: r ( A ) = r ( A , A B ) r(A)=r(A,AB) r(A)=r(A,AB)。A✔
B:左乘行变换: r ( A ) = r ( A B A ) r(A)=r\dbinom{A}{BA} r(A)=r(BAA)。B❌
C: max { r ( A ) , r ( B ) } ≤ r ( A , B ) ≤ r ( A ) + r ( B ) \max\{r(A),r(B)\}≤r(A,B)≤r(A)+r(B) max{r(A),r(B)}≤r(A,B)≤r(A)+r(B) 。C❌
D: r ( A , B ) = r ( A , B ) T = r ( A T B T ) r(A,B)=r(A,B)^T=r\dbinom{A^T}{B^T} r(A,B)=r(A,B)T=r(BTAT),D❌
答案:A
例题2:24李林六(一)7. (仿23年5.) 矩阵的初等行变换、初等列变换


分析:
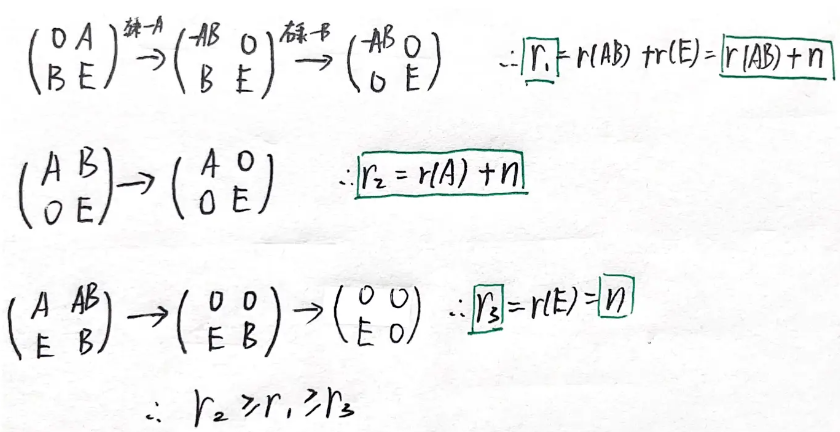
答案:A
例题3:23年5. 矩阵的初等行变换、初等列变换

分析:E为n阶单位矩阵,r(E)=n
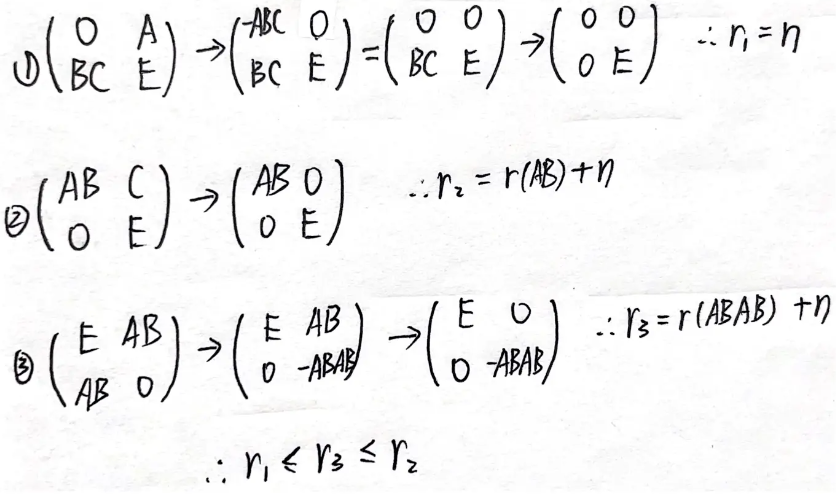
答案:B
例题4:24李林六(六)15.

答案:3
8.等价矩阵、等价标准型
1.等价矩阵:
①如果矩阵A经初等变换得矩阵B,则称矩阵A与矩阵B等价
②同型下,r(A)=r(B)
2.等价标准型:
满秩矩阵可经初等变换为单位阵,不满秩则只能化为 ( E r O O O ) \left(\begin{array}{cc} E_r & O \\ O & O \end{array}\right) (ErOOO)形式

这篇关于线性代数(基础篇):Ch1.行列式 Ch2.矩阵的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




