本文主要是介绍重构大学数学基础_week05_雅各比矩阵与雅各比行列式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
这周来讲一下雅各比矩阵和雅各比行列式。
多元函数的局部线性属性
首先我们来回顾一下向量函数，就是我们输入一个向量，输出也是一个向量，我们假设现在有一个向量函数
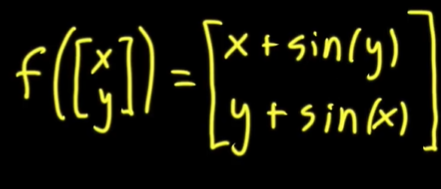
这个函数意思就是在说，我们在原来的平面上有一个向量(x,y),经过这个函数的变换后，他变成了向量(x+sin(y),y+sin(x))，很明显，这个变换是非线性的，原来的平面会扭曲成下面这个样子
但是这个函数变换有一个比较简单的性质，一个我们在整个微积分的学习中都能见到的性质，就是局部线性。
这意味着我们回到初始的XY平面，然后在某一个点放大很多倍再进行刚刚的非线性变换，
你会发现，这个点的局部变换非常接近线性
现在我们再回到没有变换之前的XY平面，然后考虑向右走一小步，就是沿着x方向走一小步记作
，而这一小步，在线性变换后的空间也变成了输出空间的一小步
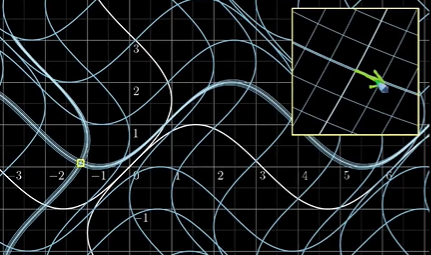
现在这个一小步不是单纯的x方向了而是具有了一定的y分量。
我们改写一下之前的函数，写成分量的形式，这样更加直观。
我们看到，我们一开始在x方向移动的一小步，其实产生了输出空间中两次微小的移动。我们对变换后的一小步进行分解为x方向和y方向，那么x方向的就是f1中改变的量，y方向的就是f2中改变的量，那么这两个分量就可以表示为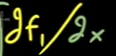
和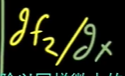
同理，我们在y 方向上移动的一小步分解后可以表示为
和
我们把它组合起来，这是一个2*2矩阵，这就是雅各比矩阵，雅各比矩阵就是归结于局部线性的思想，它从根本上就代表了，当你放大一个特定点的附近时变换的样子。
我们都知道，矩阵代表着一种线性变换，雅各比矩阵描述了函数在点(x,y) 附近如何改变空间的方向和大小。每一列向量代表了函数在该点沿着坐标轴方向的变化率，也就是函数图像在该点的“方向导数向量”。因此，雅各比矩阵揭示了函数在局部区域内的扭曲和拉伸效应，相当于一个线性变换，可以理解为从原点邻域到像点邻域的局部映射。
下面我们来看一下雅各比行列式。
首先我先简单说一下行列式的作用，我们一般认为行列式从衡量了矩阵的线性变换对空间的拉伸或者压缩的程度，行列式为0说明线性变换过程中产生了降维，行列式为负说明线性变换过程中基的方向发生了改变。
现在我们回到雅各比行列式中，我举个例子
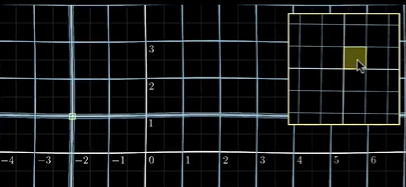
现在有一个黄色的矩形。我们对这个平面进行刚刚的线性变换，
那么这个矩阵的行列式就会告诉我们这个微小面积拉伸的比例
当然，描述这个放大区域变换的矩阵就是雅各比矩阵
举个例子：
（-2，1），在函数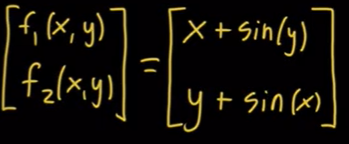
下，他的雅各比矩阵是
计算它的雅各比行列式，得到
说明拉伸了1.227倍。
总结：
1.雅各比矩阵揭示了一个多元函数在某点周围局部如何沿着各个坐标轴方向线性变化。
2.雅各比行列式揭示多元函数在某点的局部体积变形系数，即输入空间微小区域经过函数变换后在输出空间的体积相对变化。
3.雅各比矩阵是连接函数微分属性与其整体动态行为的桥梁。
4.雅各比行列式是优化和求解问题中判别系统稳定性与唯一性的重要指标。
雅各比矩阵及其行列式的应用：
1.计算机视觉：雅各比矩阵描述了图像在空间变换下的局部线性近似，如缩放、旋转和剪切等，使得图像能够被平滑地变形或校正。
2.敏感性分析：雅各比矩阵，可以评估模型输出对于输入变量的敏感度，即了解输入的小变动如何影响输出。这对于模型稳定性和鲁棒性分析非常重要。
3.梯度计算： 这一过程是反向传播算法的核心。虽然实际计算中通常处理的是梯度向量（雅可比矩阵的一行或一列），但理解雅可比矩阵有助于深入掌握梯度计算的本质。
这篇关于重构大学数学基础_week05_雅各比矩阵与雅各比行列式的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
