本文主要是介绍基于协方差信息的Massive MIMO信道估计算法性能研究,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 引言
随着移动互联网不断发展,人们对通信的速率和可靠性的要求越来越高[1]。目前第四代移动通信系统已经逐渐商用,研究人员开始着手研究下一代移动通信系统相关技术[2][3]。在下一代移动通信系统中要求下行速率达到10Gbps,这就要求我们使用更先进的技术和更宽的系统带宽。MIMO技术由于可以在不增加系统带宽和功率的前提下,成倍的提升系统容量和可靠性,已经广泛应用于各种无线通信系统中,但仅采用传统的MIMO技术很难实现10Gbps的速率需求,于是Bell实验室于2010年提出了Massive MIMO[4]的概念。Massive MIMO技术在基站侧设置大量天线,同时服务多个用户,其基站侧天线数远大于用户总的天线数,可以极大的提升系统的容量和可靠性[5][6],被认为是下一代移动通信系统可能的关键技术之一。
然而由于采用大规模的天线阵列,Massive MIMO的信道估计问题较MIMO系统更为突出,尤其是在多小区环境下,导频污染[4][5] [6]被认为是制约Massive MIMO性能的关键因素。因此,研究人员针对Massive MIMO的信道估计问题展开了大量的研究,根据Massive MIMO系统拥有大量多余的空间自由度的特点,提出了一系列对抗导频污染的信道估计算法,其中包括盲信道估计[7],基于子空间投影的信道估计[8],基于信道统计信息的信道估计[9][10]。其中基于信道协方差矩阵的信道估计算法[10]的实现相对简单,是本文主要讨论的对象。该算法要求基站拥有精确的本小区用户信道的协方差矩阵和相邻小区干扰用户信道的协方差矩阵,这在实际环境中往往无法得到,本文主要分析带误差的信道协方差矩阵对信道估计算法性能的影响,并提出一种信道的协方差矩阵的训练方法。
本文的结构如下:第2节,给出Massive MIMO的系统模型、信道建模方法以及线性预编码;第3节,给出了基于协方差信息的Massive MIMO信道估计算法以及信道的协方差矩阵的训练方法;第4节,在基站估计的信道协方差矩阵拥有不同大小误差的情况下,对信道估计算法的性能进行仿真,并对仿真结果进行分析;第5节,结论。
2. 系统模型
本文主要考虑在Massive MIMO系统上行链路中,在非视距、瑞利衰落环境下研究信道估计算法的性能。假定基站侧天线响应相关,用户侧天线响应不相干,且信道为平坦衰落,其系统模型如图1所示。
2.1 Massive MIMO系统模型
本文考虑系统中有L个时间同步的小区,即所有用户在同一时刻发送导频序列,并假定导频序列的长度为τ,且小区内的用户导频相互正交,而L个小区共用一组导频序列,则此时进行信道估计时就会受到来自其余L-1小区的导频干扰。同时在基站侧设置M根天线,为了简化分析假设每个小区内只有一个用户,在用户发送导频阶段,第j个小区的基站接收到的信号可以表示为:
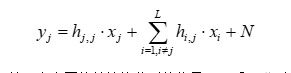
(1)
式中yj∈CM×τ表示第j个小区的基站接收到的信号,hi,j∈CM×1表示位于第i个小区的用户到的第j个小区基站侧M根天线的信道传输矩阵,xi∈C1×τ表示第i个小区的用户发送的信号,N∈CM×τ表示M根天线上的均值为零,方差为σn2的加性高斯白噪声,其中hj,j·xj表示目标小区用户的导频信号,∑Li=1,i≠j(hi,j·xj)表示来自其余L-1个小区用户的干扰。

图1 多小区的Massive MIMO的系统模型
2.2 Massive MIMO的信道模型
当在非视距情况下,不同用户的信号往往经过不同的路径,以不同的角度到达基站,如图2所示。因此假设基站侧的M根天线响应相关,而用户侧的响应相互独立,此时对Massive MIMO的信道传输矩阵h可以表示
![]()
(3)
式中Giid∈CM×1是复高斯分布的随机变量;RT∈CM×M是基站侧天线响应的相关矩阵,即信道的协方差矩阵,可以根据用户信号的到达角(AOA)功率谱P(θ)得到,当基站侧天线为线性天线阵列时,信道的协方差矩阵RT可以表示为:
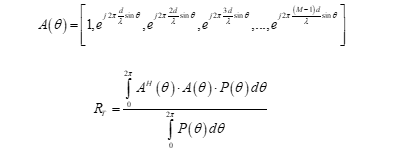
(4)
(5)
式中A(θ)表示当信号的到达角(AOA)为θ时,基站侧天线阵列的导向矢量。其中d表示基站侧天线间距,λ表示信号的波长。本文中考虑采用为高斯分布或者仅在某角度范围内有值、且为均匀分布的到达角(AOA)功率谱函数P(θ)来生成信道的协方差矩阵,分析不同分布情况下算法性能。
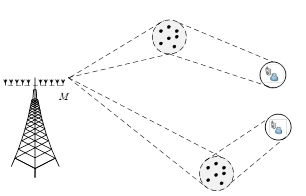
图2 Massive MIMO的系统的信道模型
3. 信道估计算法
为了简化分析,本文中主要考虑某特定小区估计的信道受其他小L-1个小区的影响情况,由于L个小区的用户使用长度为τ、且相同的导频序列,因此当第j个小区的基站采用LS算法得到的受导频污染影响的信道可以表示为

式中表示采用LS算法估计得到的信道,而即来自其他L-1个小区的导频污染。从式中可以看出,若在多小区的Massive MIMO系统中直接采用LS算法来进行信道估计,将会来自其他小区的干扰直接泄漏到估计的信道中,直接降低了Massive MIMO系统预编码和检测方法的有效性,严重制约了Massive MIMO性能的提升。
Massive MIMO系统的基站侧天线数远大于用户总的天线数,其拥有大量多余的空间自由度,如何利用系统多余的空间自由度为信道估计服务,是目前消除Massive MIMO信道估计中的导频污染影响的主要思想。
3.1基于协方差信息的Massive MIMO信道估计算法[10]
3.2信道的协方差矩阵的训练方法
基于协方差信息的Massive MIMO信道估计算法要求基站拥有所有用户的精确的信道协方差矩阵,由于信道协方差信息是慢时变的,这获取小区内的用户的精确的信道协方差矩阵比较容易实现,但是要获取相邻小区的干扰用户的精确的信道协方差矩阵将会比较困难。同时由于信道协方差矩阵的时变特性,导致估计的信道协方差矩阵与真实的信道协方差矩阵总存在一定的偏差,这就要求我们设计一种可以让基站获取多个小区用户的精确信道协方差矩阵的训练方法。
本文主要考虑非视距的Massive MIMO信道,信道的瞬时响应呈现小尺度衰落,但是依据上面Massive MIMO信道建模公式可知,信道协方差矩阵由用户信号的到达角功率谱函数P(θ),即实际信道中的散射体分布情况直接决定,其在相当大的一个频段范围内都是平坦的。在实际系统往往将Massive MIMO技术与OFDM技术相结合,因此利用少量子载波估计得到的信道协方差矩阵适用于所有子载波。
因此,本文提出以若干个小区一组,组内不同小区的用户在不同的子载波上发送用于训练其信道协方差矩阵的导频信号,用于训练其信道协方差矩阵的子载波在组内小区之间不再复用,以消除小区间干扰,提高信道协方差矩阵的估计精度,利用这种方法可以有效解决用户信道的协方差矩阵的训练问题,保证信道估计算法的性能。
4. 性能仿真与分析
本文主要考虑当基站用于信道估计的干扰用户的信道协方差矩阵包含不同程度的误差情况下,对基于协方差信息的Massive MIMO信道估计算法性能进行仿真,其中系统参数设置如表1所示。
首先是当基站拥有精确的信道协方差矩阵时,对基站侧设置不同天线数情况下的算法性能进行仿真。假设目标用户功率与干扰用户功率的比值为5dB,仿真结果如图3所示。从图中可以看出,当基站拥有目标用户和所有干扰用户精确的信道协方差矩阵时,随着基站侧天线数的增加,该信道
表1 仿真参数设置
| 系统参数 | 信道参数 | ||
| 小区数 | 2 | AOA分布 | 高斯分布 |
| 小区内用户数 | 1 | AOA均值 | 50゜/80゜ |
| 基站侧天线 | 4-128根(线性阵列) | AOA扩展角 | 10゜ |
| 天线间距 | λ/2 | 小区内用户SNR | 20dB |
| 工作频率 | 2.6Ghz | ||
| 仿真次数 | 10000 |
估计算法的估计误差迅速下降,当天线数达到128根时,信道估计误差接近-20dB,可见当基站拥有目标用户和所有干扰用户的精确的信道协方差矩阵时,该信道估计算法可以有效抑制来自其他小区的导频污染,提升系统性能。

图3 基站拥有精确的信道协方差信息时,信道估计精度与基站侧天线数的关系
然后仿真了在基站用于信道估计的信道协方差矩阵与实际的信道协方差矩阵有一定偏差情况下,当基站估计的信道协方差矩阵的AOA均值与实际的存在10゜的偏差时,对基站侧设置不同天线数情况下的算法性能进行仿真,假设目标用户功率与干扰用户功率的比值为5dB,仿真结果如图4所示。从图中可以看出,当基站用于信道估计的干扰用户的信道协方差矩阵存在误差时,随着基站侧天线数的增加,该算法的信道估计误差出现明显振荡现象,当天线数达到128根时,估计误差约为-8dB比理想情况下的性能要差12dB左右,可见当信道协方差矩阵存在误差时,算法性能急剧下降,这说明该算法不适用于无法获取用户的实时的精确的信道协方差信息的信道情况。
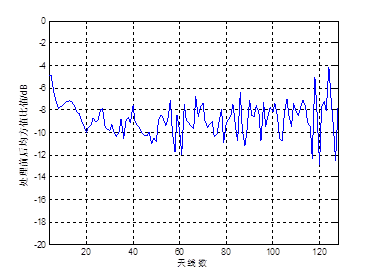
图4 基站拥有的信道协方差信息含噪声时,信道估计精度与基站侧天线数的关系
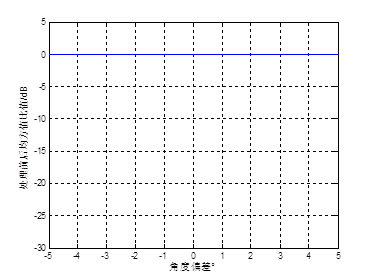
图5 算法处理前后的目标信号的均方值比值与干扰用户的信道协方差矩阵估计精度的关系
最后仿真了当基站用于信道估计的干扰用户的信道协方差矩阵包含不同程度的误差情况下,该算法对导频污染的抑制能力。仿真了当基站拥有目标用户的精确信道协方差矩阵,同时基站估计的干扰用户的信道协方差矩阵的AOA均值与实际AOA均值的偏差从-5゜到5゜时,基站侧天线数为128根,算法处理前后的目标信号、干扰信号和系统噪声的均方值比值的仿真结果如图5、6、7所示。从图中可以看出,干扰用户的信道协方差矩阵存在一定偏差时,不会对目标信号的提取和对高斯白噪声的抑制产生影响,l1保持在0dB左右,l3保持在-5dB左右。而当出现角度偏差时,该算法对干扰信号的抑制能力将会出现振荡现象,振荡的幅值达到15dB,l2最好可以达到-27.4dB左右,l2最差仅为-13dB,可见当基站估计的干扰用户的信道协方差矩阵与实际的信道协方差矩阵存在一定偏差时,该信道估计算法的性能将会大幅下降。
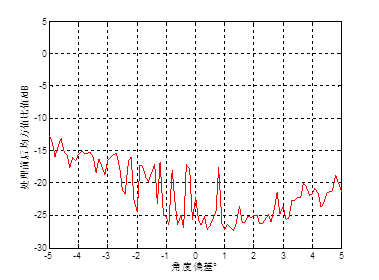
图6 算法处理前后的干扰信号的均方值比值与干扰用户的信道协方差矩阵估计精度的关系
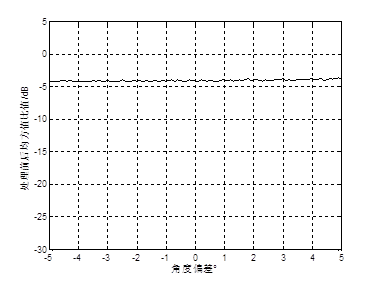
图7 算法处理前后的系统热噪声的均方值比值与干扰用户的信道协方差矩阵估计精度的关系
5. 结论
在Massive MIMO系统中,若用户信道位于不同向量子空间,则可以利用用户信道的协方差矩阵可以有效地提取目标用户的信道传输矩阵。但若用于信道估计的协方差信息与实际的信道传输矩阵存在一定的偏差时,该算法性能快速下降,说明该算法需要所有用户的精确的信道协方差信息。针对精确的信道协方差信息的获取问题,本文提出了一种信道的协方差信息的训练方法,使基站可以获取目标用户和所有干扰用户的精确且实时的信道协方差矩阵,这对该信道估计算法应用于实际的Massive MIMO系统的信道估计拥有非常重要的意义。
这篇关于基于协方差信息的Massive MIMO信道估计算法性能研究的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








