本文主要是介绍数学期望，方差，标准差，样本方差，协方差，相关系数概念扫盲，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
数学期望
在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。
再举个例子理解一下数学期望：
方差
概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。
标准差
标准差是方差算术平方根
样本方差
如是总体,标准差公式根bai号内除以n
如是样本,标准差公式根号内除以（n-1)
协方差
协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
从直观上来看，协方差表示的是两个变量总体误差的期望。
如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
如果X与Y是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足E[XY]=E[X]E[Y]。但是，反过来并不成立。即如果X与Y的协方差为0，二者并不一定是统计独立的。
协方差Cov(X,Y)的度量单位是X的协方差乘以Y的协方差。
协方差为0的两个随机变量称为是不相关的。
性质
若两个随机变量X和Y相互独立，则E[(X-E(X))(Y-E(Y))]=0，因而若上述数学期望不为零，则X和Y必不是相互独立的，亦即它们之间存在着一定的关系。
协方差与方差之间有如下关系：
D(X+Y)=D(X)+D(Y)+2Cov(X，Y)
D(X-Y)=D(X)+D(Y)-2Cov(X，Y)
协方差与期望值有如下关系：
Cov(X，Y)=E(XY)-E(X)E(Y)。
协方差的性质：
（1）Cov(X，Y)=Cov(Y，X)；
（2）Cov(aX，bY)=abCov(X，Y)，（a，b是常数）；
（3）Cov(X1+X2，Y)=Cov(X1，Y)+Cov(X2，Y)。
由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)。
相关系数
协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念：
定义
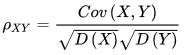
称为随机变量X和Y的(Pearson)相关系数。
若ρXY=0，则称X与Y不线性相关。
即ρXY=0的充分必要条件是Cov(X，Y)=0，亦即不相关和协方差为零是等价的。
定理
设ρXY是随机变量X和Y的相关系数，则有（1）∣ρXY∣≤1；
（2）∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）
相关系数的参考文章指路：相关系数
Tips: 期望与平均值的区别
期望和均值原来容易会弄混，但其实他们是完全不同的概念，那么分别来介绍均值和期望看看他们的不同点。
一、均值
均值，其实是针对实验观察到的特征样本而言的。比如我们实验结果得出了x1,x2,x3……xn这n个值，那么我们的均值计算是
比如我们进行掷骰子，掷了六次，点数分别为2，2，2，4，4，4，这六次的观察就是我们的样本，于是我们可以说均值为(2+2+2+4+4+4)/6=3。但是千万不能说期望是3，说概率是3就明显的弄混了均值和期望的概念，下面解释一下期望的概念。
二、期望
期望是针对于随机变量而言的一个量，可以理解是一种站在“上帝视角”的值。针对于他的样本空间而言的。
均值是一个统计量(对观察样本的统计)，期望是一种概率论概念，是一个数学特征。
首先给出定义公式
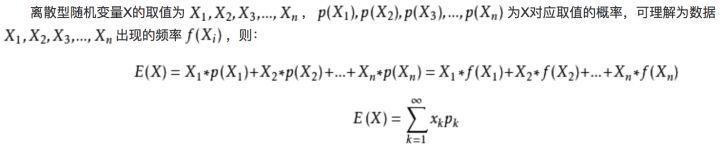那么上面那个掷骰子例子对应的期望求法如下：
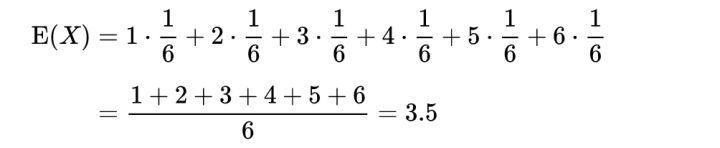可以看出期望是与概率值联系在一起的，如果说概率是频率随样本趋于无穷的极限 ，期望就是平均数随样本趋于无穷的极限，可以看出均值和期望的联系也是大数定理联系起来的。
三、例子
上面说到期望就是平均数随样本趋于无穷的极限，那么这句话是什么意思呢？
我们还是以上面的掷骰子为例子：
如果我们掷了无数次的骰子，然后将其中的点数进行相加，然后除以他们掷骰子的次数得到均值，这个有无数次样本得出的均值就趋向于期望。类似于下面这样：
四、总结
概率是频率随样本趋于无穷的极限
期望是平均数随样本趋于无穷的极限
这篇关于数学期望，方差，标准差，样本方差，协方差，相关系数概念扫盲的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
