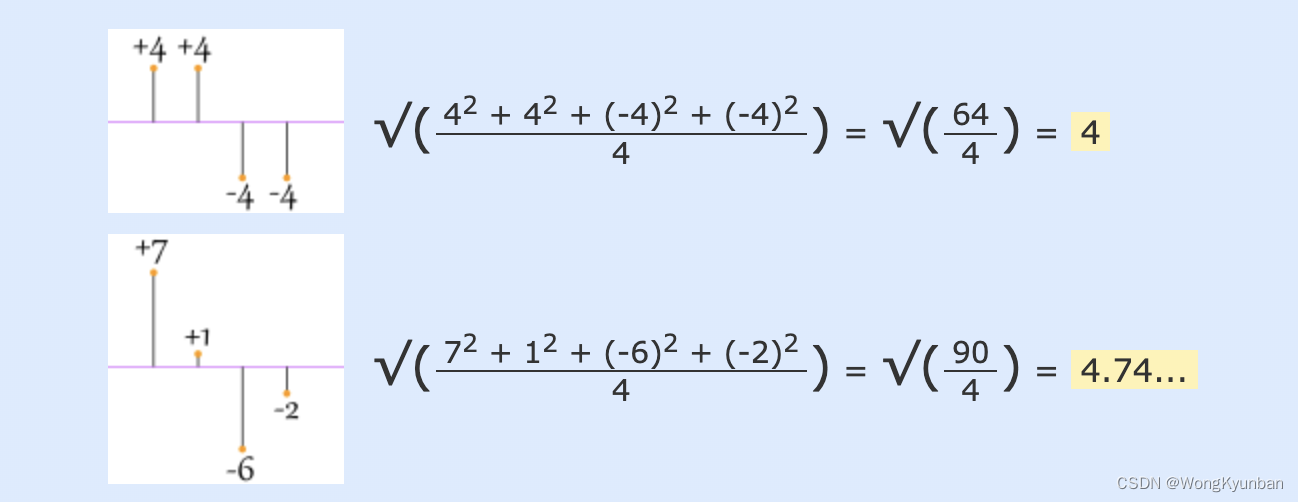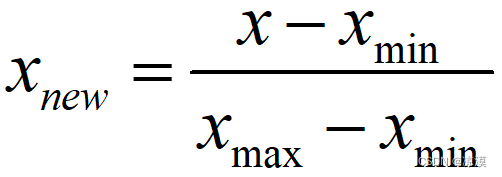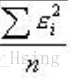方差专题
【深度学习 误差计算】10分钟了解下均方差和交叉熵损失函数
常见的误差计算函数有均方差、交叉熵、KL 散度、Hinge Loss 函数等,其中均方差函数和交叉熵函数在深度学习中比较常见,均方差主要用于回归问题,交叉熵主要用于分类问题。下面我们来深刻理解下这两个概念。 1、均方差MSE。 预测值与真实值之差的平方和,再除以样本量。 均方差广泛应用在回归问题中,在分类问题中也可以应用均方差误差。 2、交叉熵 再介绍交叉熵损失函数之前,我们首先来介绍信息
概率学 笔记一 - 概率 - 随机变量 - 期望 - 方差 - 标准差(也不知道会不会有二)
概率不用介绍,它的定义可以用一个公式写出: 事件发生的概率 = 事件可能发生的个数 结果的总数 事件发生的概率=\cfrac{事件可能发生的个数}{结果的总数} 事件发生的概率=结果的总数事件可能发生的个数 比如一副标准的 52 张的扑克牌,每张牌都是唯一的,所以,抽一张牌时,每张牌的概率都是 1/52。但是有人就会说了,A 点明明有四张,怎么会是 1/52 的概率。 这就需要精准的指出
方差(Variance) 偏差(bias) 过拟合 欠拟合
机器学习中方差(Variance)和偏差(bias)的区别?与过拟合欠拟合的关系? (1)bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。 低偏差和高方差(对应右上图)是使得模型复杂,增加了模型的参数,这样容易过拟合。 这种情况下,形象的讲,瞄的很准,但手不一定稳。 (2)varience描述的是样本上训练出来的模型
NumPy(五):数组统计【平均值:mean()、最大值:max()、最小值:min()、标准差:std()、方差:var()、中位数:median()】【axis=0:按列运算;axis=0:按列】
统计运算 np.max()np.min()np.median()np.mean()np.std()np.var()np.argmax(axis=) — 最大元素对应的下标np.argmin(axis=) — 最小元素对应的下标 NumPy提供了一个N维数组类型ndarray,它描述了 相同类型 的“items”的集合。(NumPy provides an N-dimensional array
平均值,标准差,方差,协方差,期望,均方误差
1. 写在前面 平均值,标准差,方差,协方差都属于统计数学;期望属于概率数学。 2. 统计数学 2.1 平均值,标准差,方差 统计学里最基本的概念就是样本的均值、方差、标准差。首先,我们给定一个含有n个样本的集合,下面给出这些概念的公式描述: 均值: 方差: 标准差: 均值描述的是样本集合的中间点,它告诉我们的信息是有限的。 方差(variance)是在概率论和统计方差衡量随机变
吴恩达机器学习课后作业-05偏差与方差
偏差与方差 题目欠拟合改进欠拟合影响偏差和方差因素训练集拟合情况训练集和测试集代价函数选择最优lamda 整体代码 训练集:训练模型 ·验证集︰模型选择,模型的最终优化 ·测试集:利用训练好的模型测试其泛化能力 #训练集x_train,y_train = data['X'],data[ 'y']#验证集x_val,y_val = data['Xval'],dat
机器学习和数据挖掘(8):偏见方差权衡
偏见方差权衡 偏见和方差 我们一直试图在近似和泛化之间找到一个平衡。 我们的目标是得到一个较小的 Eout E_{out},也希望在样例之外也表现得非常棒的 Eout E_{out}。复杂的假设集 H \mathcal H将有机会得到一个接近目标函数的结果。 VC维分析使用的是泛化边界来进行泛化。根据公式 Eout≤Ein+Ω E_{out}\leq E_{in}+\Omega,其中 Ei
回归分析系列18— 平衡偏差与方差
22 平衡偏差与方差 22.1 偏差-方差权衡简介 在模型构建中,我们通常面临偏差(bias)与方差(variance)之间的权衡。偏差是指模型的预测与真实值之间的系统性误差,而方差则是指模型在不同训练集上的波动性。 高偏差通常意味着模型过于简单,无法捕捉数据中的复杂模式(即欠拟合);高方差则意味着模型对训练数据过于敏感,导致在新数据上表现不佳(即过拟合)。 22.2 正则化与偏差-方差
方差:理解数据的离散程度
方差:理解数据的离散程度 文章目录 方差:理解数据的离散程度引言样本与总体的关系什么是方差?方差的数学公式有偏估计 vs. 无偏估计 方差的计算示例无偏估计的推导与重要性从有偏估计到无偏估计的推导Bessel校正的原因是否总是需要无偏估计? 方差的应用场景结论 引言 方差是统计学和数据分析中的重要概念,用于量化数据集中各个观测值与平均值之间的差异程度。理解方差有助
方差的原理以及应用场景
方差是统计学中一个重要的概念,用来衡量一组数据的离散程度或波动性。具体来说,方差描述了数据点与其均值之间的平均平方差。方差越大,说明数据点的波动性或不确定性越大;方差越小,说明数据点集中在均值附近,波动性较小。 方差的计算原理 给定一组数据 ( X_1, X_2, \dots, X_n ),其方差计算公式为: [ \text{方差} = \frac{1}{n} \sum_{i=1}^{n}
【数据分析】数据的离中趋势之二 - 方差和标准差、离散系数
四、方差和标准差 方差是数据组中各数据值与其算术平均数离差平方的算术平均数。方差的平方根就是标准差标准差的本质与平均差基本相同,平均差取绝对值的方法消除离差正负号后用算数平均的方法求平均离差。标准差用平方的方法消除离差的正负号后用离差平方求平均数再开根号。标准差的性质: 标准差度量了偏离平均数的大小标准差是一类平均偏差数列大多数项距离平均数少于1个标准差范围内,极少数项距离平均数 2个 或者 3
MATLAB算法实战应用案例精讲-【数模应用】三因素方差
目录 算法原理 SPSSAU 三因素方差案例 1、背景 2、理论 3、操作 4、SPSSAU输出结果 5、文字分析 6、剖析 疑难解惑 均方平方和类型? 事后多重比较的类型选择说明? 事后多重比较与‘单独进行事后多重比较’结果不一致? 简单效应是指什么? 边际估计均值EMMEANS是什么? 简单简单效应? 关于方差分析时的效应量? SPSSAU-案例 一、案例
证明 几何分布 的期望和方差
几何分布 几何分布(Geometric Distribution)描述了在进行一系列独立的伯努利试验时,第一次成功所需的试验次数。假设每次试验成功的概率为 ( p ),则几何分布的概率质量函数(PMF)为: P ( X = k ) = ( 1 − p ) k − 1 p , k = 1 , 2 , 3 , … P(X = k) = (1 - p)^{k-1} p, \quad k = 1,
PyTorch 入坑十:模型泛化误差与偏差(Bias)、方差(Variance)
问题 阅读正文之前尝试回答以下问题,如果能准确回答,这篇文章不适合你;如果不是,可参考下文。 为什么会有偏差和方差?偏差、方差、噪声是什么?泛化误差、偏差和方差的关系?用图形解释偏差和方差。偏差、方差窘境。偏差、方差与过拟合、欠拟合的关系?偏差、方差与模型复杂度的关系?偏差、方差与bagging、boosting的关系?偏差、方差和K折交叉验证的关系?如何解决偏差、方差问题? 本文主要参考知
吴恩达2022机器学习专项课程C2W3:2.25 理解方差和偏差(诊断方差偏差正则化偏差方案搭建性能学习曲线)
目录 引言名词替代影响模型偏差和方差的因素1.多项式阶数2.正则化参数 判断是否有高偏差或高方差1.方法一:建立性能基准水平2.方法二:建立学习曲线 解决线性回归高偏差或高方差解决神经网络的高偏差或高方差1.回顾机器学习问题2.神经网络高方差和高偏差3.神经网络正则化 神经网络如何正则化总结 引言 机器学习系统开发的典型流程是从一个想法开始,然后训练模型。初次训练的结果通常不理想
【Tools】什么是方差
我们都找到天使了 说好了 心事不能偷藏着 什么都 一起做 幸福得 没话说 把坏脾气变成了好沟通 我们都找到天使了 约好了 负责对方的快乐 阳光下 的山坡 你素描 的以后 怎么抄袭我脑袋 想的 🎵 薛凯琪《找到天使了》 方差是统计学中的一个重要概念,用于描述一组数据的离散程度或分散程度。具体来说,方差反映了数据中每个值与均值之间的差距的平方的平均
证明 泊松分布 的期望和方差
泊松分布 泊松分布(Poisson Distribution)是描述在固定时间间隔内某事件发生次数的概率分布,特别适用于稀有事件的统计。假设随机变量 ( X ) 表示在时间间隔 ( t ) 内某事件发生的次数,并且该事件在单位时间内发生的平均次数为 ( \lambda )。那么 ( X ) 服从参数为 ( \lambda ) 的泊松分布,记作 泊松分布的概率质量函数(PMF)为: P (
Python, Numpy求 list 数组均值,方差,标准差
代码如下: import numpy as np array = [1,3,5,7,9]# 求均值arr_mean = np.mean(array)# 求方差arr_var = np.var(array)# 求标准差arr_std = np.std(array,ddof=1)
数据预处理——调整方差、标准化、归一化(Matlab、python)
对数据的预处理: (a)、调整数据的方差; (b)、标准化:将数据标准化为具有零均值和单位方差;(均值方差归一化(Standardization)) (c)、最值归一化,也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 , 1]之间 (a)、调整数据的方差 均方差=标准差 方差的定义是:离平均值的平方距离的平均。 (b)、标准化 也称为均值归一化(me
方差的计算(总体方差与样本方差)
方差是数据集中的各个数据与其均值之间差值的平方的平均值。方差的计算公式如下: 对于总体数据(即所有数据): σ 2 = 1 N ∑ i = 1 N ( x i − μ ) 2 \sigma^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2 σ2=N1i=1∑N(xi−μ)2 其中: σ 2 是总体方差。 \sigma^2是总体方差。 σ2是总体
关于样本方差的分母是 ( n-1 ) 而不是 ( n )的原因
样本方差的分母是 ( n-1 ) 而不是 ( n ) 的原因与统计学中的“自由度”概念有关。使用 ( n-1 ) 作为分母可以使样本方差成为总体方差的无偏估计量。 自由度 在计算样本方差时,我们需要先计算样本均值 ( \bar{x} )。样本中的 ( n ) 个数据点中,实际上只有 ( n-1 ) 个数据点是自由变化的,因为最后一个数据点可以通过样本均值和前面的 ( n-1 ) 个数据点确定。
《python程序语言设计》2018版第5章第46题均值和标准方差-下部(本来想和大家说抱歉,但成功了)
接上回,5.46题如何的标准方差 本来想和大家说非常抱歉各位同学们。我没有找到通过一个循环完成两个结果的代码。 但我逐步往下的写,我终于成功了!! 这是我大前天在单位找到的公式里。x上面带一横是平均值。 我不能用函数的办法封装循环。所以我只能从循环里找办法。可是 我建立 了第一个循环 step_num = 0num_c = 0pow_c = 0while step_num <
方差、标准差、均方误差和均方根误差
最近在整机器学习的内容,这个概念稍微有点乱,百度一下,里清楚了,做个记录: 一、白话描述 1、方差的二次开方等于标准差 2、均方误差的二次开方等于均方根误差。 3、方差是每个样本减去总样本的平均值去计算的,而均方误差是每个样本减去该样本的真实值来计算的 所以,方差、标准差是数学上的概念,而均方误差是在机器学习中用的比较多的概念,计算loss的时候会用,实际上原理是类似的,但是具体计算上稍
从零开始学统计 03 | 均值,方差,标准差
一、均值 现在,假设已经拿到在实际的肝脏中大约 2400 亿个细胞的X基因表达值。 我们接下来,要计算总体均值与估计总体均值。 现在使用实际的2400亿个细胞计算均值,也就是总体均值(Population Mean) 从总体中抽样 5 个样本,计算估计均值(Estimated Mean): 统计学中,用符号x-bar () 来表示估计均值,也叫样本均值(Sample Mea