本文主要是介绍方差、标准差、均方误差和均方根误差,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近在整机器学习的内容,这个概念稍微有点乱,百度一下,里清楚了,做个记录:
一、白话描述
1、方差的二次开方等于标准差
2、均方误差的二次开方等于均方根误差。
3、方差是每个样本减去总样本的平均值去计算的,而均方误差是每个样本减去该样本的真实值来计算的
所以,方差、标准差是数学上的概念,而均方误差是在机器学习中用的比较多的概念,计算loss的时候会用,实际上原理是类似的,但是具体计算上稍微有些差别。这是我的理解(不一定正确),下面贴上一些具体的解释。
二、详细解释
一、百度百科上方差是这样定义的:
(variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是各个数据分别与其平均数之差的平方的和的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
看这么一段文字可能有些绕,那就先从公式入手,
对于一组随机变量或者统计数据,其期望值我们由E(X)表示,即随机变量或统计数据的均值,
然后对各个数据与均值的差的平方求和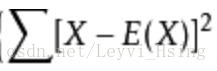
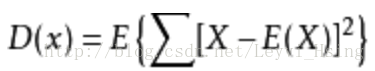
这个公式描述了随机变量或统计数据与均值的偏离程度。
二、方差与标准差之间的关系就比较简单了
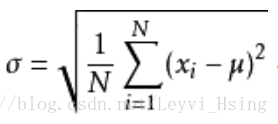
根号里的内容就是我们刚提到的
那么问题来了,既然有了方差来描述变量与均值的偏离程度,那又搞出来个标准差干什么呢?
发现没有,方差与我们要处理的数据的量纲是不一致的,虽然能很好的描述数据与均值的偏离程度,但是处理结果是不符合我们的直观思维的。
举个例子:一个班级里有60个学生,平均成绩是70分,标准差是9,方差是81,成绩服从正态分布,那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分,通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为0.6826,即约等于下图中的34.2%*2 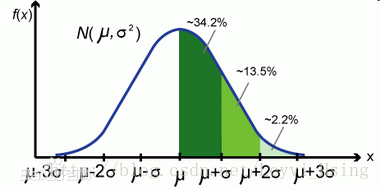
三、均方差、均方误差又是什么?
标准差(Standard Deviation) ,中文环境中又常称均方差,但不同于均方误差(mean squared error,均方误差是各数据偏离真实值的距离平方和的平均数,也即误差平方和的平均数,计算公式形式上接近方差,它的开方叫均方根误差,均方根误差才和标准差形式上接近),标准差是离均差平方和平均后的方根,用σ表示。标准差是方差的算术平方根。
从上面定义我们可以得到以下几点:
1、均方差就是标准差,标准差就是均方差
2、均方误差不同于均方误差
3、均方误差是各数据偏离真实值的距离平方和的平均数
举个例子:我们要测量房间里的温度,很遗憾我们的温度计精度不高,所以就需要测量5次,得到一组数据[x1,x2,x3,x4,x5],假设温度的真实值是x,数据与真实值的误差e=x-xi
那么均方误差MSE=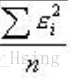
总的来说,均方差是数据序列与均值的关系,而均方误差是数据序列与真实值之间的关系,所以我们只需要搞清楚真实值和均值之间的关系就行了。
这篇关于方差、标准差、均方误差和均方根误差的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








