均方专题

平均值，标准差，方差，协方差，期望，均方误差

1. 写在前面平均值，标准差，方差，协方差都属于统计数学；期望属于概率数学。 2. 统计数学 2.1 平均值，标准差，方差统计学里最基本的概念就是样本的均值、方差、标准差。首先，我们给定一个含有n个样本的集合，下面给出这些概念的公式描述：均值：方差：标准差：均值描述的是样本集合的中间点，它告诉我们的信息是有限的。方差（variance)是在概率论和统计方差衡量随机变

数学基础 -- 均方误差（Mean Squared Error, MSE）与交叉熵（Cross-Entropy）的数学原理

均方误差（Mean Squared Error, MSE）与交叉熵（Cross-Entropy）的数学原理 1. 均方误差（Mean Squared Error, MSE）均方误差主要用于回归问题，度量预测值与实际值之间的平均平方差。其数学公式为： MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i

PyTorch nn.MSELoss() 均方误差损失函数详解和要点提醒

文章目录 nn.MSELoss() 均方误差损失函数参数数学公式元素版本要点附录参考链接 nn.MSELoss() 均方误差损失函数 torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean') Creates a criterion that measures the mean squared err

方差、标准差、均方误差和均方根误差

最近在整机器学习的内容，这个概念稍微有点乱，百度一下，里清楚了，做个记录：一、白话描述 1、方差的二次开方等于标准差 2、均方误差的二次开方等于均方根误差。 3、方差是每个样本减去总样本的平均值去计算的，而均方误差是每个样本减去该样本的真实值来计算的所以，方差、标准差是数学上的概念，而均方误差是在机器学习中用的比较多的概念，计算loss的时候会用，实际上原理是类似的，但是具体计算上稍

残差平方和（RSS）、均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)

残差平方和（RSS）等同于SSE（误差项平方和）实际值与预测值之间差的平方之和。 MSE: Mean Squared Error 均方误差是RSS的期望值（或均值）; MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。 RMSE 均方根误差:均方根误差是均方误差的算术平方根 MAE :Mean Absolute Error 平均绝对误差是绝对

sklearn【MSE】均方误差，原理及学习代码！

一、MSE 介绍均方误差（Mean Squared Error，MSE）是回归问题中常用的一个评估指标，它通过计算预测值与实际值之间差异的平方的平均值来评估模型的精度。在Python的机器学习库sklearn中，我们可以使用内置的mean_squared_error函数来计算MSE。具体来说，MSE的计算步骤如下：收集数据：首先，我们需要一组包含实际目标值（真实值）和模型预测值的数

【推导结果】如何得到回归均方误差估计系数的标准误

对线性回归模型系数标准差标准误的理解 1.生成数据 yxe3.610.633.42-1.387.631.017.44-1.0111.651.3811.46-0.63 2.回归 y = β 0 + β 1 x + ϵ y = \beta_{0}+\beta_{1}x+\epsilon y=β0+β1x+ϵ y i = β 0 + β 1 x i + e i y_{i}=\bet

为什么交叉熵损失可以提高具有sigmoid和softmax输出的模型的性能，而使用均方误差损失则会存在很多问题

最小均方误差算法(LMSE) - 知乎

深度学习入门（python）考试速成均方误差

均方误差表示神经网络的输出，表示监督数据，表示数据的维度。这里神经网络的输出y是softmax函数的输出数组元素的索引从第一个开始依次对应数组“0”，“1”，“2”，...... 由于softmax函数的输出可理解为概率由此上例表示“0”的概率为0.1，“1”的概率为0.05，“2”的概率为0.6等 t是监督数据，将正确解标签设为1，其他设为0。这里标签“2”的数值

深度学习入门（python）考试速成均方误差

均方误差表示神经网络的输出，表示监督数据，表示数据的维度。这里神经网络的输出y是softmax函数的输出数组元素的索引从第一个开始依次对应数组“0”，“1”，“2”，...... 由于softmax函数的输出可理解为概率由此上例表示“0”的概率为0.1，“1”的概率为0.05，“2”的概率为0.6等 t是监督数据，将正确解标签设为1，其他设为0。这里标签“2”的数值

机器学习从矩阵和概率的角度解释最小均方误差函数

最小均方误差函数之前的讲义里，我们提到了最小均方误差函数，给出一组有 m m 个样本的训练集，我们希望找到合适的参数 θ\boldsymbol{\theta}，使得预测值 hθ(x) h_\theta(x) 与目标值尽可能接近。为了估计参数 θ \boldsymbol{\theta}，我们定义如下的 cost function: J(θ)=12∑i=1m(hθ(xi)−y

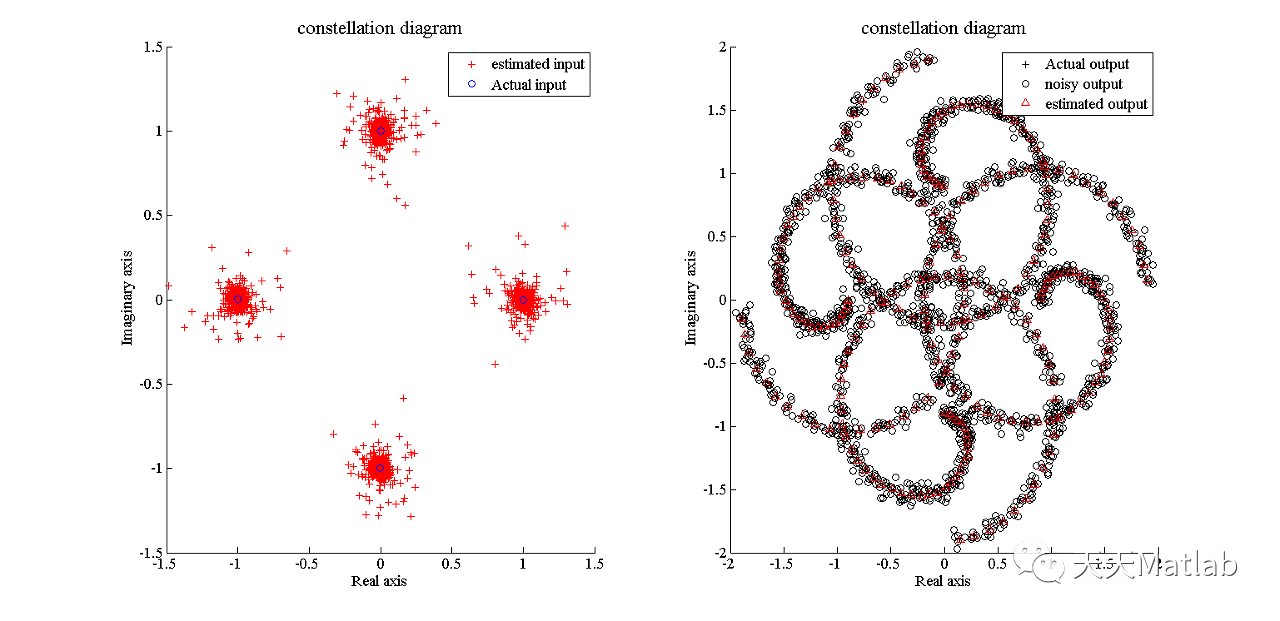
基于最小均方 (LMS) 算法实现线性信道估计附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。 🍎个人主页：Matlab科研工作室 🍊个人信条：格物致知。更多Matlab仿真内容点击👇 智能优化算法神经网络预测雷达通信无线传感器信号处理图像处理路径规划元胞自动机无人机电力系