证明 泊松分布 的期望和方差

本文主要是介绍证明 泊松分布 的期望和方差，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

泊松分布

泊松分布（Poisson Distribution）是描述在固定时间间隔内某事件发生次数的概率分布，特别适用于稀有事件的统计。假设随机变量 ( X ) 表示在时间间隔 ( t ) 内某事件发生的次数，并且该事件在单位时间内发生的平均次数为 ( \lambda )。那么 ( X ) 服从参数为 ( \lambda ) 的泊松分布，记作

泊松分布的概率质量函数（PMF）为：

$$P(X=k)=\frac{{\lambda }^k{e}^{-\lambda }}{k!},k=0,1,2,\dots$$

期望值

期望值（Expectation）表示随机变量的平均值。对于泊松分布 ( X )，其期望值 ( \mathbb{E}(X) ) 定义为：

$$\mathbb{E}(X)=\sum _{k=0}^{\infty }k\cdot P(X=k)$$

代入泊松分布的概率质量函数：

$$\mathbb{E}(X)=\sum _{k=0}^{\infty }k\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}$$

我们将求和从 ( k = 1 ) 开始，因为当 ( k = 0 ) 时，项为零：

$$\mathbb{E}(X)=\sum _{k=1}^{\infty }k\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}$$

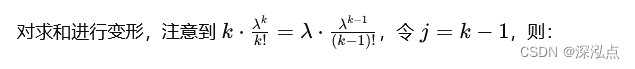
$$\mathbb{E}(X)=\lambda \sum _{j=0}^{\infty }\frac{{\lambda }^j{e}^{-\lambda }}{j!}$$

由泊松分布的性质，指数部分和概率质量函数的和为 1：

$$\sum _{j=0}^{\infty }\frac{{\lambda }^j{e}^{-\lambda }}{j!}=1$$

因此，

$$\mathbb{E}(X)=\lambda \cdot 1=\lambda$$

方差

方差（Variance）表示随机变量与其期望值之间的离散程度。方差的定义为：

$$\text{Var}(X)=\mathbb{E}[(X-\mathbb{E}(X){)}^2]=\mathbb{E}(X^2)-(\mathbb{E}(X){)}^2$$

首先，我们计算 ( \mathbb{E}(X^2) )。利用泊松分布的性质，定义二阶矩：

$$\mathbb{E}(X^2)=\sum _{k=0}^{\infty }{k}^2\cdot P(X=k)$$

代入泊松分布的概率质量函数：

$$\mathbb{E}(X^2)=\sum _{k=0}^{\infty }{k}^2\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}$$

我们可以将 ( k^2 ) 分解为 ( k(k-1) + k )：

$$\mathbb{E}(X^2)=\sum _{k=0}^{\infty }(k(k-1)+k)\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}$$

拆开求和：

$$\mathbb{E}(X^2)=\sum _{k=0}^{\infty }k(k-1)\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}+\sum _{k=0}^{\infty }k\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}$$

对于第一项，令 ( j = k-2 )：

$$\sum _{k=0}^{\infty }k(k-1)\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}={\lambda }^2\sum _{j=0}^{\infty }\frac{{\lambda }^j{e}^{-\lambda }}{j!}={\lambda }^2$$

对于第二项，我们已经知道：

$$\sum _{k=0}^{\infty }k\cdot \frac{{\lambda }^k{e}^{-\lambda }}{k!}=\lambda$$

因此，

$$\mathbb{E}(X^2)={\lambda }^2+\lambda$$

代入方差公式：

$$\text{Var}(X)=\mathbb{E}(X^2)-(\mathbb{E}(X){)}^2={\lambda }^2+\lambda -{\lambda }^2=\lambda$$

结论

对于泊松分布
，其期望值和方差分别为：

$$\mathbb{E}(X)=\lambda$$

$$\text{Var}(X)=\lambda$$

这些结果表明，在固定时间间隔内某事件发生的次数的平均值是 ( \lambda )，而离散程度也由 ( \lambda ) 决定。

这篇关于证明 泊松分布 的期望和方差的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---