证明专题
一种极简的余弦定理证明方法
余弦定理的证明方法有很多种,这里介绍一种极简的证明方法。该方法是本人在工作中推导公式,无意中发现的。证明非常简单,下面简单做下记录。 如上图为任意三角形ABC,以点C为原点,建立直角坐标系(x轴方向任意,y轴与x轴垂直),x轴与CB夹角为 θ 1 \theta_1 θ1,x轴与CA夹角为 θ 2 \theta_2 θ2。点B的坐标为 ( a c o s θ 1 , a s i n θ
零知识证明-ZK-SNARKs基础(七)
前言 这章主要讲述ZK-SNARKs 所用到的算术电路、R1CS、QAP等 1:算术电路 算术运算电路 1>半加器:实现半加运算的逻辑电路 2>全加器:能进行被加数,加数和来自低位的进位信号相加,并根据求和结果给出该位的进位信号 说明:2进制加,低位进位 相当于 结果S为 = A+B+C(地位进位) 高位进位 = A+B+C(地位进位) 三个中 有最少2个为1 高位就有进位了 【1】 方程转算
云WAF在安全审计和合规性证明方面起到什么作用?
云WAF在安全审计和合规性证明方面起到什么作用? 云WAF的基本功能 云WAF(Cloud Web Application Firewall)是一种部署在云端的网络安全解决方案,它能够为Web应用程序提供强有力的保护,通过检测和阻止恶意流量、攻击和漏洞,确保Web应用程序的安全性和可用性。云WAF具备访问控制、网络安全审计、漏洞检测、应用安全保护、数据安全监控和审计等功能,这些功能共同构成了一
安全多方计算 同态密文计算 零知识证明 是什么、对比、优缺点
基于计算困难性理论的安全多方计算可以进一步细分为基于混淆电路的方案或者基于秘密分享的方案。 基于混淆电路的方案将所需计算的函数表达成一个巨型的布尔电路,例如,目前表达一次 SHA-256 计算至少需要使用 13 万个布尔门。尽管学术界已经提供了大量优化方案,通用 电路转化的过程依旧很复杂。由于需要使用不经意传输技术来安全地提供电路输入,即便 在有硬件加速的条件下,这类方案的处理吞吐量和计算效率依
再次拿下品牌全球代言人,王鹤棣商业价值再度证明!
9月2日,FENTY BEAUTY品牌正式官宣王鹤棣为全球代言人,这也是该品牌创立至今官宣的中国首位全球代言人。 FENTY BEAUTY是由美国歌手Rihanna创立于2017年的高端美妆品牌,也是LV母公司LVMH集团联手RIHANNA一同孵化的品牌,因其产品具有强包容性,以及能满足消费者多元需求,获得了国际声誉和市场高度认可,品牌全球吸金力排在集团第一梯队,已连年被纳入LVMH集团
使用单个位来存放每个结点的颜色:证明与实现
使用单个位来存放每个结点的颜色:证明与实现 背景知识问题阐述BFS算法的伪代码修改后的BFS算法的伪代码证明过程C语言实现结论 在算法和图论中,染色问题是一个重要的话题,尤其是在处理诸如二分图检测、图的遍历等问题时。本文将探讨在使用广度优先搜索(BFS)算法时,为何仅使用单个位来存放每个结点的颜色即可,并通过详细证明及C语言代码实现来阐述这一点。 背景知识 在图论中,图的遍
【零知识证明】通读Tornado Cash白皮书(并演示)
1 Protocol description 协议描述有以下功能: 1.insert:向智能合约中存入资金,通过固定金额的单笔交易完成,金额由N表示(演示时用1 ETH) 2.remove:从智能合约中提取资金,交易由收款人发起,收款人应该有足够的以太币支付gas费,在这种情况下费用为0(无中继者) 在演示案例中,将实现存款功能和提款功能,无论谁调用提款函数都将是收款人 1.1 Setu
零知识证明-椭圆曲线(四)
前言 零知识证明(Zero—Knowledge Proof),是指一种密码学工具,允许互不信任的通信双方之间证明某个命题的有效性,同时不泄露任何额外信息 上章介绍了基础数字知识,这章主要讲 椭圆曲线 方程 2:椭圆曲线方程 y2+axy+by=x3+cx2+dx+e 式中,a、b、c、d、e均为实数,x和y在实数集上取值。 在加密领域一般采用如下简化后的数学形式: 有限域椭圆曲线 y2= x3+
【零知识证明】构建第一个zk
1 必要步骤 视频学习:5. Circcom 中的基本算术电路_哔哩哔哩_bilibili 文字学习:https://hackmd.io/@YlNLZS2ESI21OSqdTW_mPw/S1jqN-h80/edit 第五课,circom实践,需要安装 1 vscode 2 rust:Windows安装Rust环境(详细教程)-CSDN博客 安装rust出现问题解决方案:Wind
manim动画:利用极限的定义证明极限。
函数的证明 用极限的定义来证明下面的极限。 要用极限的定义证明 ,我们可以使用极限的定义: 设f(x)在包含a的开区间中对所有x≠a有定义,设L为实数。然后 如果,任意一个,存在一个 ,以至于如果对于所有x在f的定义域内,然后 用定义我们得到:, 同时 要用极限的定义证明 ,我们可以使用极限的定义:对任意的,存在 ,使得当 时,有 ,其中 和 。 证
《大道平渊》· 拾捌 —— 证明自己,本身就毫无意义。
《大道平渊》 我在任何时候都会保持最轻松的状态,选择最舒适的态度和动作。 我在与人交谈时,无论何时何地,都会像在家里躺着和挚友交谈一样轻松。 我总是悠然自若,因为我深知自己的过度表现,只会给人留下怪异的印象。 我从不向他人寻求价值,而是极力发觉自身价值。 我从不为我的失误解释,因为没有必要对错误进行修饰。 我也不想与他人争辩,因为我根本不在乎争论的输赢。 我甚至不需要他人认可和理
【初阶数据结构】链表题的证明
环形链表题目方法的证明 证明1:为什么快指针每次⾛两步,慢指针⾛⼀步可以相遇,有没有可能遇不上,请推理证明! 证明二:为什么相遇点(meet)和头结点(head)到入环结点的距离是相等的
并查集优化策略及其正确性证明:基于路径压缩与按秩合并
并查集优化策略及其正确性证明:基于路径压缩与按秩合并 前言优化策略算法伪代码C语言实现归纳法证明基础情况归纳步骤 结论 前言 引理:对于所有的结点x, 有 x.rank≤x.p.rank, 如 果x≠x.p, 则此式是严格不等 式。x.rank 的初始值为0,并且随时间而增加,直到x≠x.p; 从此以后,z.rank 的值就不再发 生变化。x.p.rank 的值随时间单调递增。这
加密学中的零知识证明(Zero-Knowledge Proof, ZKP)到底是什么?
加密学中的零知识证明(Zero-Knowledge Proof, ZKP)到底是什么? 引言 在加密学的应用中,零知识证明(Zero-Knowledge Proof, ZKP)无疑是一颗璀璨的明星。它不仅挑战了我们对信息验证的传统认知,更在保护隐私的同时确保了数据的真实性,为数字货币、身份验证、安全通信等多个领域带来了革命性的变革。本文将深入探讨零知识证明的原理、关键技术、应用场景以及未来
kruskal求得的生成树是最小生成树的证明
kruskal求得的生成树是最小生成树的证明 给一带权连通的树一定会有至少一棵生成树,那么这些生成树中间必然会会存在至少一棵最小生成树。 假设T是用kruskal求出来的最小生成树,而U是这个图的最小生成树,如果U == T,那么证明结束。 然而如果T != U,那么至少存在一条边在T中,不在U中。那么我们希望证明T和U中所有边的权值之和是相等的。假设存在k条边存在T中不存在U
关于快速幂算法有效性的证明
在读这篇文章之前,请确保已经完全明白二进制基础以及其他与本文相关的二进制的知识 首先,假设我们要求,设a=3,b=101将b转化为二进制表示,则为:1100101通过二进制基础,我们知道:,通过乘法原理,我们知道:,因此,可以推出:那么,我们想象一下:如果计算(设x为任意数)的时间复杂度为O(1),则计算的时间复杂度就成为了O(6),也就是也就是说,计算的时间复杂度也就成为了 那么,接下来
某大厂程序员吐槽:离职交接时,新人被工作量吓退,领导却污蔑我故意劝退新人,我怒晒工作短信反击证明,新人看了后也决定走人了!
一位知名大公司的程序员分享了他离职时的遭遇:在交接工作时,新进的同事因工作量过大而感到压力,但出乎意料的是,他们的领导却指责我故意吓唬新人。为了证明自己的清白,我晒出了工作短信作为反击,结果连新人也决定离开。 在任何组织里,团队文化的优劣都是决定工作效率和质量的关键。一个和谐相处的团队不仅能提升工作效率,还能使工作氛围变得轻松愉快。 然而,一旦团队内部出现权力斗争或领导偏爱小团体、
【PL理论深化】(3) MI 归纳法:归纳假设 (IH) | 结构归纳法 | 归纳假设的证明
💬 写在前面:所有编程语言都是通过归纳法定义的。因此,虽然编程语言本身是有限的,但用该语言编写的程序数量是没有限制的,本章将学习编程语言研究中最基本的归纳法。本章我们继续讲解归纳法,介绍归纳假设和结构性归纳法。 目录 0x00 归纳假设 (IH) 和结构归纳法 0x01 归纳假设的证明 0x00 归纳假设 (IH) 和结构归纳法 归纳法是一种用于证明归纳定义的集合中的元素所具有
3、如何证明static静态变量和类无关?
如何证明static静态变量和类无关? 可以从以下三个方面证明static静态变量和类无关; 1、不需要初始化类就可以直接使用静态变量; 2、在类中写个main方法运行,即便不写初始化类的代码,静态变量都会自动初始化; 3、静态变量只会初始化一次,初始化完成之后,不管再new多少个类出来,静态变量都不会再初始化。 不仅仅是静态变量,静态方法块也和类无关。
(一篇Blog证明还在地球)论文精读:基于CLIP引导学习的多模态虚假新闻检测
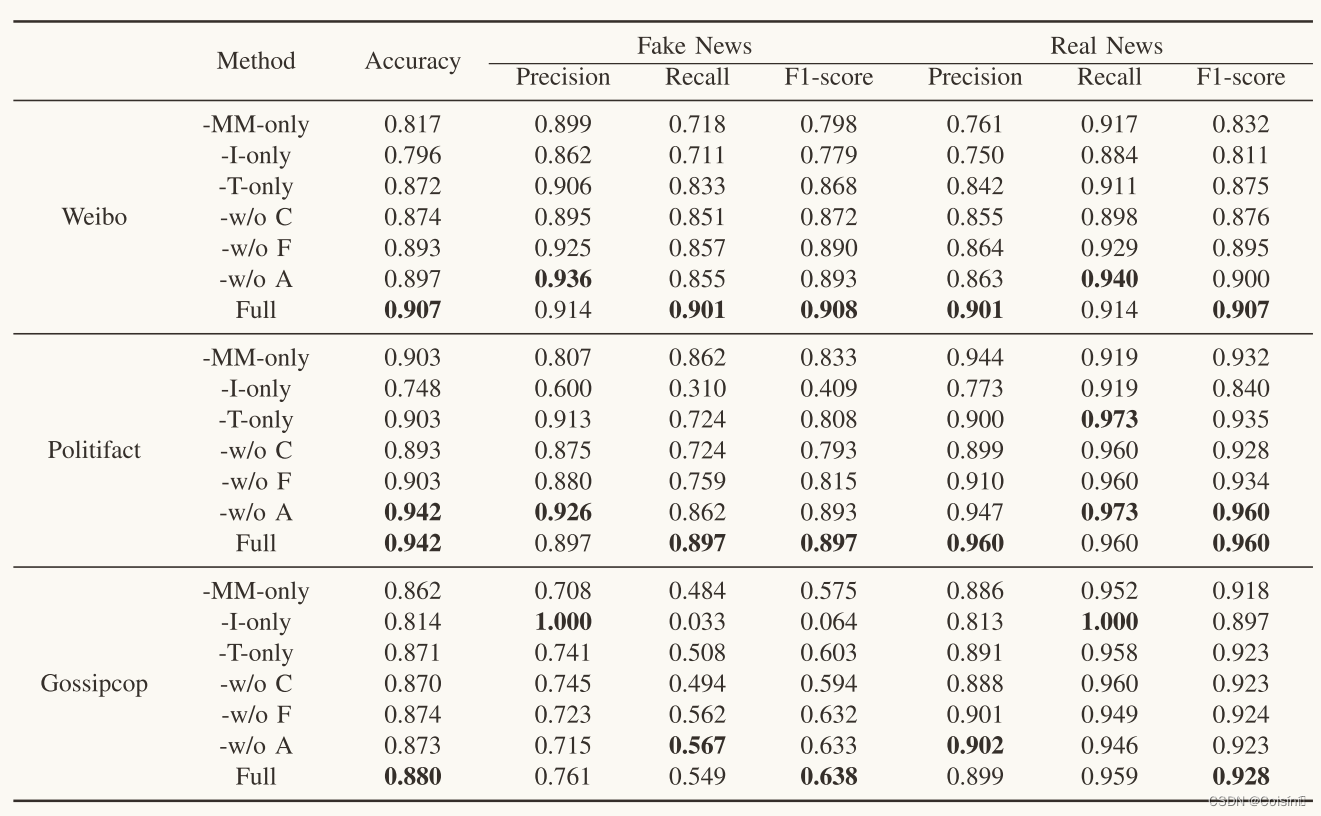
摘要 假新闻检测在社会取证领域引起了广泛的研究兴趣。许多现有的方法引入了定制的注意机制来融合单峰特征。然而,它们忽略了模式之间的跨模式相似性的影响。同时,预训练的多模式特征学习模型在FND中的潜力还没有得到很好的开发。这篇论文提出了一种FND-CLIP框架,即基于对比语言图像预训练(CLIP)的多模式假新闻检测网络。FND-CLIP使用两个单峰编码器和两个成对的CLIP编码器一起从新闻中提取深层
【区块链】POS(Proof of Stake)权益证明算法深度解析
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 POS(Proof of Stake)权益证明算法深度解析引言1. POS基本概念1.1 定义1.2 工作原理 2. POS的关键机制2.1 币龄与随机选择2.2 利息与通胀控制2.3 安全性与攻击
证明 几何分布 的期望和方差
几何分布 几何分布(Geometric Distribution)描述了在进行一系列独立的伯努利试验时,第一次成功所需的试验次数。假设每次试验成功的概率为 ( p ),则几何分布的概率质量函数(PMF)为: P ( X = k ) = ( 1 − p ) k − 1 p , k = 1 , 2 , 3 , … P(X = k) = (1 - p)^{k-1} p, \quad k = 1,
证明 泊松分布 的期望和方差
泊松分布 泊松分布(Poisson Distribution)是描述在固定时间间隔内某事件发生次数的概率分布,特别适用于稀有事件的统计。假设随机变量 ( X ) 表示在时间间隔 ( t ) 内某事件发生的次数,并且该事件在单位时间内发生的平均次数为 ( \lambda )。那么 ( X ) 服从参数为 ( \lambda ) 的泊松分布,记作 泊松分布的概率质量函数(PMF)为: P (
HDU2552_三足鼎立【数学证明】
三足鼎立 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 2418 Accepted Submission(s): 1344 Problem Description MCA山中人才辈