泊松专题
概率论(二)-随机变量及其分布:分布函数F(x)、离散型随机变量【分布律:(0-1)分布、二项分布、泊松分布】、连续型随机变量【概率密度:均匀分布、指数分布、正态/高斯分布】、3σ法则、偏度、峰度
1 随机变量 2 离散型随机变量及其分布律 3 随机变量的分布函数 4 连续型随机变量及其概率密度 5 随机变量的函数的分布
证明 泊松分布 的期望和方差
泊松分布 泊松分布(Poisson Distribution)是描述在固定时间间隔内某事件发生次数的概率分布,特别适用于稀有事件的统计。假设随机变量 ( X ) 表示在时间间隔 ( t ) 内某事件发生的次数,并且该事件在单位时间内发生的平均次数为 ( \lambda )。那么 ( X ) 服从参数为 ( \lambda ) 的泊松分布,记作 泊松分布的概率质量函数(PMF)为: P (
ZOJ 3696 Alien's Organ / 泊松分布
有遇到 奇葩的 前所未闻的东西 记一下 观察事物平均发生m次的条件下,实际发生x次的概率P(x) p(k)=(y^k) / (k!) * e^(-y) 吊炸天 这种东西做梦都想不到 平均每天生产的λ 个,每天生产不超过n的可能性 代码参考别人的 #include <cstring>#include <cstdio>#include <cmath>int main(){int T
泊松分布与指数分布的理解
说到泊松分布,最好是明白:泊松分布是二项分布n很大而p很小时的一种极限形式。 二项分布:已知某件事情发生的概率是p,那么做n次试验,事情发生的次数就服从二项分布。 泊松分布式某段连续的时间内事情发生的次数。事情发生的时间是可以忽略的。关注的是事件的发生。泊松分布是离散的变量。 这段时间是确定大小的,不是说某两件事件(不知何时发生)的间隔。 把连续的时间分割层无数小份,那么每个小份之间都是相
NumPy 泊松分布模拟与 Seaborn 可视化技巧
泊松分布 简介 泊松分布是一种离散概率分布,用于描述在给定时间间隔内随机事件发生的次数。它常用于模拟诸如客户到达商店、电话呼叫接入中心等事件。 参数 泊松分布用一个参数来定义: λ:事件发生的平均速率,表示在单位时间内事件发生的平均次数。 公式 泊松分布的概率质量函数 (PMF) 给出了在指定时间间隔内发生 k 次事件的概率,计算公式为: P(k) = e^(-λ) (λ^k) /
二维泊松方程(Neumann+Direchliet边界条件)有限元Matlab编程求解|程序源码+说明文本
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元类型包含:杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,壳单元,四/六面体实体单元,金字塔单元等;3.物理场问题涉及:力学、传热学、电磁学及多物理场耦合等问题的稳态(静力学)和瞬态(动力学)
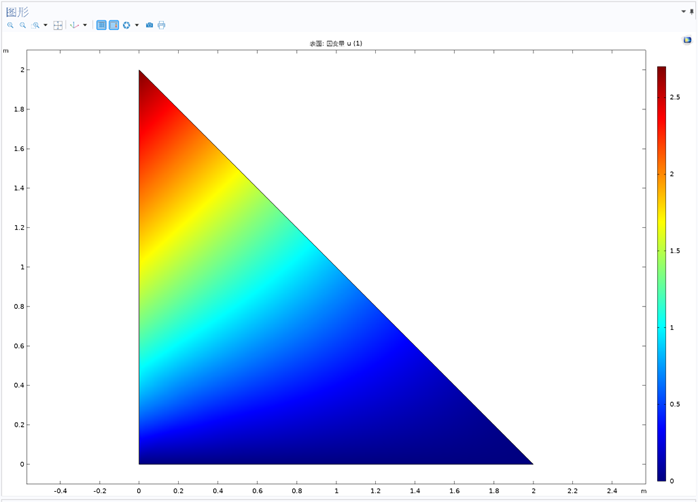
二维泊松方程(三角形区域)Matlab有限元编程求解|案例源码+说明文本
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元类型包含:杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,壳单元,四/六面体实体单元,金字塔单元等;3.物理场问题涉及:力学、传热学、电磁学及多物理场耦合等问题的稳态(静力学)和瞬态(动力学)
OpenCV源码解读:泊松融合seamlessClone(normalClone)
前言 泊松融合(Poisson Blending)是图像处理领域著名的图像融合算法,自从2003年发表以来,有很多基于此算法的应用和改进研究出现。泊松融合无需像Alpha blending一样的精确抠图就可以得到很自然的结果。 关于泊松融合原理部分的解析见之前的博客《泊松融合原理浅析》。 本文将针对OpenCV中泊松融合的实现代码(以normalClone为例)进行解读。 代码解读 函
2024年第十七届 认证杯 网络挑战赛 (B题)| 神经外科手术的定位与导航 | 有限元方法 泊松分布 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 让我们来看看认证杯 网络挑战赛 (B题)! CS团队倾注了大量时间和心血,深入挖掘解决方案。通过有限元方法、泊松分布等算法,设计了明晰的项目,耗费时间确保可行性。为客户选择了最适项目,以数据支持、文献分析和可视化手段深刻展示思路。这
python实现泊松回归
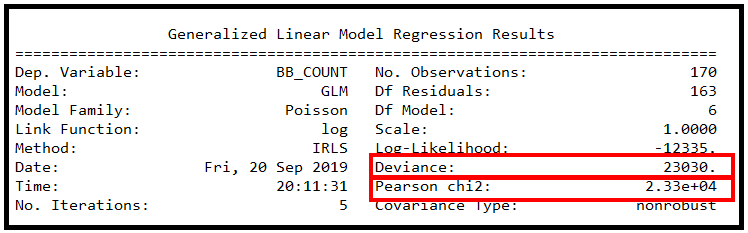
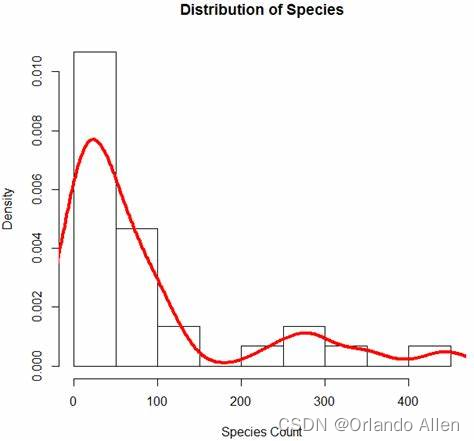
1 什么是基于计数的数据? 基于计数的数据包含以特定速率发生的事件。发生率可能会随着时间的推移或从一次观察到下一次观察而发生变化。以下是基于计数的数据的一些示例: 每小时穿过十字路口的车辆数量每月去看医生的人数每月发现的类地行星数量 计数数据集具有以下特征: 整数数据:数据由非负整数组成:[0… ∞] 。普通最小二乘回归等回归技术可能不适合对此类数据进行建模,因为 OLSR 最适
R语言进行数值模拟:模拟泊松回归模型的数据
模拟回归模型的数据 验证回归模型的首选方法是模拟来自它们的数据,并查看模拟数据是否捕获原始数据的相关特征。感兴趣的基本特征是平均值。我喜欢这种方法,因为它可以扩展到广义线性模型(logistic,Poisson,gamma,...)和其他回归模型,比如t -regression。这是Gelman和Hill在回归文本中的内容。1可悲的是,从R中回归模型模拟数据的默认方法错过什么人可能会考虑模型不确
应用回归分析:泊松回归
泊松回归是一种广泛用于计数数据的回归分析方法。它适用于响应变量是非负整数的情况,特别是当这些计数呈现出明显的离散分布时。泊松回归通过泊松分布的概率分布函数来建模计数数据,使其成为处理计数数据的自然选择。本文将介绍泊松回归的基本概念、应用场景、优缺点以及如何实施。 基本概念 泊松回归基于泊松分布的假设,泊松分布是一种描述在固定时间或空间内发生某事件次数的概率分布。泊松回归模型的形式通常表示为
MATLAB知识点:poissrnd函数(★★☆☆☆)生成泊松分布的随机数
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 节选自第3章:课后习题讲解中拓展的函数 在讲解第三章课后习题的过程中,我给大家拓展了一些讲义中没有介绍的新函数: (14)poissrnd函数(★★☆☆☆) poissrnd函数用于生成泊松分
R语言贝叶斯Metropolis-Hastings Gibbs 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间
最近我们被客户要求撰写关于吉布斯采样的研究报告,包括一些图形和统计输出。 指数分布是泊松过程中事件之间时间的概率分布,因此它用于预测到下一个事件的等待时间,例如,您需要在公共汽车站等待的时间,直到下一班车到了。 在本文中,我们将使用指数分布,假设它的参数 λ ,即事件之间的平均时间,在某个时间点 k 发生了变化,即: 我们的主要目标是使用 Gibbs 采样器在给定来自该分布的
R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间...
原文链接:http://tecdat.cn/?p=26578 指数分布是泊松过程中事件之间时间的概率分布,因此它用于预测到下一个事件的等待时间,例如,您需要在公共汽车站等待的时间,直到下一班车到了(点击文末“阅读原文”获取完整代码数据)。 相关视频 在本文中,我们将使用指数分布,假设它的参数 λ ,即事件之间的平均时间,在某个时间点 k 发生了变化,即: 我们的主要目标是使用 Gibbs
高斯噪声和泊松噪声的最大后验模型去噪
文章目录 1. 高斯噪声的最大后验去噪模型1.1 退化模型1.2 最大后验建模 2.泊松噪声的最大后验去噪模型 1. 高斯噪声的最大后验去噪模型 1.1 退化模型 高斯噪声的数学模型如(1)式所示 y = x + n (1) y=x+n \tag{1} y=x+n(1) 其中 y y y是噪声图像, x x x是清晰图像, n n n为加性高斯噪声服从独立同分布(i.i.
HashMap defaultLoadFactor = 0.75和泊松分布没有关系
很多人说HashMap的DEFAULT_LOAD_FACTOR = 0.75f是因为这样做满足泊松分布,这就是典型的半知半解、误人子弟、以其昏昏使人昭昭。实际上设置默认load factor为0.75和泊松分布没有关系,随机哈希的存放数据方式本身就是满足泊松分布的。 java8及以上版本中开头这一段的注释,是为了解释在java8 HashMap中引入Tree Bin(也就是放数据的每个数组bin
HashMap默认负载因子0.75和泊松分布有关系吗?
我们在看HashMap源码时,知道HashMap默认的负载因子是0.75。那这个0.75是怎么来的呢? /*** The load factor used when none specified in constructor.*/static final float DEFAULT_LOAD_FACTOR = 0.75f; 通常,加载因子需要在时间和空间成本上寻求一种折衷。 加载因子过高
人工智能数学基础--概率与统计10:离散随机变量的概率函数及常见的二项分布、泊松分布
一、离散随机变量的概率函数及分布函数 设X为离散随机变量,其全部可能取值为{a1,a2,…},则:pi=P(X=ai) (i=1,2,…)称为X的概率函数,也称为随机变量X的概率分布; 设X为随机变量(包括离散和非离散),则函数:P(X≤x) = F(x) (-∞ < x <∞) 称为X的分布函数; 结合概率函数和分布函数的定义,对于离散随机变量,有: P(i) = P(X=i)
聚电解质微凝胶的泊松-玻尔兹曼-弗洛里理论
参考文献:J. Chem. Phys. 141, 234902 (2014) 聚电解质微凝胶由\(N\)条链组成,每条链链长为\(m\),链带电分率为\(\alpha\),电离出反离子数目为\(Z=fNm\)。微凝胶半径为\(a\)。溶液中平均每个凝胶占据的体积为\(\frac{4\pi}{3}R^3\) 体系自由能(以\(k_BT\)约化)为: \begin{equation} \begi
泊松图像编辑/融合(Possion image editing)的原理与数值解算法
泊松图像融合是目前融合算法的标杆,泊松图像编辑不仅可以用于图像融合,还可以用于风格迁移、插入透明物体、局部亮度/颜色调制等。网上有不少介绍泊松图像融合算法的文章,但基本表都刻意淡化了其理论推导,着重去讲其实现,让人读完还是只知其然而不知其所以然,甚至连知其然都做不到。这里我将尝试从原理到实现系统地讲一讲泊松图像编辑/融合技术。(注:本文源于对http://www.ipol.im/pub/art/2