泊松图像编辑/融合（Possion image editing）的原理与数值解算法

泊松图像融合是目前融合算法的标杆，泊松图像编辑不仅可以用于图像融合，还可以用于风格迁移、插入透明物体、局部亮度/颜色调制等。网上有不少介绍泊松图像融合算法的文章，但基本表都刻意淡化了其理论推导，着重去讲其实现，让人读完还是只知其然而不知其所以然，甚至连知其然都做不到。这里我将尝试从原理到实现系统地讲一讲泊松图像编辑/融合技术。（注：本文源于对http://www.ipol.im/pub/art/2016/163/上“Possion image editing”论文与源码的解读，读者可以自行从上面下载论文和代码）

泊松图像编辑的原理说来也不复杂，其实就是在满足一定边界的条件下让待求解二维函数在区域中的梯度场与参考梯度场尽可能相似，这种相似度最大化用差值的二阶范数最小化来表征，而这个边界条件就是函数值在边界上与目标图像的的取值相等，这就是所谓的狄利克雷边界条件。用数学方式表示就是：

 其解满足欧拉——拉格朗日方程：

该方程就是所谓的泊松方程。关于散度的理解可以参考https://blog.csdn.net/weixin_41923961/article/details/85225757。对于与图像外边缘相交的特殊情况<注：对此特殊况不感兴趣的可以直接跳过>，狄利克雷边界条件被上的纽曼边界条件（即边界处导数为0）替代，也就是相当于对图像进行了边缘复制性外扩。

前述泊松方程的矩阵表示为：

 其中，、的形式与我先前的博客https://blog.csdn.net/u014230360/article/details/107639764里的相似，但以外区域的对应行都是零值行！、、分别是待求解图像、参考梯度场x分量、参考梯度场y分量的向量化表示。以一个4*4的图像示意，拉普拉斯矩阵的形式如下图所示（第一行两个1的外框颜色反了，图是从论文中截取的）。

也就是说，L在与图像外边缘不相交的时候，中对应于的每一行的非零元素都是1、1、-4、1、1（注意，是对应于的行才是非零行！）。当出现与图像外边缘相交的特殊情况时，由于交集上的点的像素值由上的点的像素值复制而来，此时中对应坐标的值被替代，也就出现了上图中的情况。

记的投影矩阵如下式所示（N=H*W，等于<边界外扩后的>图像的总像素数）：

 即只有对应中某点的行在主对角线上有一个值1，其他行均为零值行。

 同样，记的外边界的投影矩阵为：

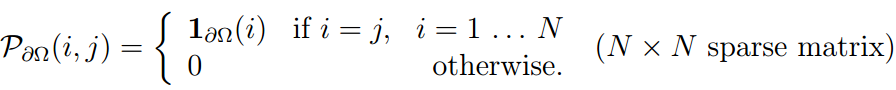
记对中点进行采样的采样矩阵为：

 对、、的解释见下图（注意图中边界的外扩！）：

于是有,继而有：

最后一步中还是一个关于N个未知数的N维方程组，但实际上真正与问题相关的的未知数只有n个（n对应中的像素点数)。用采样矩阵作用于其上，得：

其中，是对应于 中像素点的nx1的列向量。

以上便是用于求解目标图像中像素值的形如的方程。解出,用对应的值取代目标图像中的相应值即完成泊松编辑。

当区域是一个矩形区域时，关于泊松方程的求解还有一个更高效的基于傅里叶变换的实现，以后有时间我再讲一讲。感兴趣的同学暂时可以参照http://www.ipol.im/pub/art/2016/163/的论文和代码自行研究。

效果图就不放了，网上一搜一大堆，论文中也多的是。