本文主要是介绍python实现泊松回归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 什么是基于计数的数据?
基于计数的数据包含以特定速率发生的事件。发生率可能会随着时间的推移或从一次观察到下一次观察而发生变化。以下是基于计数的数据的一些示例:
- 每小时穿过十字路口的车辆数量
- 每月去看医生的人数
- 每月发现的类地行星数量
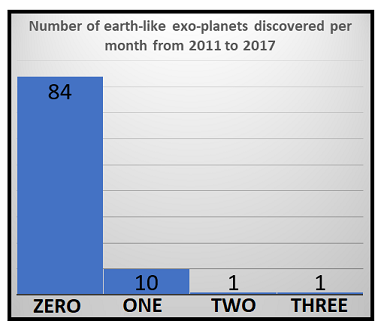
计数数据集具有以下特征:
- 整数数据:数据由非负整数组成:[0… ∞] 。普通最小二乘回归等回归技术可能不适合对此类数据进行建模,因为 OLSR 最适合实数,例如 -656.0、-0.00000345、13786.1 ETC。
- 偏斜分布:数据可能包含少量值的大量数据点,从而使频率分布相当偏斜。请、参见上面的直方图示例。
- 稀疏性:数据可能反映了伽马射线爆发等罕见事件的发生,从而使数据变得稀疏。
- 发生率:为了创建模型,可以假设事件 λ 有一定的发生率来驱动此类数据的生成。事件发生率可能会随着时间的推移而发生变化。
下表包含在纽约市各桥梁上骑行的骑自行车者的计数。从2017年4月1日到2017年10月31日,每天都会测量计数。
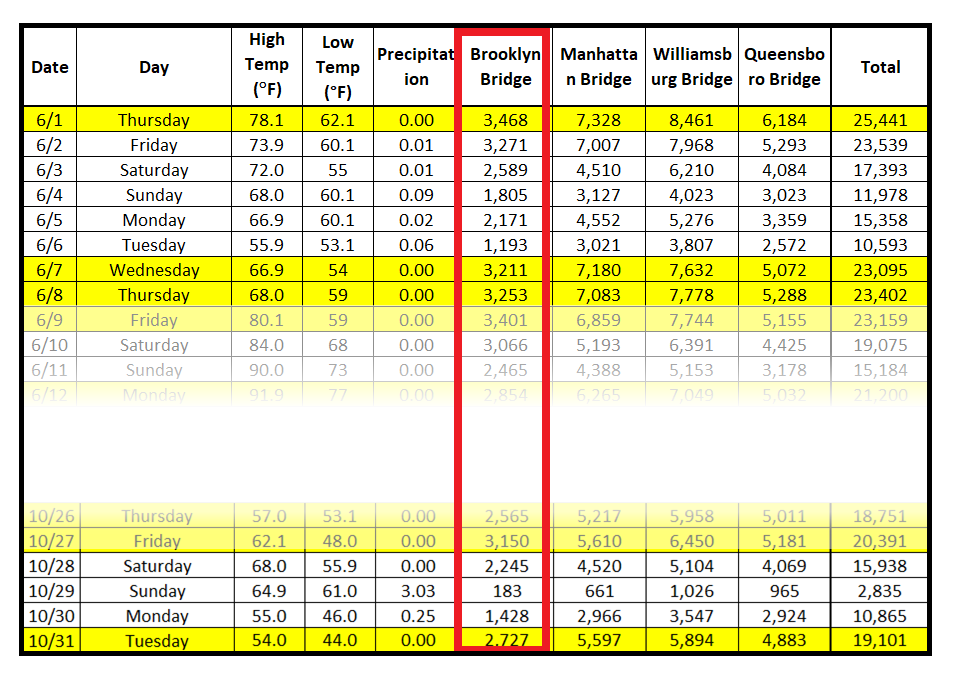
以下是布鲁克林大桥上骑自行车的人计数的时间顺序图:
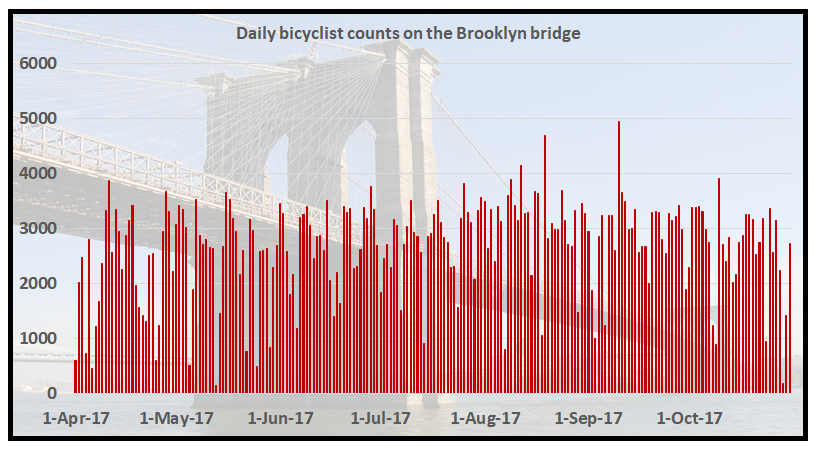
2 计数回归模型
泊松回归模型和负二项式回归模型是开发计数回归模型的两种流行技术。其他可能包括有序 Logit、有序 Probit 和非线性最小二乘模型。
最好从泊松回归模型开始,并将其用作更复杂或约束较少的模型的“控制”。卡梅伦和特里维迪在他们的**《计数数据回归分析》**一书中说道:
“一个合理的做法是估计泊松模型和负二项式模型。”
在本节中,将使用泊松回归模型对布鲁克林大桥上观察到的骑自行车者计数进行回归。
3 泊松模型简介
泊松分布具有以下概率质量函数。
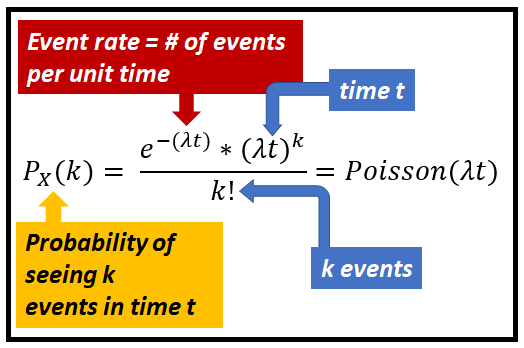
泊松分布的期望值(平均值)是 λ。因此,在缺乏其他信息的情况下,人们应该期望在任何单位时间间隔(例如 1 小时、1 天等)内看到 λ 事件。对于任何时间间隔 t,人们都期望看到 λt 事件。
- 常数 λ 的泊松回归模型
如果事件发生率 λ 是恒定的,则可以简单地使用修改的平均模型来预测未来的事件计数。在这种情况下,可以将所有计数的预测值设置为该恒定值 λ。
下图说明了常数 λ 的场景:

- 非常数 λ 的泊松回归模型
检查一种更常见的情况,其中 λ 可以从一个观察值更改为下一个观察值。在这种情况下,假设 λ 的值受到解释变量向量(也称为预测变量、回归变量或回归变量)的影响,将这个回归变量矩阵称为 X。
回归模型的作用是将观察到的计数 y 拟合到回归值矩阵 X 。
在纽约市骑自行车者计数数据集中,回归变量为日期、星期几、高温、低温和降水量。还可以引入额外的回归量,例如从日期派生的月份和日期,并且可以自由地删除现有的回归量,例如日期:
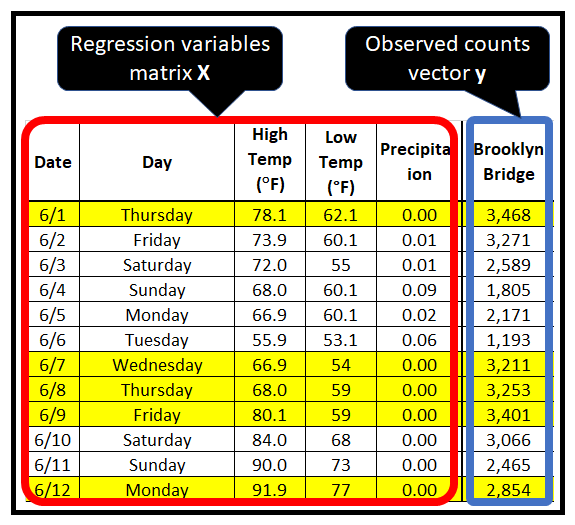
y 与 X 的拟合是通过固定回归系数 β 向量的值来实现的。
在泊松回归模型中,事件计数 y 被假定为泊松分布,这意味着观察 y 的概率是事件率向量 λ 的函数。
泊松回归模型的工作是通过链接函数将观测计数 y 拟合到回归矩阵 X,该链接函数将速率向量 λ 表示为回归系数 β 和 回归矩阵 X 的函数。
下图说明了泊松回归模型的结构。
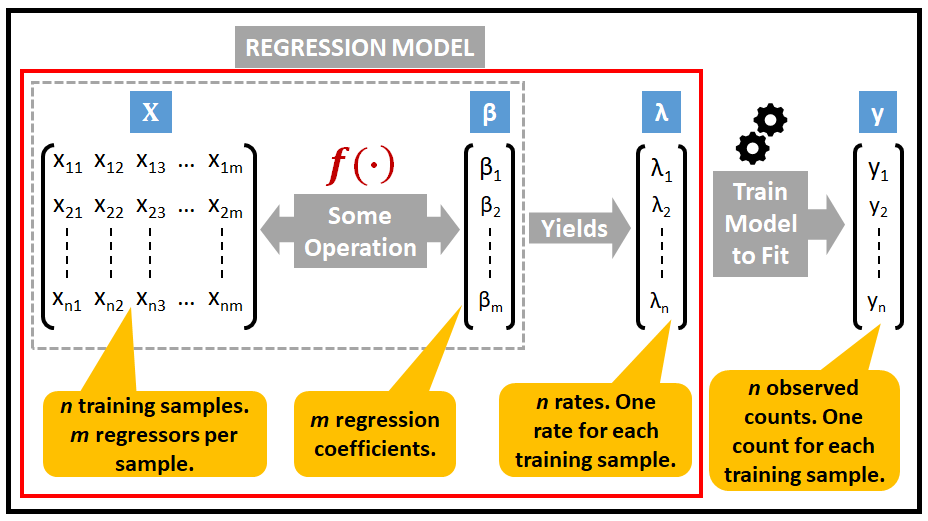
将 λ 与 X 连接起来的良好链接函数 f(.) 是什么?事实证明,以下指数链接函数效果很好:
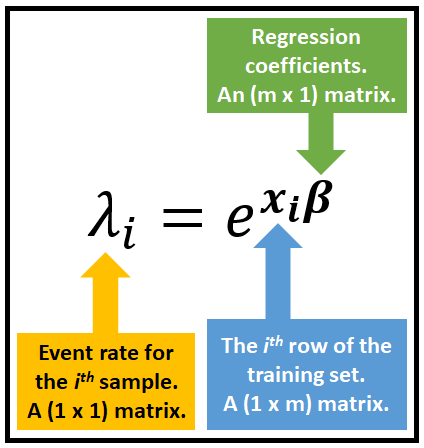
即使当回归量 X 或回归系数 β 具有负值时,该链接函数也使** λ 保持非负值**。这是基于计数的数据的要求。
一般来说,有:

4 泊松回归模型的形式化说明
基于计数的数据的泊松回归模型的完整规范如下:
对于数据集中由 y_i 表示的与回归变量 x_i 行对应的第 i 个观测值,观测计数 y_i 的概率是按照以下 PMF 的泊松分布:

其中第 i 个样本的平均速率 λ_i 由前面所示的指数链接函数给出。在这里重现它:

一旦模型在数据集上得到充分训练,回归系数 β 就已知,模型就可以进行预测了。为了预测与观察到的回归量 x_p 输入行相对应的事件计数 y_p,可以使用以下公式:
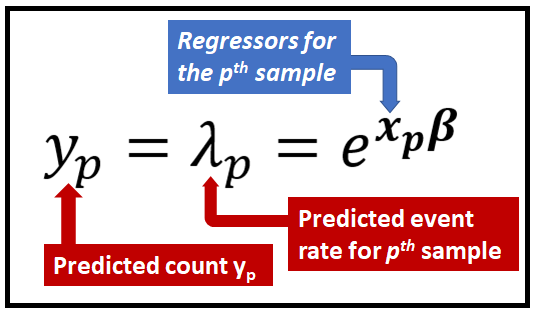
所有这些都取决于成功训练模型的能力,以便已知回归系数向量 β。
接下来看看这个训练是如何进行的。
5 训练泊松回归模型
训练泊松回归模型涉及查找回归系数 β 的值,这将使观察到的计数 y 的向量最有可能。
识别系数 β 的技术称为最大似然估计 (MLE)。
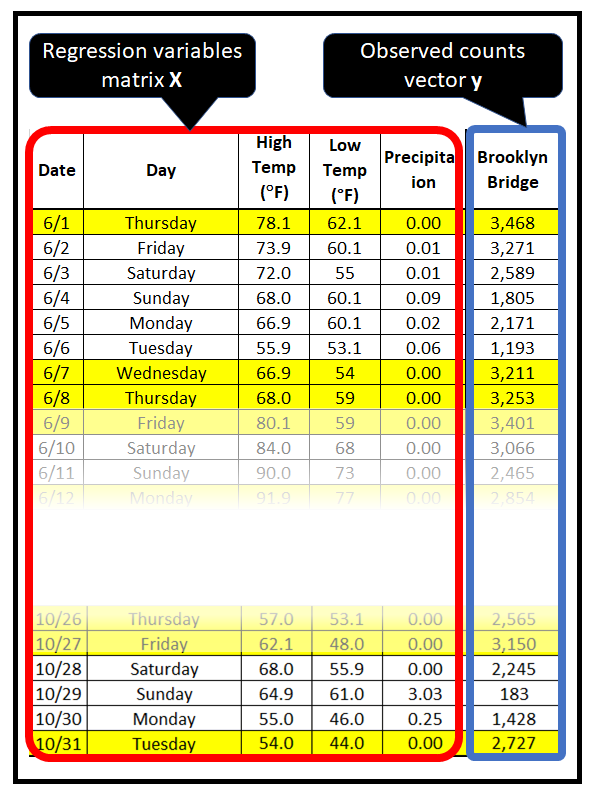
使用骑自行车者计数数据集来说明 MLE 技术。看一下该数据集的前几行:
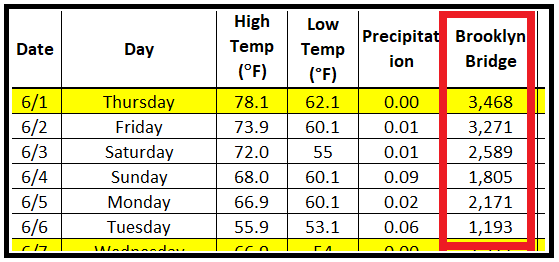
假设红框中显示的骑自行车者计数来自泊松过程。因此可以说它们发生的概率是由泊松 PMF 给出的。以下是前 4 次出现的概率:
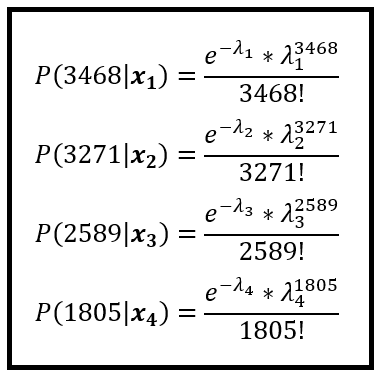
可以类似地计算训练集中观察到的所有 n 个计数的概率。
注意,在上面的公式中,λ_1,λ_2,λ_3,…,λ_n是使用link函数计算的,如下所示:

其中 x_1、x_2、x_3、x_4 是回归矩阵的前 4 行。
训练集中 n 个计数 y_1, y_2,…,y_n 的整个集合出现的概率是各个计数出现的联合概率。
计数 y 服从泊松分布,y_1, y_2,…,y_n 是独立的随机变量,相应地给出 x_1, x_2,…,x_n。因此,y_1、y_2、…、y_n 出现的联合概率可以表示为各个概率的简单乘法。以下是整个训练集的联合概率:
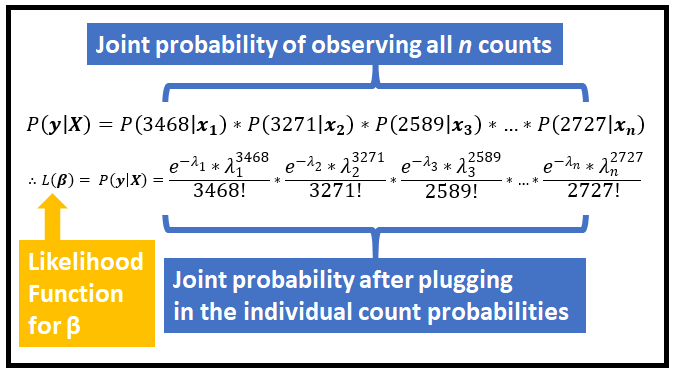
让我们回想一下,λ_1、λ_2、λ_3、…、λ_n 通过回归系数 β 链接到回归向量 x_1、x_2、x_3、…、x_n。
β 的什么值将使给定的观察计数 y 集最有可能出现?它是上式中所示的联合概率达到最大值时的β值。它是 β 的值,其中联合概率函数的对β的变化率为 0。换句话说,它是通过对联合概率方程对 β 进行微分而得到的方程的解并将该微分方程设置为 0。
联合概率方程的对数微分比原方程更容易。对数方程的解产生相同的 β 最优值。
这个对数方程称为对数似然函数。对于泊松回归,对数似然函数由以下等式给出:
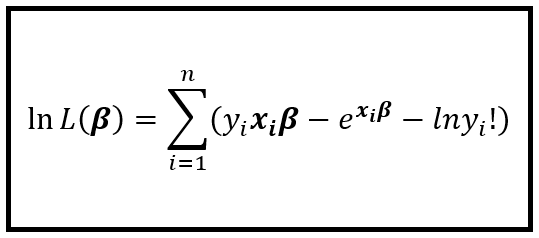
上式是将前面所示的联合概率函数两边取自然对数,并将 λ_i 替换为 exp(x_i*β) 后得到的。
如前所述,对数似然方程对 β 进行微分,并将其设置为零。这个运算提供了以下等式:
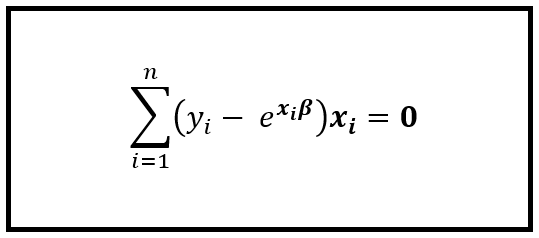
求解回归系数 β 的方程将得到 β 的最大似然估计 (MLE)。
为了求解上述方程,使用迭代方法,例如迭代重加权最小二乘法 (IRLS)。
6 执行泊松回归的步骤摘要
总之,以下是对基于计数的数据集执行泊松回归的步骤:
- 首先,确保数据集包含计数。一种判断方法是它仅包含非负整数值,表示某个时间间隔内某个事件发生的次数。在骑自行车者计数数据集中,它是每天穿过布鲁克林大桥的骑自行车者的数量。
- 找出(或猜测)会影响观察到的计数的回归变量。在骑自行车者计数数据集中,回归变量包括星期几、最低气温、最高气温、降水量等。
- 制定回归模型将用于训练的训练数据集,以及应保留的测试数据集。不要根据测试数据训练模型。
- 使用合适的统计软件(例如 Pythonstatsmodels 包)在训练数据集上配置和拟合泊松回归模型。
- 通过在测试数据集上运行模型来测试模型的性能,以生成预测计数。将它们与测试数据集中的实际计数进行比较。
- 使用拟合优度度量来确定模型在训练数据集上的训练效果。
7 如何在 Python 中训练泊松回归模型
目标是为观察到的骑车人计数 y 建立泊松回归模型。将使用经过训练的模型来预测模型在训练期间未见过的布鲁克林大桥上每日骑自行车的人数。
首先导入所有必需的包。
import pandas as pd
from patsy import dmatrices
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
为计数数据集创建一个 pandas DataFrame。
df = pd.read_csv('nyc_bb_bicyclist_counts.csv', header=0, infer_datetime_format=True, parse_dates=[0], index_col=[0])
我们将向 X 矩阵添加一些导出的回归变量。
ds = df.index.to_series()
df['MONTH'] = ds.dt.month
df['DAY_OF_WEEK'] = ds.dt.dayofweek
df['DAY'] = ds.dt.day
我们不会使用 Date 变量作为回归量,因为它包含绝对日期值,但我们不需要做任何特殊的事情来删除 Date,因为它已经被用作 pandas DataFrame 的索引。所以它在 X 矩阵中对我们来说是不可用的。
让我们创建训练和测试数据集。
mask = np.random.rand(len(df)) < 0.8
df_train = df[mask]
df_test = df[~mask]
print('Training data set length='+str(len(df_train)))
print('Testing data set length='+str(len(df_test)))
以 Patsy 表示法设置回归表达式。BB_COUNT 是因变量,它取决于回归变量:DAY、DAY_OF_WEEK、MONTH、HIGH_T、LOW_T 和 PRECIP。
expr = “”“BB_COUNT ~ DAY + DAY_OF_WEEK + MONTH + HIGH_T + LOW_T + PRECIP”“”
为训练和测试数据集设置 X 和 y 矩阵。 Patsy 让这一切变得非常简单。
y_train, X_train = dmatrices(expr, df_train, return_type='dataframe')
y_test, X_test = dmatrices(expr, df_test, return_type='dataframe')
使用 statsmodels GLM 类,在训练数据集上训练泊松回归模型。
poisson_training_results = sm.GLM(y_train, X_train, family=sm.families.Poisson()).fit()
打印总结。
print(poisson_training_results.summary())
这会打印出以下内容:
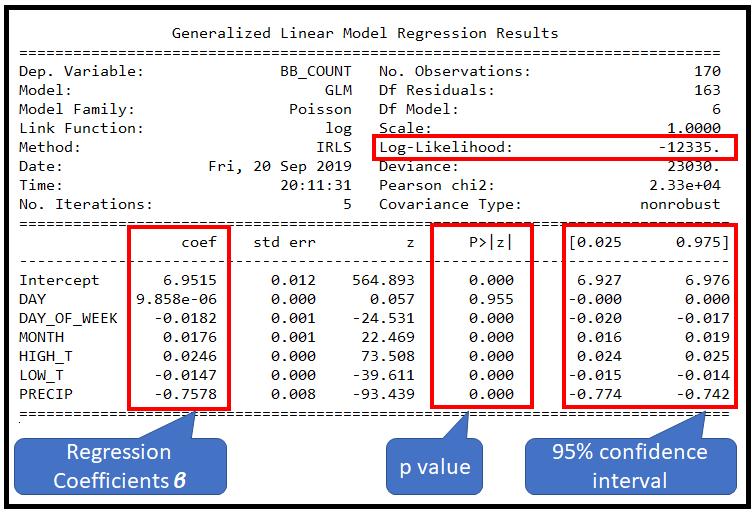
那么模型表现如何?对测试数据集做一些预测。
poisson_predictions = poisson_training_results.get_prediction(X_test)
#summary_frame() returns a pandas DataFrame
predictions_summary_frame = poisson_predictions.summary_frame()
print(predictions_summary_frame)
以下是输出的前几行:

绘制测试数据的预测计数与实际计数。
predicted_counts=predictions_summary_frame['mean']
actual_counts = y_test['BB_COUNT']
fig = plt.figure()
fig.suptitle('Predicted versus actual bicyclist counts on the Brooklyn bridge')
predicted, = plt.plot(X_test.index, predicted_counts, 'go-', label='Predicted counts')
actual, = plt.plot(X_test.index, actual_counts, 'ro-', label='Actual counts')
plt.legend(handles=[predicted, actual])
plt.show()
这是输出:
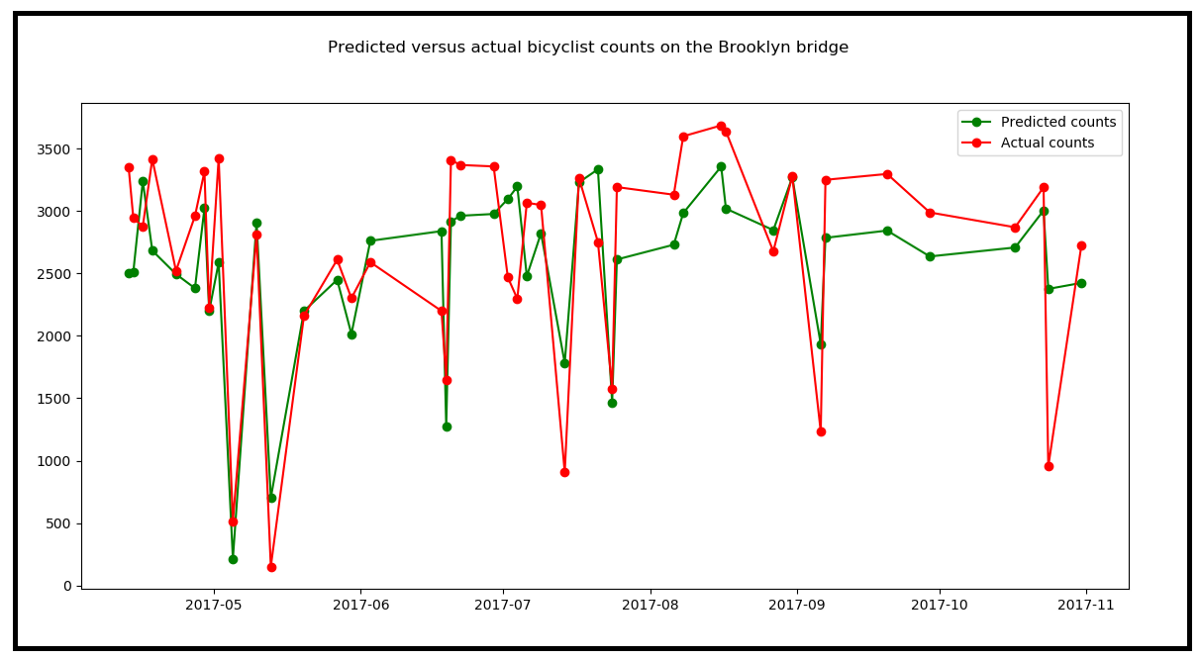
该模型似乎或多或少地跟踪了实际计数的趋势,尽管在许多情况下其预测与实际值相差甚远。
绘制实际计数与预测计数的关系图。
plt.clf()
fig = plt.figure()
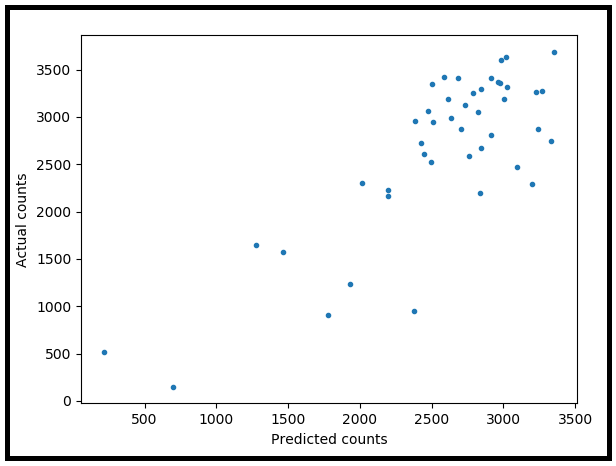
fig.suptitle('Scatter plot of Actual versus Predicted counts')
plt.scatter(x=predicted_counts, y=actual_counts, marker='.')
plt.xlabel('Predicted counts')
plt.ylabel('Actual counts')
plt.show()
8 泊松回归模型的拟合优度
泊松分布的期望值(即均值)和方差均为 λ。大多数现实世界的数据都违反了这个相当严格的条件。
泊松回归模型失败的一个常见原因是数据不满足泊松分布规定的均值 = 方差标准。
statsmodels GLMResults 类上的 summary() 方法显示了一些有用的拟合优度统计数据,可帮助评估泊松回归模型是否能够成功拟合训练数据。
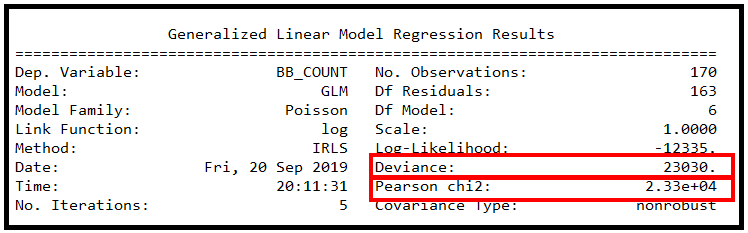
报告的偏差和皮尔逊卡方值非常大。考虑到这些值,几乎不可能实现良好的拟合。为了在某个置信水平(例如 95% (p=0.05))下定量确定拟合优度,在 χ2 表中查找 p=0.05 和残差自由度=163 的值。 (DF 残差 = 观察次数减去 DF 模型])。
将此卡方值与观察到的统计数据进行比较,在本例中为 GLMResults 中报告的偏差或皮尔逊卡方值。在 p=0.05 且 DF 残差 = 163 时,标准卡方表中的卡方值为 193.791,远小于报告的统计数据 23030 和 23300。
因此,根据此测试,泊松回归模型尽管展示了对测试数据集的“良好”视觉拟合,但与训练数据的拟合却相当差。
参考:
https://timeseriesreasoning.com/contents/poisson-regression-model/
https://omarfsosa.github.io/poisson_regression_in_python
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.PoissonRegressor.html
https://mengte.online/archives/12747
这篇关于python实现泊松回归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







