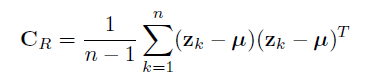本文主要是介绍协方差(covariance)和相关系数(correlation coefficient),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
相关系数和协方差实际上是相同的概念,都是用来描述两个随机变量之间的相似程度的。这篇文章将详细说明协方差和相关系数的相关知识。
首先声明,此篇的内容是来自"马同学高等数学"微信公众号的内容。
1、事物之间的关系
事物之间有两种关系,有关系和没关系。
1.1 、有关系
据专家表示,要买房的人越多(下图的城镇化率可以简单理解为进城买房的人数),房价就越高(数据来源):
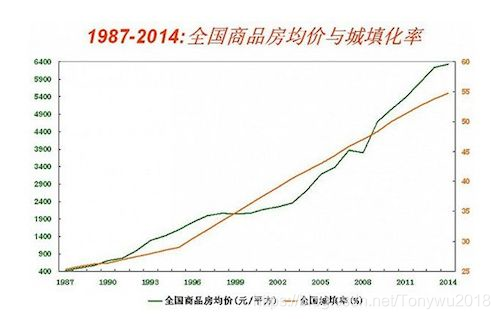
从上图可以看出,房价与进城买房的人数成正比,两者的关系是正相关。
城镇化除了推升城市房价之外,还有另外一个作用,降低出生率。城镇化和出生率之间的关系就是负相关:
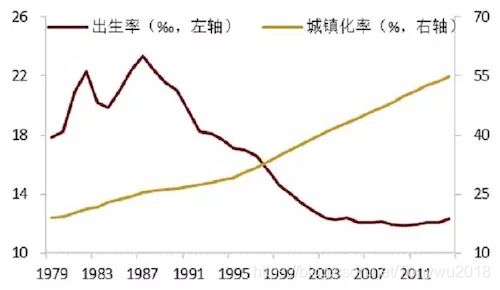
所以说,“城镇化是最好的避孕药”,不管在新加坡、日本、中国、美国都有这样的规律。城镇化一方面是推动买房人口的增加,一方面是出生人口的减少,那么未来房价会怎样?预测未来就是统计学家的重要工作。
1.2、没关系
比如说买彩票,跟是否求神拜佛,是否洗手这些事没有关系的。

协方差、相关系数就是尝试找出两个随机变量之间具有什么样的关系。
2、距离与关系
在线性代数里面是用距离来描述关系的。比如,几米的漫画《向左走,向右走》,讲述了一对都市男女,比邻而居:
却总是擦肩而过:

用句文艺的话来说就是,“距离那么近,相隔那么远”。
这里面就包含了两个数学中的距离:
-
“距离那么近”:欧式距离,也就是两点之间的直线距离
-
“相隔那么远”:余弦距离,也就是本文想说的,表示关系用的距离
2.1 欧式距离
欧式距离是我们接触最多的距离,实际上他就是直线距离。比如,和
之间的欧式距离就是下图中的许下:
欧式距离可以通过勾股定理,或者点积来计算:
![]()
2.2 余弦距离
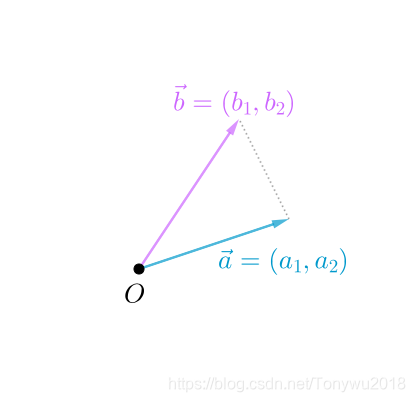
比如,向量和
的余弦距离就是下图中
角的余弦

根据线性代数的知识,余弦也可以通过点积和模长来计算:
![]()
2.3 通过余弦距离来计算关系
举一个在实际应用中,通过余弦距离来计算关系的例子。下面是某书评网站,用户对一些书籍进行了相应的评分:

第一个用户的信息用向量来表示,第二个用户的信息用向量
来表示,那么他们之间的相似性可以用余弦距离来表示:
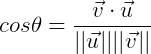
带入数据,结果保留到小数点后两位:
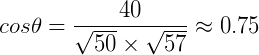
余弦最大即为1,所以两者之间应该是挺有关系的,我们可以考虑把第一个用户喜欢的书推荐给第二个用户,或者反之。以此类推,我们就可以做出如下表格,表明各个用户的相关性:
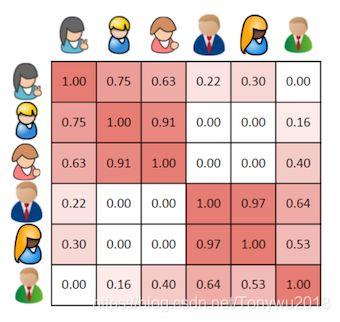
但是这有一个问题,比如第一个用户喜好假如是:,也就是说他对所有书籍的评分都是1.
第二个用户的喜好是:,也就是说他对所有书籍的评分都是5。这两个人的喜好不是很相同,但是:
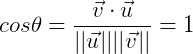
余弦距离表明两个人的喜好是完全相同的。
我们来改进一下:
-
5分,表示很喜欢,实际值为2
-
4分,表示喜欢,实际值为1
-
3分,表示中性态度,实际值为0
-
2分,表示讨厌,实际值为-1
-
1分,表示很讨厌,实际值为-2
-
不打分,默认实际值为0
因此,第一个用户喜好的实际值为:![]()
同样的,第二个用户的喜好的实际值为:![]()
余弦距离的结果为: 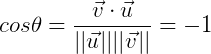
-1表示两人的喜好是相反的。-1,也就是相反的喜好不代表不相关,而是负相关。我们可以这么来看,比如我们知道第一个用户和第二个用户的余弦距离为-1,那么第一个用户喜欢的就不要推荐给第二个用户,第一个用户讨厌的可以推荐给第二个用户,所以实际两人是相关的,而且还非常相关。
3、协方差和相关系数
扯了这么多有的没的,我们该回到正题了。先假设有两个随机量 ,其均值分别为
。
由这两个随机量及其均值组成两个向量(可以这么认为,对于随机变量组成的向量,其均值才是原点): ![]() 好,准备好了,我们往下走。
好,准备好了,我们往下走。
3.1 、样本方差
对于 X ,其样本方差为:
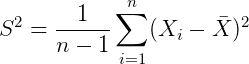
通过向量表示为: ![]() 方差看起来很像是欧式距离。
方差看起来很像是欧式距离。
3.2 、样本协方差
对于X,Y,其样本协方差为:

通过向量表示为: ![]() 协方差看起来很像点积。
协方差看起来很像点积。
其实协方差已经可以表示两个向量之间的关系了,但是会受到向量长度的影响,比如:

虽然两个向量的夹角相等,但是算出来的协方差,除了符号相同外,数值却相差较大,为了解决这个问题,我们把协方差归一化,也就是相关系数。
3.3、样本相关系数
对于 X,Y ,样本相关系数为: ![]() 其中
其中 为标准差。
通过向量表示为:
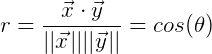
相关系数其实就是之前说的余弦距离,表示事物之间的相关性。对比之前关于网站书评的例子,容易知道:
-
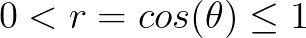 ,则正相关
,则正相关 -
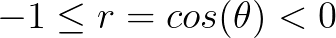 ,则负相关
,则负相关 -
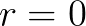 ,则不相关 .要说明的一点是,
,则不相关 .要说明的一点是, 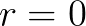 代表不相关,并不一定独立。这和线代的独立含义还是有所不同。
代表不相关,并不一定独立。这和线代的独立含义还是有所不同。
4、通过散点图来看待相关系数
之前是通过向量来解释了相关系数,不过随机变量 X,Y, 一般数值都很多,组成的向量都超过三维,这样就没有直观的几何意义了,所以我们一般用散点图来表示。比如说,我这里有一组身高、体重的数据:
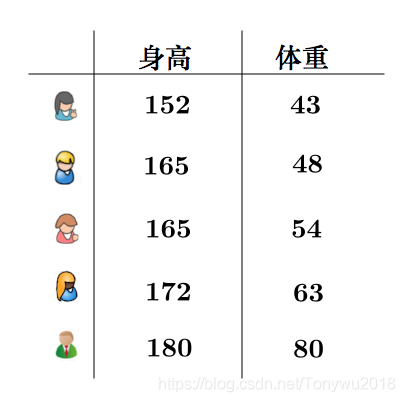
相关系数为:![]() 和我们直觉相符,体重和身高确实是有强烈的正相关关系。把(身高,体重)作为一个点,画成散点图:
和我们直觉相符,体重和身高确实是有强烈的正相关关系。把(身高,体重)作为一个点,画成散点图:
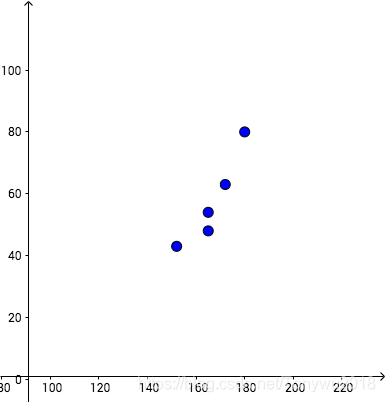
从散点图也可以看出,这些点并非随机,其实是有规律的,可以认为它们贴合在下面红色直线的周围:
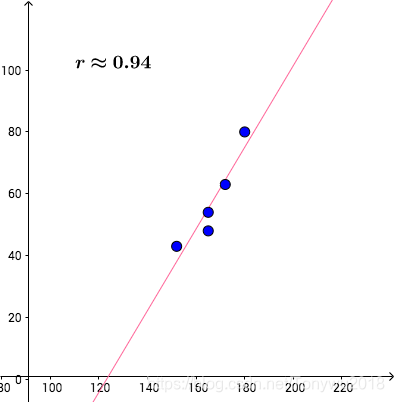
而下面这样的点才是散乱无章的,所以相关系数接近于零:
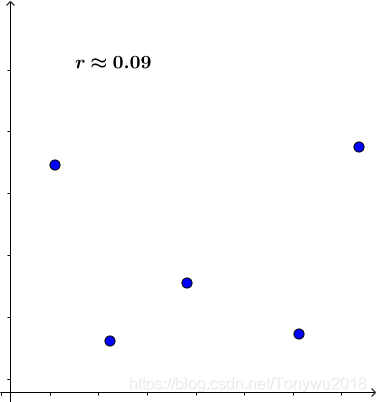
最后用维基百科给出的散点图来结束,该散点图给出了不同形态的点分布与相关系数之间的关系:

参考文献:
如何理解协方差、相关系数? https://mp.weixin.qq.com/s/oejfQS-705PI5DhmC4AAug
这篇关于协方差(covariance)和相关系数(correlation coefficient)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!