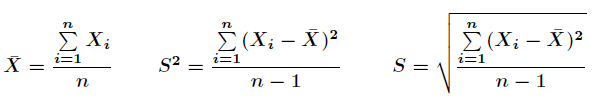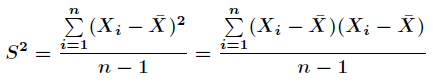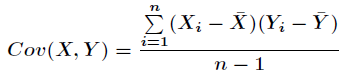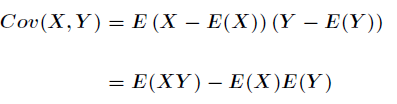本文主要是介绍协方差和协方差矩阵简要概述,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在统计学中,我们见过的最基本的三个概念是均值,方差,标准差。假定给定了n个样本的集合,那么公式如下
均值是描述样本的平均值,标准差描述的是样本集合的各个点到均值距离的平均,体现了样本的散步程度。而方
差仅仅是标准差的平方。
实际上,上述的方差是针对一维数据的情况进行统计描述。考虑这样一种情况:假设我们需要对两个集合的数据
进行分析,比如来看一个男孩子的猥琐程度与他受女孩子欢迎程度之间是否有联系。那么协方差就是用来度量这
两个随机变量关系的统计量。先把方差公式变形如下
那么仿照方差的定义,两个随机变量的协方差计算公式如下
如果协方差的值为负值,表示两者是负相关的,即男孩越猥琐,女孩越不喜欢。
如果协方差的值为正值,表示两者是正相关的,即男孩越猥琐,女孩越喜欢。
如果协方差的值为零,表示两者之间没有联系,即男孩猥不猥琐与女孩喜不喜欢没有关系。
协方差更为一般的表示如下
对于一个n维随机变量,两两计算协方差,可以得到协方差矩阵。
这篇关于协方差和协方差矩阵简要概述的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!