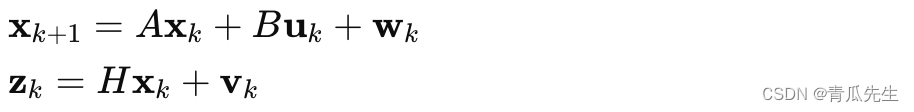卡尔曼滤波专题
无迹卡尔曼滤波算法(C语言代码)
无迹卡尔曼滤波(Unscented Kalman Filter, UKF)是一种非线性状态估计算法,它通过无迹变换来处理非线性系统,相比扩展卡尔曼滤波(EKF),UKF在处理非线性系统时更具鲁棒性。下面是一个简单的无迹卡尔曼滤波器的C语言实现示例。这个实现展示了如何定义UKF并进行状态估计。 #include <stdio.h>#include <math.h>#include <strin
MATLAB代码|中心差分卡尔曼滤波(CDKF)的滤波例程,无需下载,直接复制到MATLAB上面就能运行
文章目录 CDKF介绍代码运行结果各模块解析初始化系统模型设置CDKF循环绘图 另有关于EKF和CDKF的对比程序:EKF+CDKF两个滤波的MATLAB程序,估计三轴位置,带中文注释—— https://blog.csdn.net/callmeup/article/details/136610153。 CDKF介绍 中心差分卡尔曼滤波(Central Differe
卡尔曼滤波实现一阶马尔可夫形式的滤波|价格滤波|MATLAB代码|无需下载,复制后即可运行
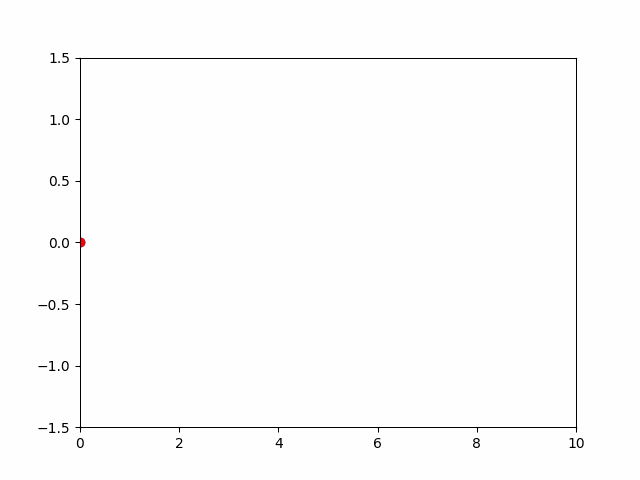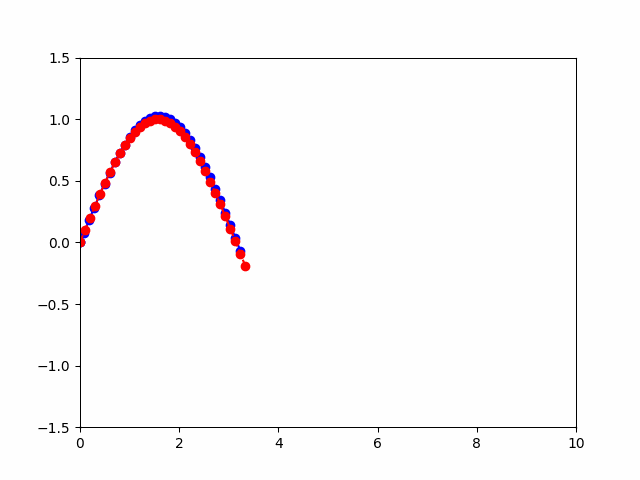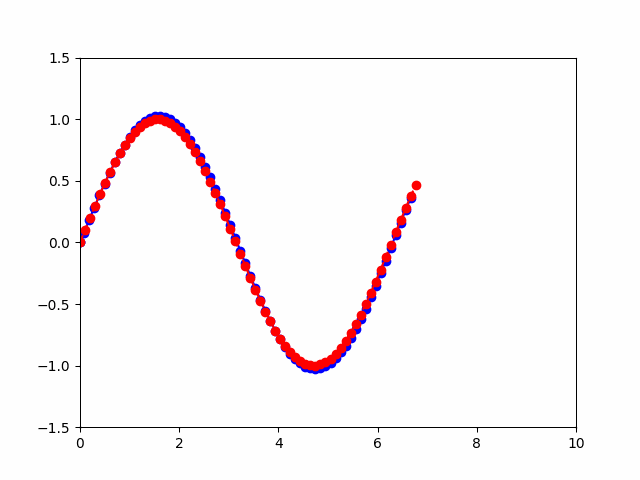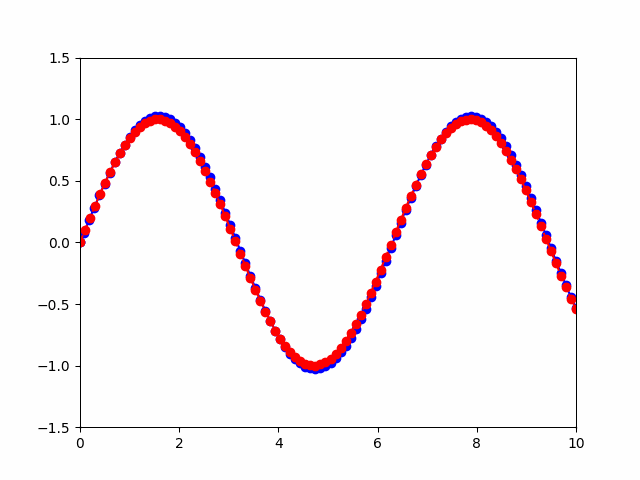
一节马尔可夫 一阶马尔可夫噪声是一种具有马尔可夫性质的随机过程。在这种噪声中,当前时刻的状态只与前一时刻的状态有关,与更早的状态无关。 一阶马尔可夫噪声可以用一个状态转移矩阵表示,矩阵的每个元素表示从一个状态转移到另一个状态的概率。 滤波模型 状态量的迭代模型如下: 观测量为X的第一维,所以观测方程也就是取X的第一维。 运行结果 应用背景为价格滤波,所以对比X真值和滤波值的第一维
卡尔曼滤波公式通俗理解
本文需要配合博客卡尔曼滤波详解进行理解 1.简单介绍 参考卡尔曼滤波详解 上面可简化理解为 2.主要过程 主要过程还是参考卡尔曼滤波详解 3.实例 这里以线性运动为例 3.1 前期定义状态和变量 3.1.1分析运动情况 已知线性运动上一状态和当前状态的关系,假设没有噪声干扰,为 { x ′ = x + v x Δ t y ′ = y + v y Δ t \begin{
【逐行注释】容积卡尔曼滤波的MATLAB例程(三维CKF),无需下载,可直接复制代码到MATLAB上运行
文章目录 CKF完整源代码与注释程序运行结果绘图部分误差的统计特性计算与输出部分 CKF CKF全称为容积卡尔曼滤波,相比于UKF(无迹卡尔曼滤波),拥有更合理的理论推导和鲁棒性,且在理论上比UKF的精度更高。 另有: 与EKF的对比程序:https://blog.csdn.net/callmeup/article/details/136147833 完整源代码与注释
卡尔曼滤波算法(c语言代码)
卡尔曼滤波器是一种用于估计动态系统状态的算法,常用于信号处理、控制系统、机器人和导航等领域。以下是一个简单的卡尔曼滤波器的 C 语言实现示例。这个示例展示了如何使用卡尔曼滤波器来估计一维系统的状态。 1. 卡尔曼滤波器算法概述 卡尔曼滤波器由两部分组成:预测和更新。基本的卡尔曼滤波器包括以下步骤: 预测步骤: 预测状态估计值。预测协方差矩阵。 更新步骤: 计算卡尔曼增益。更新状态估计值。更
【逐行注释】MATLAB下的UKF(无迹卡尔曼滤波),带丰富的中文注释,可直接复制到MATLAB上运行,无需下载
文章目录 程序组成部分完整代码运行结果主要模块解读:运动模型绘图部分误差统计特性输出 程序组成部分 由模型初始化、运动模型、UKF主体部分、绘图代码和输出部分组成: 完整代码 将下列代码复制粘贴到MATLAB里面,即可运行: % 三维状态量的UKF例程% 作者联系方式:微信matlabfilter(除前期达成一致外,付费咨询)% date: 2024-8-7/V
卡尔曼滤波器、扩展卡尔曼滤波器、无向卡尔曼滤波器的详细推导
这段时间做轴承故障诊断和预测的时候,需要一个针对已经获取了特征向量的工具来对轴承故障状态进行估计和预测。卡尔曼滤波器可以实现对过去、当前和未来目标位置的估计,所以想通过卡尔曼滤波器的设计思路找到一些灵感。虽然最后发现:卡尔曼滤波器中的状态量是有具体的物理含义的物理量,而表征轴承故障状态的量只是一种表征量。这两者之间存在着本质的差别,因为轴承的退化过程目前为止还不能建模。虽然如此,我还是想将卡尔曼滤
卡尔曼滤波详解:一维卡尔曼滤波实例解析(五个公式以及各个参数的意义)
一、引言 本文以rssi(接收信号强度)滤波为背景,结合卡尔曼的五个公式,设计 rssi 一维卡尔曼滤波器,用MATLAB语言实现一维卡尔曼滤波器,并附上代码和滤波结果图; 本文工分为以下几个部分: 1、引言 2、模型的系统方程和状态方程 3、卡尔曼滤波过程及五个基本公式 4、公式中每个参数详细注释 5、结合rssi滤波实例设计滤波器 6、MATLAB实现滤波器 二、模型的
风速预测 | 基于MATLAB的无迹卡尔曼滤波算法UKF、SVR-UKF、ANN-Kalman等时间序列风速预测模型
基本描述 基于MATLAB的无迹卡尔曼滤波算法UKF、SVR-UKF、ANN-Kalman等时间序列风速预测模型 模型步骤 时间序列风速预测模型基于MATLAB的无迹卡尔曼滤波算法(Unscented Kalman Filter, UKF)、SVR-UKF(Support Vector Regression - Unscented Kalman Filter)和ANN-Kalman(Arti
【数学和算法】扩展卡尔曼滤波器(六)
本文是观看B站视频【卡尔曼滤波器】6_扩展卡尔曼滤波器_Extended Kalman Filter所做的截图和笔记。 前面讲的都是线性系统,他们可以用卡尔曼滤波器进行预测。 对于非线性系统,可以将非线性系统线性化,就需要用到扩展卡尔曼滤波器。 线性化:泰勒级数 视频 对于泰勒公式的讲解,请跳转参考这篇博客:泰勒公式_线性化。 对于一维度的非线性系统进行线性化,就是泰勒一阶展开,对于高维度
【数学和算法】初识卡尔曼滤波器(四)
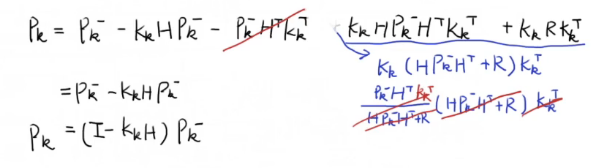
本文是观看B站视频教程【卡尔曼滤波器】4_误差协方差矩阵数学推导_卡尔曼滤波器的五个公式 所做的截图和笔记。 先列出前面几篇博客得到的公式: 下面是利用上图公式推导 P k − \displaystyle\color{blue}P_k^- Pk−的过程: 先写出接下来的计算会用到的东西: 上一次的真实值减去上一次的估计值: 由于 W k − 1 \displaystyle\color{
【数学和算法】初识卡尔曼滤波器(三)
本文是观看B站视频教程所做的截图和笔记。 疑问: 1.观测矩阵H是单位矩阵吗?如果是的话,那么卡尔曼增益的两种写法都合理。那么他的作用是对 X k X_k Xk向量进行变换为 Z k Z_k Zk向量的各个维度对应吗? 答:观测矩阵H可以是单位矩阵,但是也可以不是单位矩阵。他把状态量变换成和观测量对应的特征值。2.卡尔曼增益 K k K_k Kk是矩阵还是实数? 答:卡尔曼增益 K k
卡尔曼滤波源码注释和调用示例
卡尔曼滤波源码注释和调用示例 flyfish Python版本代码地址 C++版代码地址 主要用于分析代码,增加了中文注释 import numpy as npimport scipy.linalg"""0.95分位数的卡方分布表,N自由度(包含N=1到9的值)。取自MATLAB/Octave的chi2inv函数,用作Mahalanobis门限。"""chi2inv95 = {1
从最小二乘法的角度来理解卡尔曼滤波(1)
从最小二乘法的角度来理解卡尔曼滤波(1) flyfish 假设你有一堆数据点,比如在一个二维平面上有很多点。你想找到一条直线,能够尽可能接近这些点。这条直线可以用一个方程来表示:y = mx + b,其中 m 是斜率,b 是截距。 但是这些数据点通常不会完美地在这条直线上,而是散布在它的周围。每个点与这条直线之间的距离称为误差(残差)。为了找到最佳的直线,我们希望所有这些误差的平方和最小。为
【数据融合】基于卡尔曼滤波实现GPS-IMU数据融合附matlab代码
下面是一个简单的示例代码,用于基于卡尔曼滤波实现GPS-IMU数据融合的MATLAB实现: matlab % 初始化卡尔曼滤波器参数 dt = 0.1; % 时间步长 A = [1 dt; 0 1]; % 状态转移矩阵 B = [0.5*dt^2; dt]; % 输入控制矩阵 H = [1 0]; % 观测矩阵 Q = eye(2); % 状态噪声协方差矩阵 R_gps = 0.1; % GP
DeepSORT(目标跟踪算法)卡尔曼滤波中的贝叶斯定理
DeepSORT(目标跟踪算法)卡尔曼滤波中的贝叶斯定理 flyfish 从例子中介绍名词 假设我们有一个袋子,里面有5个红球和3个蓝球。我们从袋子里随机抽取一个球。 概率 (Probability) 我们想计算从袋子里抽到红球的概率 P ( R ) P(R) P(R)。 红球的数量是5,球的总数量是8,所以抽到红球的概率是: P ( R ) = 5 8 P(R) = \frac{
DeepSORT(目标跟踪算法) 卡尔曼滤波的完整流程
DeepSORT(目标跟踪算法) 卡尔曼滤波的完整流程 flyfish DeepSORT(目标跟踪算法)中的状态向量与状态转移矩阵 DeepSORT(目标跟踪算法)中卡尔曼滤波器中的更新 DeepSORT(目标跟踪算法)中卡尔曼增益的理解 DeepSORT(目标跟踪算法)中的卡尔曼滤波 - 看了就会的状态转移矩阵 DeepSORT(目标跟踪算法)中的初始化卡尔曼滤波器的状态向量和协方差
DeepSORT(目标跟踪算法) 卡尔曼滤波 状态向量是如何映射到观测向量(测量向量)的即观测矩阵的构建方式
DeepSORT(目标跟踪算法) 卡尔曼滤波 状态向量是如何映射到观测向量(测量向量)的即观测矩阵的构建方式 flyfish 测量向量和观测变量在卡尔曼滤波的上下文中通常是同一个意思。它们都指的是从系统中直接获得的数据,这些数据用于更新系统的状态估计。可以是从传感器或测量设备直接获得的数据。这些数据反映了系统在某一时刻的状态或者实际观测到的值,但通常带有噪声。 状态向量映射到观测向量的过程通过
DeepSORT(目标跟踪算法)中的初始化卡尔曼滤波器的状态向量和协方差矩阵
DeepSORT(目标跟踪算法)中的初始化卡尔曼滤波器的状态向量和协方差矩阵 flyfish 如果看了下面遇到了状态转移矩阵,可以先看 DeepSORT(目标跟踪算法)中的卡尔曼滤波 - 看了就会的状态转移矩阵 ,这里做了非常详细的描述 import numpy as npnp.set_printoptions(suppress=True)class KalmanFilter(object)
DeepSORT(目标跟踪算法)中卡尔曼滤波器中的预测
DeepSORT(目标跟踪算法)中卡尔曼滤波器中的预测 flyfish 先略再详,先简洁的说,再细说。 卡尔曼滤波器的预测步骤主要有两个目标: 预测下一时刻的状态向量:根据当前状态和运动模型,预测对象在下一时刻的位置和速度。更新协方差矩阵:根据运动模型和过程噪声,更新预测的状态不确定性。 两个重要的点 运动模型:由状态转移矩阵 F \mathbf{F} F 描述,在代码中是 self.
卡尔曼滤波(Kalman Filtering)详细解读
🧑🎓 个人主页:《爱蹦跶的大A阿》 🔥当前正在更新专栏:《VUE》 、《JavaScript保姆级教程》、《krpano》、《krpano中文文档》 ✨ 前言 卡尔曼滤波(Kalman Filtering)是一种用于估计动态系统状态的递推算法,被广泛应用于控制系统、信号处理、经济学、导航和机器人学等领域。它是由瑞典数学家鲁道夫·卡尔曼(Rudolf E. Kalm
C语言 | 基于MPU6050的卡尔曼滤波算法(代码类)
博主github:https://github.com/MichaelBeechan 博主CSDN:https://blog.csdn.net/u011344545 //float gyro_m:陀螺仪测得的量(角速度)//float incAngle:加计测得的角度值#define dt 0.0015//卡尔曼滤波采样频率#define R_angle
C语言 | 卡尔曼滤波器算法1——应用介绍(Matlab simulink)
github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ============================================================ 其他相关卡尔曼滤波博客: 单片机开发 | 基于51单片机实现MPU6050的卡尔曼滤波算法(代码类) 单片机开发 |