本文主要是介绍【数学和算法】初识卡尔曼滤波器(三),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文是观看B站视频教程所做的截图和笔记。
疑问:
- 1.观测矩阵
H是单位矩阵吗?如果是的话,那么卡尔曼增益的两种写法都合理。那么他的作用是对 X k X_k Xk向量进行变换为 Z k Z_k Zk向量的各个维度对应吗?
答:观测矩阵H可以是单位矩阵,但是也可以不是单位矩阵。他把状态量变换成和观测量对应的特征值。 - 2.卡尔曼增益 K k K_k Kk是矩阵还是实数?
答:卡尔曼增益 K k K_k Kk是矩阵。当测量噪声的协方差矩阵R特别小时,卡尔曼增益 K k K_k Kk趋近于H的逆H − 1 H^{-1} H−1。所以卡尔曼增益 K k K_k Kk和观测矩阵H行和列维度一样。
无论是算出来的结果,还是测量出来的结果,都不具备噪声的影响。如果你可以完整建模噪声的话,就不存在卡尔曼滤波器了,也就不存在观测器的作用了,因为你可以得到这个结果。
因为存在噪声,所以这两个结果都是不准确的,此时,卡尔曼滤波器的作用就体现出来了。
且看卡尔曼滤波器如何通过2个不太准确的结果得出一个准确结果:
注意区分先验和逆的符号表示,对于Xk和Pk右上角跟一个-的,就是先验,不跟-就是后验.对于H后面跟一个-就表示逆。有的右上角符号是-T,表示的是先验的转置。
文中的下标k表示k时刻。
我们一般会假设过程噪声和测量噪声都符合正态分布。
下面这张截图摘自卡尔曼滤波五个公式推导,每个变量是什么都写的比较清楚。


从下面开始都是B站的截图: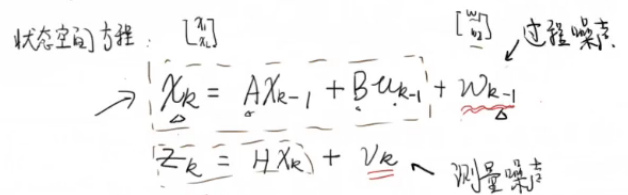
去掉两个噪声,如下

上面的(1)式,由于去掉了过程噪声那一项,所以是不完整的,头顶加上^表示是估计值,由于我们没对他们做任何处理,右上角加上-表示先验,合起来就叫先验估计。
后 验 X k ^ = 先 验 X k − ^ + G ∗ ( 测 量 值 X k m e a s u r e d − 先 验 X k − ^ ) \displaystyle\color{blue}后验\hat{X_k} = 先验\hat{X_k^-} + G*(测量值X_k{measured} - 先验\hat{X_k^-}) 后验Xk^=先验Xk−^+G∗(测量值Xkmeasured−先验Xk−^)
G G G 是卡尔曼增益,而教科书中给出的卡尔曼增益是 K k K_k Kk,二者之间的关系有:
G = K k ∗ H \displaystyle\color{blue}G = K_k * H G=Kk∗H。
接下来我们需要量化误差, e k = X k − X k ^ \displaystyle\color{blue}e_k = X_k - \hat{X_k} ek=Xk−Xk^,误差也满足正态分布。

注意:
- e k = X k − X k ^ \displaystyle\color{blue}e_k = X_k - \hat{X_k} ek=Xk−Xk^,其中 X k {X_k} Xk是第
k时刻的实际值, X k ^ \hat{X_k} Xk^是第k时刻的后验估计值。 - 先验误差 e k − = X k − X k − ^ \displaystyle\color{blue}e_k^- = X_k - \hat{X_k^-} ek−=Xk−Xk−^ ,其中 X k X_k Xk是第
k时刻的实际值, X k − ^ \hat{X_k^-} Xk−^是第k时刻的先验估计值。
我们知道,方差越小,误差就越小,也就越接近期望值。
为了使得方差最小,我们就是要使得协方差矩阵的迹最小,如下:

对于 e k e_k ek的协方差矩阵P,把 e k e_k ek代入下面P中得到:
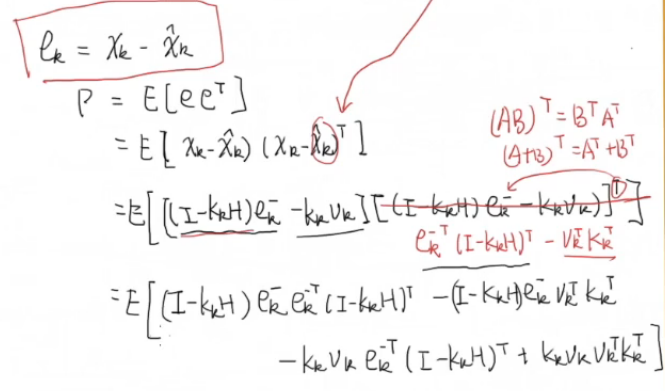
上面的P就是 P k P_k Pk,含义见下面: 由于上面的期望
由于上面的期望E中式子是线性的,所以可以随他们分别求期望:
由于 e k e_k ek和测量噪声v都满足正态分布,所以他们的期望都为0,所以上面的有些式子可以直接划掉。
如果两个不同的变量A和B是独立同分布的,那么期望E(AB)=E(A)*E(B)。
上面的式子化简后得到:

前面的所有式子都是在求P, P就是Pk:
下一篇博客会讲到怎么求 P k P_k Pk的先验 P k − P_k^- Pk−,即上式的等号右边第一项。
由于前面的式子中的第二个和第三个有以下转置关系:

方阵有个定理是,矩阵A和矩阵A的逆 A − 1 A^{-1} A−1,他们的的迹相等。所以上面第二三个式子的迹相等。
推导了这么多,别忘了我们开始的目标是,为了使得方差最小,我们就是要使得协方差矩阵的迹最小:

要求协方差的迹最小,就是迹对 K k K_k Kk求导==0,
该方法证明在矩阵的迹可以看到。


最后得到:
P k P_k Pk是协方差矩阵,又因为协方差矩阵的转置等于他自己,化简得到:
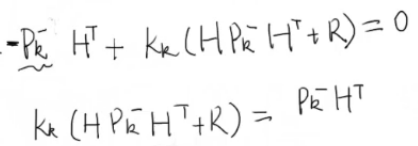
最终求得 K k K_k Kk:
该公式就是卡尔曼滤波器中最核心的公式。
(下一篇博客会讲到分子的 P k − P_k^- Pk−即 P k P_k Pk的先验是怎么得到的。)
得到了卡尔曼增益 K k K_k Kk,我们再回过头来分析:

当测量噪声的协方差矩阵R特别大时,卡尔曼增益 K k K_k Kk趋近于0,此时估计值就等于先验估计值,我们更愿意相信计算出来的结果。
当测量噪声的协方差矩阵R特别小时,卡尔曼增益 K k K_k Kk趋近于H逆 H − 1 H^{-1} H−1,此时估计值就等于 测 量 值 ∗ H − 1 \displaystyle\color{blue}测量值*H^{-1} 测量值∗H−1 ,我们更愿意相信测量出来的结果。

------------------------------------------------------------------
w是过程噪声(即过程噪声是n维向量,它的每一维度都表示噪声的一个特征),P(w)是
过程噪声的概率分布,0是过程噪声的期望,Q是过程噪声的协方差矩阵。
我们一般会假设过程噪声和测量噪声都符合正态分布。
下面是以过程噪声是2维向量为例来推导公式:

由于方差和期望有以下关系:
V a r ( x ) = E ( x 2 ) − E 2 ( x ) \displaystyle\color{blue}Var(x) = E(x^2) - E^2(x) Var(x)=E(x2)−E2(x)
对于正态分布,他的期望 E ( x ) = 0 \displaystyle\color{blue}E(x) = 0 E(x)=0所以 E 2 ( x ) = 0 \displaystyle\color{blue}E^2(x) = 0 E2(x)=0
所以方差就等于 V a r ( x ) = E ( x 2 ) \displaystyle\color{blue}Var(x) = E(x^2) Var(x)=E(x2)
所以可以得到上面的协方差矩阵。
上面的协方差矩阵的书写方式会造成误解,因为X和Y协方差 并不等于 X的标准差乘以Y的标准差,而且可正可负,在这里是表示二者之间的协方差,并不是二者标准差相乘。这篇博客的最后介绍了相关系数:

这篇关于【数学和算法】初识卡尔曼滤波器(三)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









