本文主要是介绍【数学和算法】初识卡尔曼滤波器(四),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文是观看B站视频教程【卡尔曼滤波器】4_误差协方差矩阵数学推导_卡尔曼滤波器的五个公式 所做的截图和笔记。
先列出前面几篇博客得到的公式:

下面是利用上图公式推导 P k − \displaystyle\color{blue}P_k^- Pk−的过程:

先写出接下来的计算会用到的东西:
上一次的真实值减去上一次的估计值:
由于 W k − 1 \displaystyle\color{blue}W_{k-1} Wk−1是作用在 X k \displaystyle\color{blue}X_k Xk上的,所以 e k − 1 \displaystyle\color{blue}e_{k-1} ek−1和 W k − 1 \displaystyle\color{blue}W_{k-1} Wk−1是相互独立的。所以他们的期望之间关系右: E ( A B ) = E ( A ) ∗ E ( B ) \displaystyle\color{blue}E(AB) = E(A)*E(B) E(AB)=E(A)∗E(B)
又因为 e k − 1 \displaystyle\color{blue}e_{k-1} ek−1和 W k − 1 \displaystyle\color{blue}W_{k-1} Wk−1都是服从正态分布,所以期望为0,
E ( e k − 1 ) = 0 \displaystyle\color{blue}E(e_{k-1})=0 E(ek−1)=0 E ( W k − 1 ) = 0 \displaystyle\color{blue}E(W_{k-1})=0 E(Wk−1)=0

所以可以得到: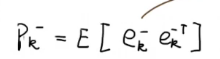

上面的Q是过程噪声w的协方差矩阵。
最终,我们就得到了卡尔曼滤波器的五个公式:

从(2)式子看出,先验误差协方差矩阵 P k − \displaystyle\color{blue}P_k^- Pk−依赖上一次的误差协方差 P k − 1 \displaystyle\color{blue}P_{k-1} Pk−1,所以我们需要在得到后验估计值 X k \displaystyle\color{blue}X_k Xk以后,更新本次的 P k \displaystyle\color{blue}P_k Pk(即公式5),以便下一时刻计算(2)式的先验误差协方差时可以使用它。
其中,公式5的推导过程如下: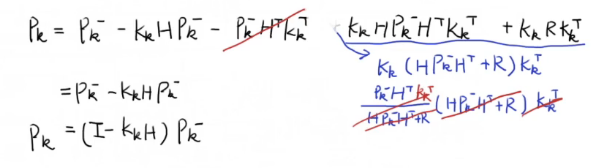
这篇关于【数学和算法】初识卡尔曼滤波器(四)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









