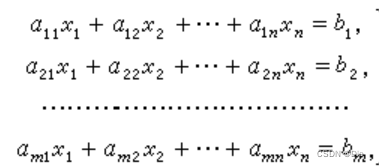高斯消专题
HDU 5833 高斯消元
n个数,任选>=1个数相乘,使得乘积是完全平方数。 其实就是开关,控制灯泡。 数 ----第i个质因子p的个数%2 = {1 , 0} == 开关----第i个灯泡 = {开 , 关} 最后使得所有灯泡都是灭着的方案数 = 2^自由变元个数 全部关着的情况 == 一个数也不选 应省去 import java.io.BufferedReader;
hiho一下第56周 高斯消元
小Ho:<吧唧><吧唧><吧唧> 小Hi:小Ho,你还吃呢。想好了么? 小Ho:肿抢着呢(正想着呢)...<吞咽>...我记得这个问题上课有提到过,应该是一元一次方程组吧。 我们把每一件商品的价格看作是x[1]..x[n],第i个组合中第j件商品数量记为a[i][j],其价格记作y[i],则可以列出方程式: a[1][1] * x[1] + a[1][2] * x[2] + ... +
poj 1222 EXTENDED LIGHTS OUT (高斯消元解异或方程组 开关问题)
近距离观摩今天北京站的比赛,向志愿者学姐要了一份题目,看了看H题; 因为数据被弱化,瞬间就想到了背包; 就先研究下标准解法——异或方程组; 下面为转载文: 题意:有一个5*6的矩阵,每个位置都表示按钮和灯,1表示亮,0表示灭。每当按下一个位置的按钮,它和它周围灯的状态全部翻转,问在这样的一个方阵中按下哪些按钮可以把整个方阵都变成灭的,这时1表示按了,0表示没按。 以下
poj1681 高斯消元+dfs枚举
wa N多次后,终于把高斯消元的模板给弄出来了,并且精简了许多。 用dfs枚举变元比二进制枚举变元简单多了。 (也终于明白 变元代表只得解的个数。) 上模板。 #include <iostream>#include <algorithm>using namespace std;int a[400][400];int ans[400],x[400];//ans[]用于记录哪几种
poj1222 枚举 和 高斯消元
接触开关问题,最先的方法是枚举。然后接触到了更加高深的高斯消元。 高斯消元的思想:把一个全部熄灭的矩阵经过一系列开关后得到初始的状态。 具体分析可参照 http://blog.csdn.net/shiren_Bod/article/details/5766907 下面附上的代码付注释: #include <iostream>using namespace std;int map[3
AcWing算法基础课笔记——高斯消元
高斯消元 用来求解方程组 a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 … a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n = b_1\\ a_
【C++】高斯消元算法
矩阵初等行变换法则 任一行可以与另一行进行加减。任一行可以乘或除以一个非零常数(除其实就是乘一个倒数)。任两行可以交换位置。 线性方程组 形如 a 1 , 1 x 1 + a 1 , 2 x 2 + ⋯ + a 1 , n x n = b 1 a 2 , 1 x 1 + a 2 , 2 x 2 + ⋯ + a 2 , n x n = b n ⋮ a n , 1 x 1 + a n , 2
To xor or not to xor 高斯消元求异或
【题目】 给你n个long long范围内的整数,你可以选取1个或多个数进行异或操作,使得结果最大,求最大的结果。 【题目分析】 真是一道好题,不是真正理解高斯消元是无法做这题的。 题意:给你n个数,可以选择任意个数异或,但是要使得最后的异或值最大。 我们把每个数用二进制表示,要使得最后的异或值最大,就是要让高位尽量为1,高位能不能为1就必须用高斯消元判断了。 1. 根据数的二进制表示,建立
UVA 1564 - Widget Factory(高斯消元)
UVA 1564 - Widget Factory 题目链接 题意:n种零件, 给定m个制作时间,每段时间制作k个零件,每种零件有一个制作时间,每段时间用Mon到Sun表示,求每个零件的制作时间,还要判断一下多解和无解的情况 思路:对于每段时间列出一个方程,这样一共列出m个方程解n个变元,利用高斯消元去求解,注意每个方程都是MOD 7的,所以在高斯消元过程中遇到除法要求该数字%7的逆
UVA 1563 - SETI (高斯消元+逆元)
UVA 1563 - SETI 题目链接 题意:根据题目那个式子,构造一个序列,能生成相应字符串 思路:根据式子能构造出n个方程,一共解n个未知量,利用高斯消元去解,中间过程有取摸过程,所以遇到除法的时候要使用逆元去搞 代码: #include <cstdio>#include <cstring>#include <algorithm>using namespace
UVA 1397 - The Teacher's Side of Math(高斯消元)
UVA 1397 - The Teacher's Side of Math 题目链接 题意:给定一个x=a1/m+b1/n,求原方程组 思路:由于m*n最多20,所有最高项只有20,然后可以把每个此项拆分,之后得到n种不同无理数,每一项为0,就可以设系数为变元,构造方程进行高斯消元 一开始用longlong爆了,换成分数写法也爆了,又不想改高精度,最后是机智的用了double型过
UVA 10808 - Rational Resistors(高斯消元+并查集+分数+基尔霍夫定律)
UVA 10808 - Rational Resistors 题意:给定一些结点,有一些电阻,电阻分布在边上,给定一个电路图,每次询问两点,求这两点间的等效电阻 思路:根据基尔霍夫定律,任意一点的电流向量为0,这样就能设每个结点的电势,列出方程,利用高斯消元求解,对于无解的情况,肯定是两点不能连通,这个可以利用并查集判断。 此外这题有个很坑的
UVA 1358 - Generator(dp+高斯消元+KMP)
UVA 1358 - Generator 题目链接 题意:有m种字符(从'A'开始往后数的大写字母),现在有一个字符串,长度不超过12,现在每次随机生成一个字母,要求能产生该字符串的期望长度 思路:dp[i]表示产生长度i的期望长度,那么每次产生一个字符,对应m种转移,每种转移的概率为1/m,转移后的长度可以利用KMP的next数组去快速获得,然后由于转移可能形成环的情况,所以无法直
HDU 3949 XOR(高斯消元搞基)
HDU 3949 XOR 题目链接 题意:给定一些数字,问任取几个异或值第k大的 思路:高斯消元搞基,然后从低位外高位去推算 代码: #include <cstdio>#include <cstring>#include <algorithm>using namespace std;typedef long long ll;const int N = 10005;
算法课程笔记——高斯消元
算法课程笔记——高斯消元 先乘后除,精度 #include<bist/stdc++.h>usingnamespacestd; #definemaxn 2800intn,m,x,ans; bitset<N>a[N]; voidgauss(){ intcnt=0; for(inti=1;i<=n;i++){ in
分别用高斯消元法和列主元消去法求解,(自制)表格比较两种算法的结果与精度,分析实验出现的问题,并总结解决办法。
以下是一个使用高斯消元法和列主元消去法求解线性方程组的示例: 假设我们要解决以下线性方程组: 4x + 2y + z = 8 -2x + y - 3z = -11 3x - 2y + 4z = 10 首先,我们可以将该线性方程组表示为增广矩阵的形式: [4 2 1 | 8] [-2 1 -3 | -11] [3 -2 4 | 10] 使用高斯消元法,我们可以进行以下操作: 将第一个方程
数论常用内容——高斯消元
高斯消元法 数学上,高斯消元法,是线性代数中的一个算法,可用来为线性方程组求解 高斯消元法求解线性方程组时,首先需要根据方程,列出增广矩阵。然后再利用初等行变换把增广矩阵转换为行阶梯阵,然后回代求出方程的解 高斯消元法的应用 1、找出可逆矩阵的逆矩阵 设A为一个N*N的可逆矩阵,将一个N*N单位矩阵I放在A的右边,形成一个N*2N的分块矩阵 B = [A,I] 。经过高斯消元法的计算程
XOR和路径 (HYSBZ - 2337 ,高斯消元解后效性 DP)
一.题目链接: HYSBZ-2337 二.题目大意: 给一张无向边权图,在每个节点都会等概率地选择一条边,求 1 ~ n 路径的权值异或和的期望值. 三.分析: 由于是异或,不妨按答案的二进制位逐位考虑. 假设当前考虑第 i 位 设 dp[u] 表示 u ~ n 路径的权值异或和二进制第 i 位的期望值. 设 v 是与顶点 u 相关联的顶点集合,de[u] 表示 u 的度, wi(
高斯消元 POJ 1222 POJ 1681(枚举自由变元)POJ 1753(两次高斯消元) POJ 1830 HDU 5833 (高斯消元,素数分解)POJ 3158 (集合压缩枚举自由变元)
高斯消元 POJ 1222 POJ 1681(枚举自由变元)POJ 1753(两次高斯消元) POJ 1830 HDU 5833 (高斯消元,素数分解)POJ 3158 (集合压缩枚举自由变元) POJ 2947(非01矩阵,求同模方程组的解) http://www.cppblog.com/menjitianya/archive/2014/06/08/207226.html ht
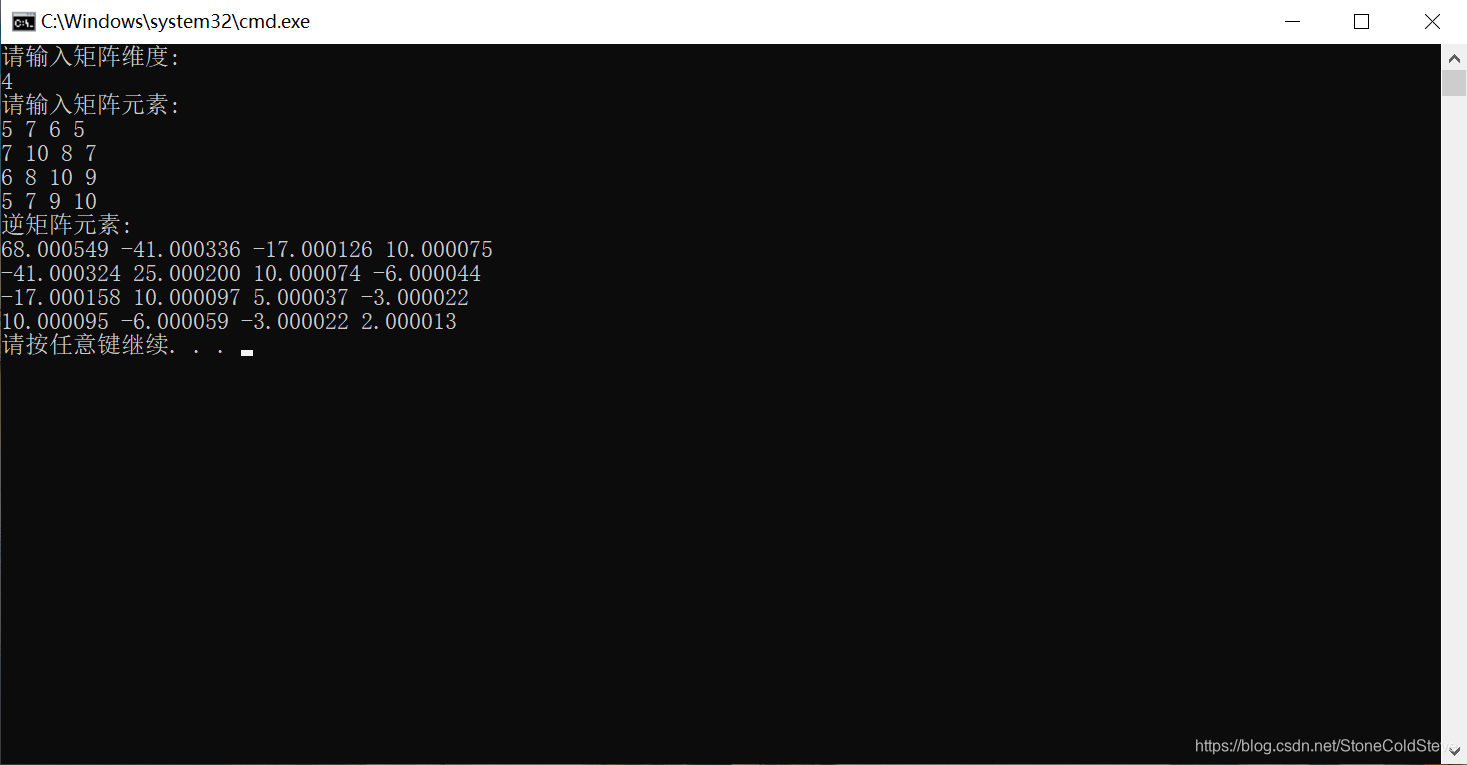
高斯消元法求矩阵的逆矩阵C语言实现
一 原理 在大学的线性代数课程中我们学习到了,想求一个 n n n维方阵的逆矩阵(如果存在的话),一种可行的方法是将其与一个对应维度的单位矩阵进行列的拼接,然后对所拼接的矩阵只进行初等的行变换并且当左侧的矩阵变换成为 n n n维的单位矩阵时,右侧的矩阵则为待求的逆矩阵,见式(1-1-1),其中矩阵 A A A是一个 n n n阶的方阵. 二 C语言实现 #include<stdio
acwing数学知识(三) 高斯消元 求组合数
1.高斯消元 描述:解一个包含n个方程n个未知数的线性方程组 算法流程:对每一列的系数进行如下操作 1.找到一列中系数绝对值最大的一条方程(不考虑已经移动过的方程) 2.将其移到最上方(同样不考虑移动过的方程) 3.将该系数变为1 4.将下面的方程同一列的系数消为0 5.得到一个倒三角形方程组,即可求出解 得出三种情况: ①完美在倒三角i选哪个 唯一解 ②0 = 非0 无解 ③0 = 0 无
AcWing.883.高斯消元解线性方程组
输入一个包含 n 个方程 n 个未知数的线性方程组。 方程组中的系数为实数。 求解这个方程组。 下图为一个包含 m 个方程 n 个未知数的线性方程组示例: 输入格式 第一行包含整数 n n n。 接下来 n n n 行,每行包含 n + 1 n+1 n+1 个实数,表示一个方程的 n n n 个系数以及等号右侧的常数。 输出格式 如果给定线性方程组存在唯一解,则输出共 n n



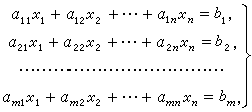

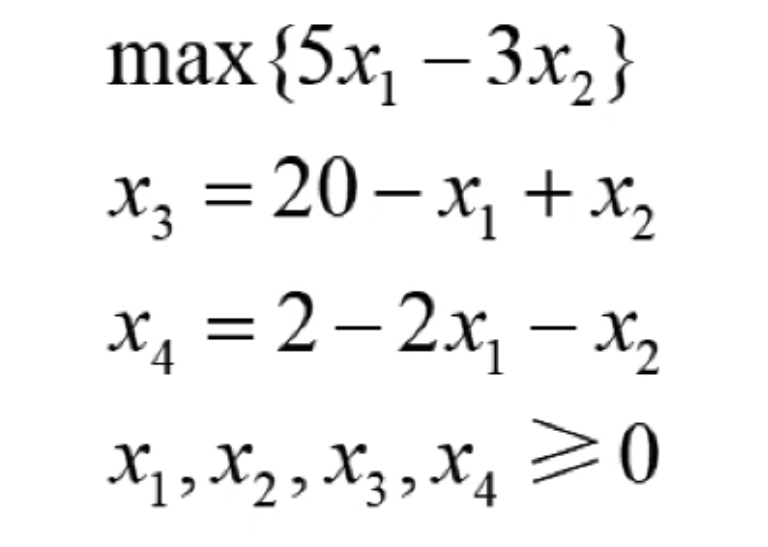
![[数学]高斯消元](https://img-blog.csdnimg.cn/direct/be179525c34c48c0832beb4aa4b0dc68.png)