高斯消元法求矩阵的逆矩阵C语言实现

本文主要是介绍高斯消元法求矩阵的逆矩阵C语言实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一 原理

​ 在大学的线性代数课程中我们学习到了,想求一个$n$维方阵的逆矩阵(如果存在的话),一种可行的方法是将其与一个对应维度的单位矩阵进行列的拼接,然后对所拼接的矩阵只进行初等的行变换并且当左侧的矩阵变换成为$n$维的单位矩阵时,右侧的矩阵则为待求的逆矩阵,见式(1-1-1),其中矩阵$A$是一个$n$阶的方阵.

---

二 C语言实现

#include<stdio.h>
#include<stdlib.h>
float **Matrix_Inv(float **array1, int n);
float Matrix_Det(float **array, int n);
int Matrix_Free(float **tmp, int m, int n);
void swap(float *src, float *dst, int n);
void Vector_Sub(float *src, float *dst, float value, int n);
int main(void)
{int n;printf("请输入矩阵维度:\n");scanf("%d", &n);float **array = (float **)malloc(n * sizeof(float *));if (array == NULL){printf("error :申请数组内存空间失败\n");return -1;}for (int i = 0; i < n; i++){array[i] = (float *)malloc(n * sizeof(float));if (array[i] == NULL){printf("error :申请数组子内存空间失败\n");return -1;}}printf("请输入矩阵元素:\n");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){scanf("%f", &array[i][j]);}}float **Result = Matrix_Inv(array, n);printf("逆矩阵元素:\n");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){printf("%f ", Result[i][j]);}printf("\n");}Matrix_Free(Result, n, n);return 0;
}
float **Matrix_Inv(float **array1, int n)
{int i, flag_det, flag_zero, j;flag_det = 0;flag_zero = 0;float **array = (float **)malloc(n * sizeof(float*));float **result = (float **)malloc(n * sizeof(float*));float **array1_temp = (float **)malloc(n * sizeof(float*));if (array == NULL){printf("error in Matrix_Inv:申请空间失败\n");return NULL;}for (i = 0; i < n; i++){array[i] = (float *)malloc(2 * n * sizeof(float));array1_temp[i] = (float *)malloc(n * sizeof(float));result[i] = (float *)malloc(n * sizeof(float));if (array[i] == NULL){printf("error in Matrix_Inv:申请子空间失败\n");return NULL;}}//copyfor (i = 0; i < n; i++){for (j = 0; j < n; j++){array1_temp[i][j] = array1[i][j];}}for (i = 0; i < n; i++){for (j = n; j < 2 * n; j++){if (i + n == j){array[i][j] = 1;}else{array[i][j] = 0;}}for (j = 0; j < n; j++){array[i][j] = array1[i][j];}}float temp = Matrix_Det(array1, n);if (temp == 0){printf("error in Matrix_Inv: 矩阵不可逆\n");return NULL;}else{for (i = 0; i < n - 1; i++){for (j = i; j < n; j++){if (array[j][i] != 0){if (j == i){break;}else{swap(array[i], array[j], n);flag_det++;break;}}else{flag_zero++;if (flag_zero == n - i){return 0;}}}flag_zero = 0;for (j = i + 1; j < n; j++){if (array[j][i] == 0){continue;}else{Vector_Sub(array[j], array[i], array[j][i] / array[i][i], 2 * n);}}}}for (i = 0; i < n; i++){temp = array[i][i];for (j = i; j < 2 * n; j++){array[i][j] = array[i][j] / temp;}}for (i = 0; i < n - 1; i++){for (j = i + 1; j < n; j++){Vector_Sub(array[i], array[j], array[i][j], 2 * n);}}for (i = 0; i < n; i++){for (j = 0; j < n; j++){result[i][j] = array[i][j + n];}}Matrix_Free(array, n, n);for (i = 0; i < n; i++){for (j = 0; j < n; j++){array1[i][j] = array1_temp[i][j];}}Matrix_Free(array1_temp, n, n);return result;
}
float Matrix_Det(float **array, int n)
{int i, flag_det, flag_zero, j;flag_det = 0;flag_zero = 0;float temp, sum;sum = 1.0;//复制一份arrayfloat **array_temp = (float **)malloc(n * sizeof(float *));for (i = 0; i < n; i++){array_temp[i] = (float *)malloc(n * sizeof(float));}for (i = 0; i < n; i++){for (j = 0; j < n; j++){array_temp[i][j] = array[i][j];}}for (i = 0; i < n - 1; i++){for (j = i; j < n; j++){if (array[j][i] != 0){if (j == i){break;}else{swap(array[i], array[j], n);flag_det++;break;}}else{flag_zero++;if (flag_zero == n - i){return 0;}}}flag_zero = 0;for (j = i + 1; j < n; j++){if (array[j][i] == 0){continue;}else{Vector_Sub(array[j], array[i], array[j][i] / array[i][i], n);}}}for (i = 0; i < n; i++){sum = sum*array[i][i] * pow(-1, flag_det);}for (i = 0; i < n; i++){for (j = 0; j < n; j++){array[i][j] = array_temp[i][j];}}Matrix_Free(array_temp, n, n);return sum;
}
void swap(float *src, float *dst, int n)
{int i;float temp;for (i = 0; i < n; i++){temp = src[i];src[i] = dst[i];dst[i] = temp;}
}
void Vector_Sub(float *src, float *dst, float value, int n)
{int i;for (i = 0; i < n; i++){src[i] = src[i] - dst[i] * value;}
}
int Matrix_Free(float **tmp, int m, int n)
{int i, j;if (tmp == NULL){return(1);}for (i = 0; i < m; i++){if (tmp[i] != NULL){free(tmp[i]);tmp[i] = NULL;}}if (tmp != NULL){free(tmp);tmp = NULL;}return(0);
}

---

三 结果

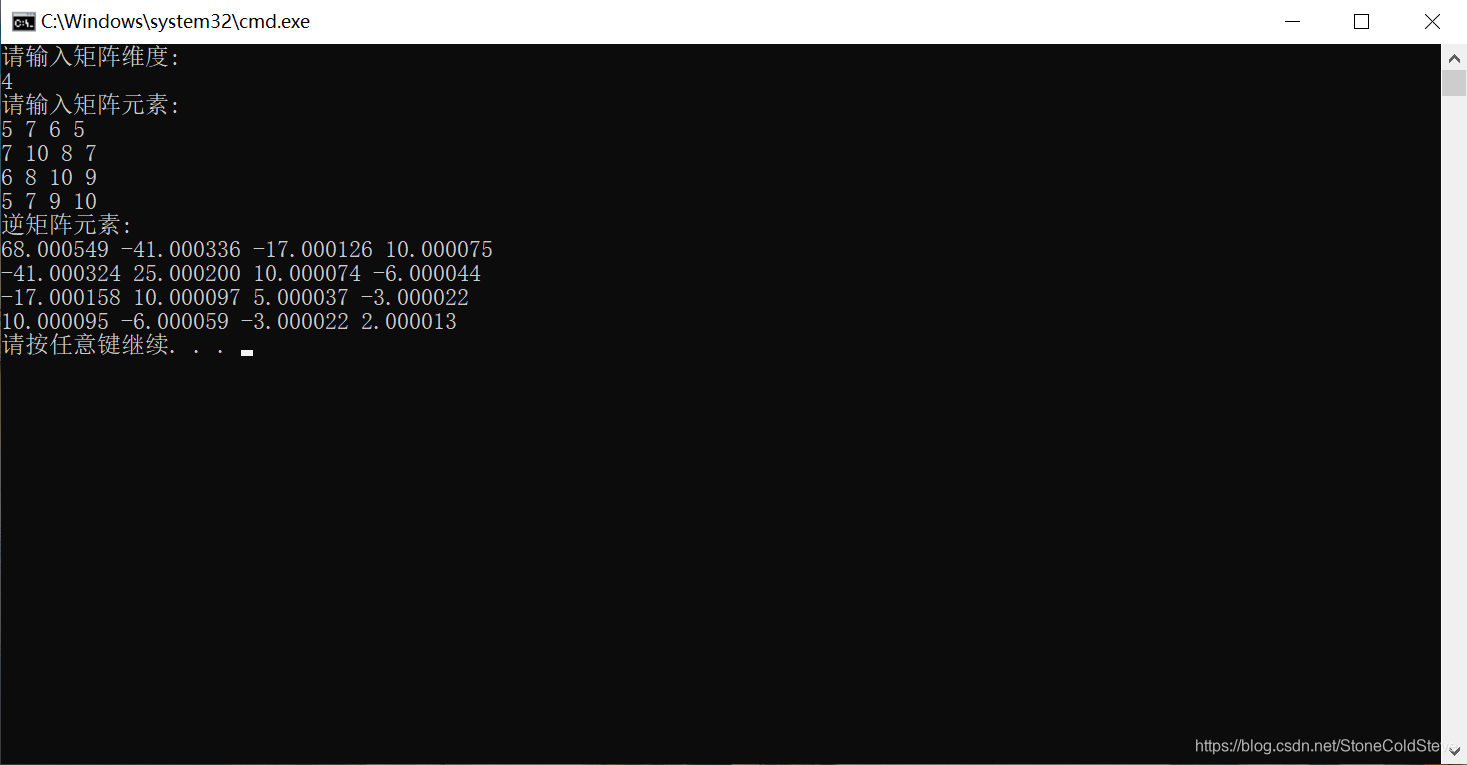
这篇关于高斯消元法求矩阵的逆矩阵C语言实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---