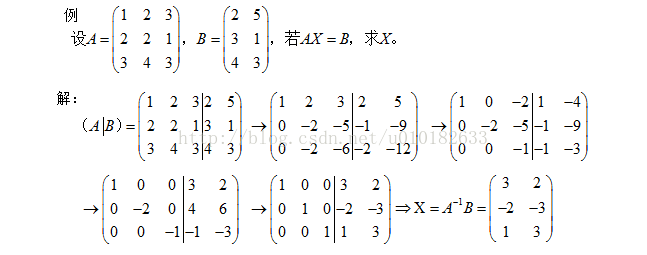元法专题

数学基础 -- 积分计算之换元法

换元积分法换元积分法是一种通过变量替换将复杂的积分问题转化为相对简单的积分问题的技巧。该方法的核心思想是通过选取合适的替换变量，将原积分的被积函数形式简化，进而方便计算。换元法的步骤选取替换变量：分析被积函数的形式，选择一个合适的替换变量 u = g ( x ) u = g(x) u=g(x)，使得原积分可以在新的变量下表达为一个较为简单的积分。求导并替换微分：计算所选变量的导

漫步微积分二十一——不定积分和换元法

如果 y=F(x) y=F(x)是导数已知的函数，例如 ddxF(x)=2x(1) \begin{equation}\frac{d}{dx}F(x)=2x\tag1\end{equation}我们能够知道函数 F(x) F(x)？不需要多想我们就能写出符合要求的函数，即 F(x)=x2 F(x)=x^2。更进一步，添加一个常数不会改变导数结果，所以下面的所有函数

分别用高斯消元法和列主元消去法求解，（自制）表格比较两种算法的结果与精度，分析实验出现的问题，并总结解决办法。

以下是一个使用高斯消元法和列主元消去法求解线性方程组的示例：假设我们要解决以下线性方程组： 4x + 2y + z = 8 -2x + y - 3z = -11 3x - 2y + 4z = 10 首先，我们可以将该线性方程组表示为增广矩阵的形式： [4 2 1 | 8] [-2 1 -3 | -11] [3 -2 4 | 10] 使用高斯消元法，我们可以进行以下操作：将第一个方程

高等数学——求解不定积分的经典换元法

本文始发于个人公众号：TechFlow，原创不易，求个关注今天是高等数学专题的第九篇文章，我们继续来看不定积分。在上篇文章当中我们回顾了不定积分的定义以及简单的性质，我们可以简单地认为不定积分就是求导微分的逆操作。我们要做的是根据现有的导函数，逆推出求导之前的原函数。除了基本定义之外，我们还介绍了一些简单的性质和常用积分的积分表。但是显然根据已有的性质对于许多复杂的函数来说求解积分

高斯消元法的应用

如果有这么一个线性规划系统的例子：添加图片注释，不超过 140 字（可选）将如上的线性规划系统转换为：添加图片注释，不超过 140 字（可选）这里要注意的是转换后的约束条件全部都变成了等号的约束，它与前面用的高斯消元法的方程组很相似，约束条件所形成的方程组有4个变量，但是只有两个方程，因此这个方程组有无限的解，这里只关注一些具有特定性质的解。一些特定的解，就是把

高斯消元法求矩阵的逆矩阵C语言实现

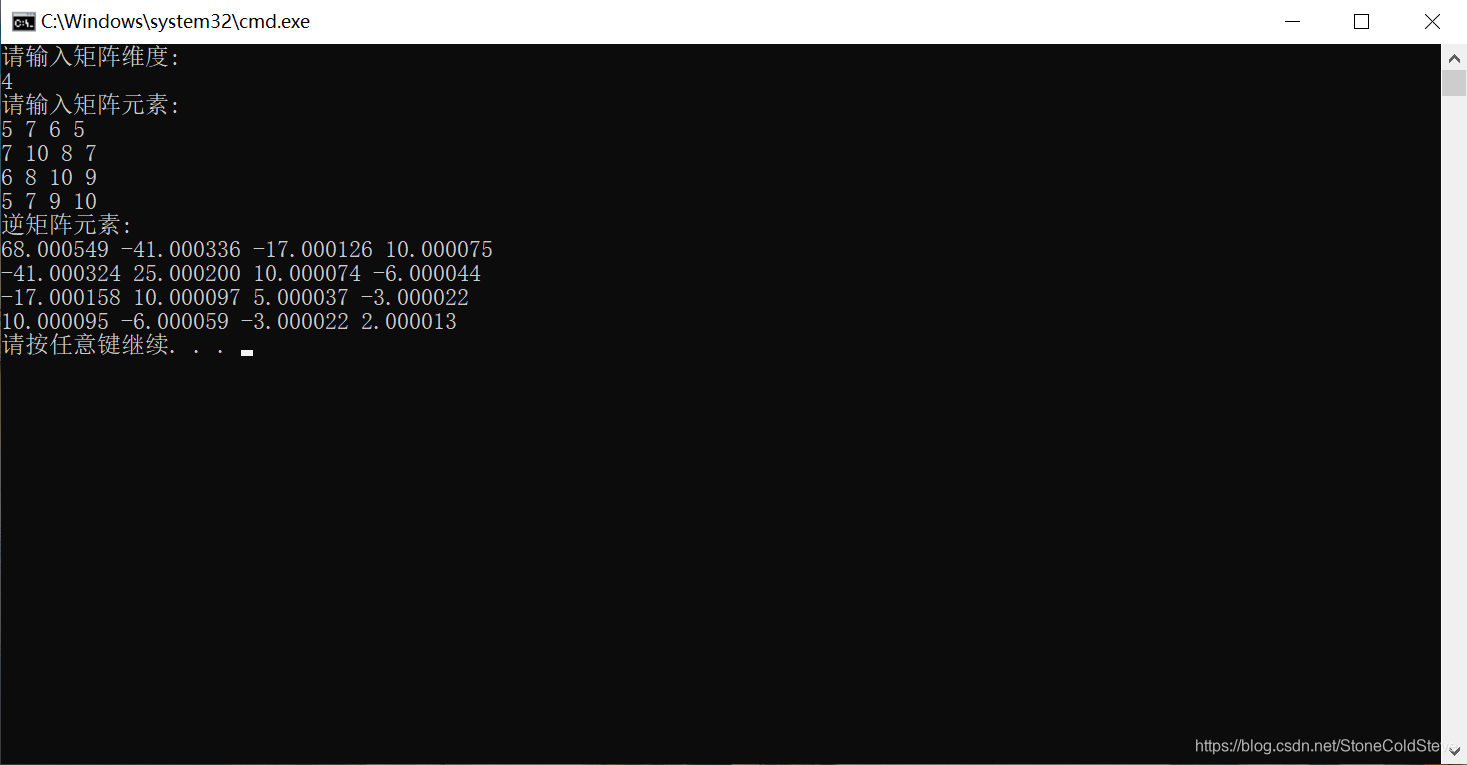
一原理在大学的线性代数课程中我们学习到了,想求一个 n n n维方阵的逆矩阵(如果存在的话),一种可行的方法是将其与一个对应维度的单位矩阵进行列的拼接,然后对所拼接的矩阵只进行初等的行变换并且当左侧的矩阵变换成为 n n n维的单位矩阵时,右侧的矩阵则为待求的逆矩阵,见式(1-1-1),其中矩阵 A A A是一个 n n n阶的方阵. 二 C语言实现 #include<stdio

二元一次方程高斯消元法计算函数

TRS = array [ 1..2 ] of Real ; {二元一次方程高斯消元法计算函数} function X1Y1_2 ( const ia1 , ib1 , ic1 , ia2 , ib2 , ic2 : Real ): TRS ; const //为数组的行数与列数 Row

js 解二元一次方程组（消元法）

解二元一次方程，首先想到的就是消元法确定好消元法，就按照消元法制定算法二元一次方程结构为 ax + by = ckx + fy = s x和y为变量，a、b、c、k、f、s、为常量 1.确定常量，用户输入|定义常量 let a = 2,b = 3,c = 13,k = 3,f = 4,s = 18 2.取 a和k（或者 b和f）的最大公约数，消掉 x （或者y），这举出

高斯消元法(Gauss Elimination)【超详解模板】

高斯消元法，是线性代数中的一个算法，可用来求解线性方程组，并可以求出矩阵的秩，以及求出可逆方阵的逆矩阵。高斯消元法的原理是：若用初等行变换将增广矩阵化为，则AX = B与CX = D是同解方程组。所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解。 1、线性方程组 1）构造增广矩阵，即系数矩阵A增加上常数向量

高斯消元法和列主销元法（Python实现）

目录 1、原理（1）思维导图（2）原理 2、案例及实现（1）案例（2）代码实现（3）结果 3、误差分析及心得体会 1、原理（1）思维导图（2）原理 2、案例及实现（1）案例（2）代码实现 import numpy as np# 判断系数矩阵是否为非奇异矩阵def IsItNonSingular(A):row = len

高斯削元法

例子：证明 ∣ 1 1 1 1 a b c d a 2 b 2 c 2 d 2 a 4 b 4 c 4 d 4 ∣ = ( a − b ) ( a − c ) ( a − d ) ( b − c ) ( b − d ) ( c − d ) ( a + b + c + d ) 证明 \begin{vmatrix} 1 & 1 & 1&1 \\a&b&c&d\\a^2&b^2&c^2&d^2\\

定积分的应用@元素法@微元法@平面图形面积

文章目录 abstract微元法(元素法)微元法的步骤平面图形的面积直角坐标系上图形面积参数方程确定的曲线所围成的图形面积例极坐标上图形面积👺曲边扇形面积曲扇环面积应用例例 abstract 微元法定积分的应用@平面图形面积@体积@弧长微元法(元素法) 定积分(一重,二重,三重积分)应用的关键在于微元法设所求的量 F F F依赖于区间 [ a , b ] [a

换元法解基本不等式求范围二例_Simplelife_新浪博客

练习：

换元法求不定积分

1.一般步骤：选取换元对象（不一定是式子中的值，也可以是式子中的最小公倍数或者最大公因数），然后将dx换为dt*t的导数，再用t将原式表示，化简计算即可 2. 3. 4. 5. 6.

高斯消元(完全主元法 and 部分主元法) C++代码

部分主元法高斯消元 /*算法步骤：1.枚举每一列，找到绝对值最大的一行2.将该行和第一行交换3.将该行行首置为一4.将下面所有行第 i 列置为零*/#include <iostream>#include <cmath>using namespace std;const int N = 109;const double eps = 1e-6;double a[N][N];int n;

六角幻方（高斯消元法求解）

看了网上很多都是用dfs解决的，于是自己就写了一篇用高斯消元法的解决方法问题描述把 1 2 3 … 19 共19个整数排列成六角形状，如下：要求每个直线上的数字之和必须相等。共有15条直线哦！再给点线索吧！我们预先填好了2个数字，第一行的头两个数字是：15 13，参见下图，黄色一行为所求。请你填写出中间一行的5个数字。数字间用空格分开。这是一行用空格分开的整数，请通过浏览器

$不定积分第一类换元法（凑微分法）$

元法专题

数学基础 -- 积分计算之换元法

漫步微积分二十一——不定积分和换元法

分别用高斯消元法和列主元消去法求解，（自制）表格比较两种算法的结果与精度，分析实验出现的问题，并总结解决办法。

高等数学——求解不定积分的经典换元法

高斯消元法的应用

高斯消元法求矩阵的逆矩阵C语言实现

二元一次方程高斯消元法计算函数

js 解二元一次方程组（消元法）

高斯消元法(Gauss Elimination)【超详解模板】

高斯消元法和列主销元法（Python实现）

高斯削元法

定积分的应用@元素法@微元法@平面图形面积

换元法解基本不等式求范围二例_Simplelife_新浪博客

换元法求不定积分

高斯消元(完全主元法 and 部分主元法) C++代码

六角幻方（高斯消元法求解）

不定积分第一类换元法（凑微分法）

【数值计算方法】Gauss消元法及其Python/C实现

AM@微元法和定积分的应用@平面图形面积@立体体积@曲线弧长

2.2 消元法的概念

矩陣分析-線性系統-2 高斯消元法、高斯－若爾當消元法

matlab高斯消元法求解线性方程组