本文主要是介绍高斯消元法的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
如果有这么一个线性规划系统的例子:
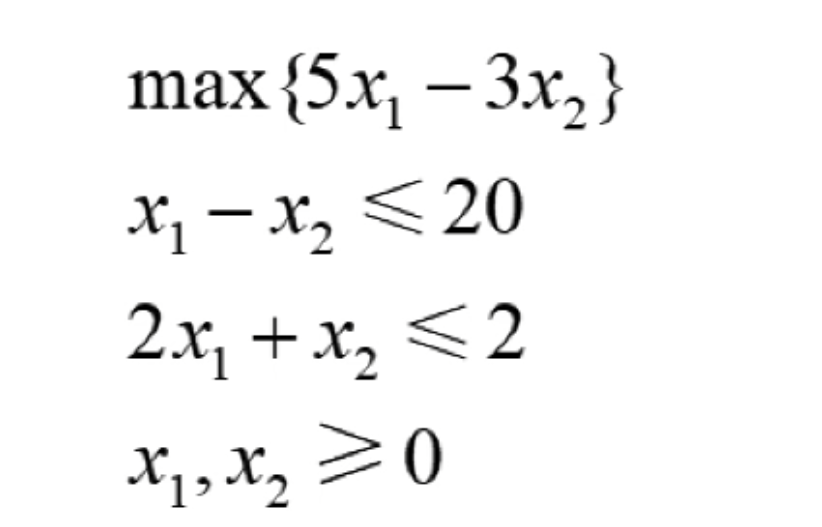
添加图片注释,不超过 140 字(可选)
将如上的线性规划系统转换为:
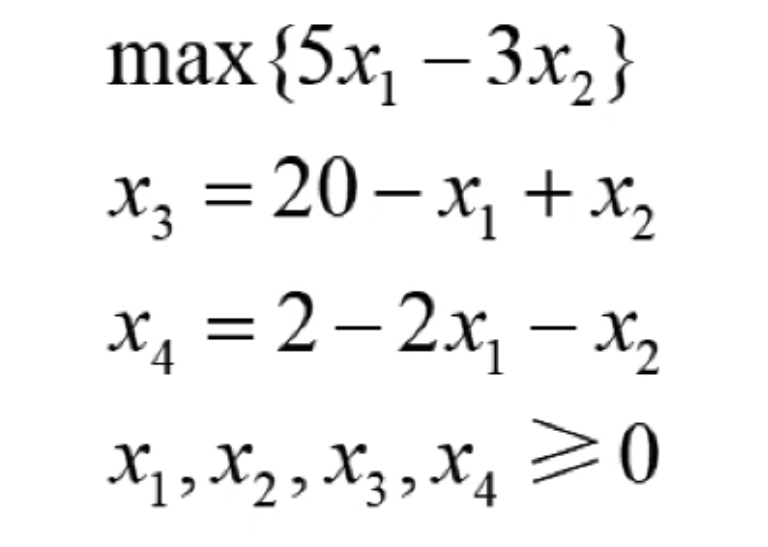
添加图片注释,不超过 140 字(可选)
这里要注意的是转换后的约束条件全部都变成了等号的约束,它与前面用的高斯消元法的方程组很相似,约束条件所形成的方程组有4个变量,但是只有两个方程,因此这个方程组有无限的解,这里只关注一些具有特定性质的解。
一些特定的解,就是把约束条件等号右边变量全部设置为0,然后得到等号左边变量的值,这种解也就是基本解,例如,将x1和x2设置为0,然后就得到了x3=20,x4=2,因此得到的一组基本解。
根据这组基本解,就有了目标函数的值是0,接下来要在这组基本解上反复的迭代变换,直到最后得到让目标条件最大化的解,从目标函数中找到一个系数为正数的变量,例如当前目标函数中的x1的系数是5,选中这个变量。
然后再不破坏约束条件的情况下,尽可能增加它的值,在x1增加时有可能会导致其他变量减
这篇关于高斯消元法的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



