本文主要是介绍换元法求不定积分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.一般步骤:选取换元对象(不一定是式子中的值,也可以是式子中的最小公倍数或者最大公因数),然后将dx换为dt*t的导数,再用t将原式表示,化简计算即可
2.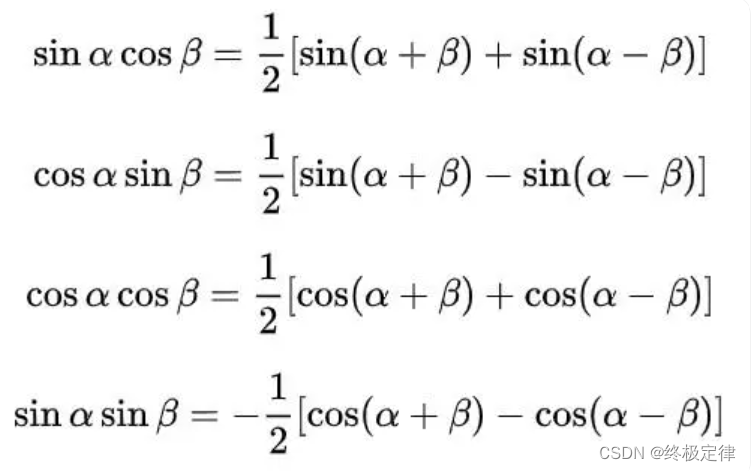
3.
4.
5.
6.
这篇关于换元法求不定积分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
本文主要是介绍换元法求不定积分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.一般步骤:选取换元对象(不一定是式子中的值,也可以是式子中的最小公倍数或者最大公因数),然后将dx换为dt*t的导数,再用t将原式表示,化简计算即可
2.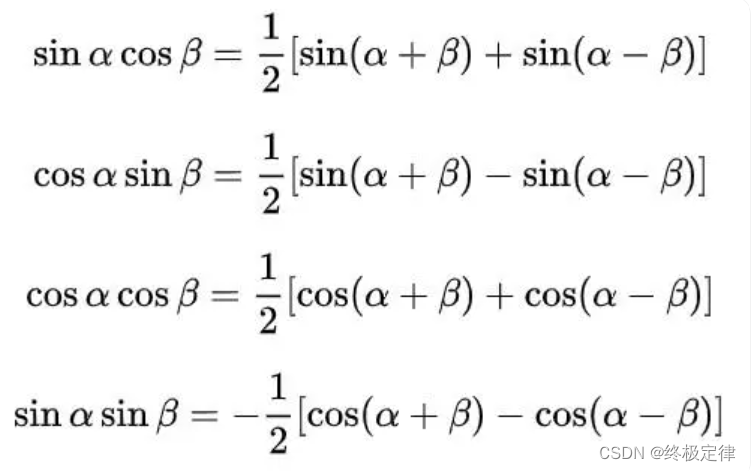
3.
4.
5.
6.
这篇关于换元法求不定积分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
http://www.chinasem.cn/article/458663。
23002807@qq.com