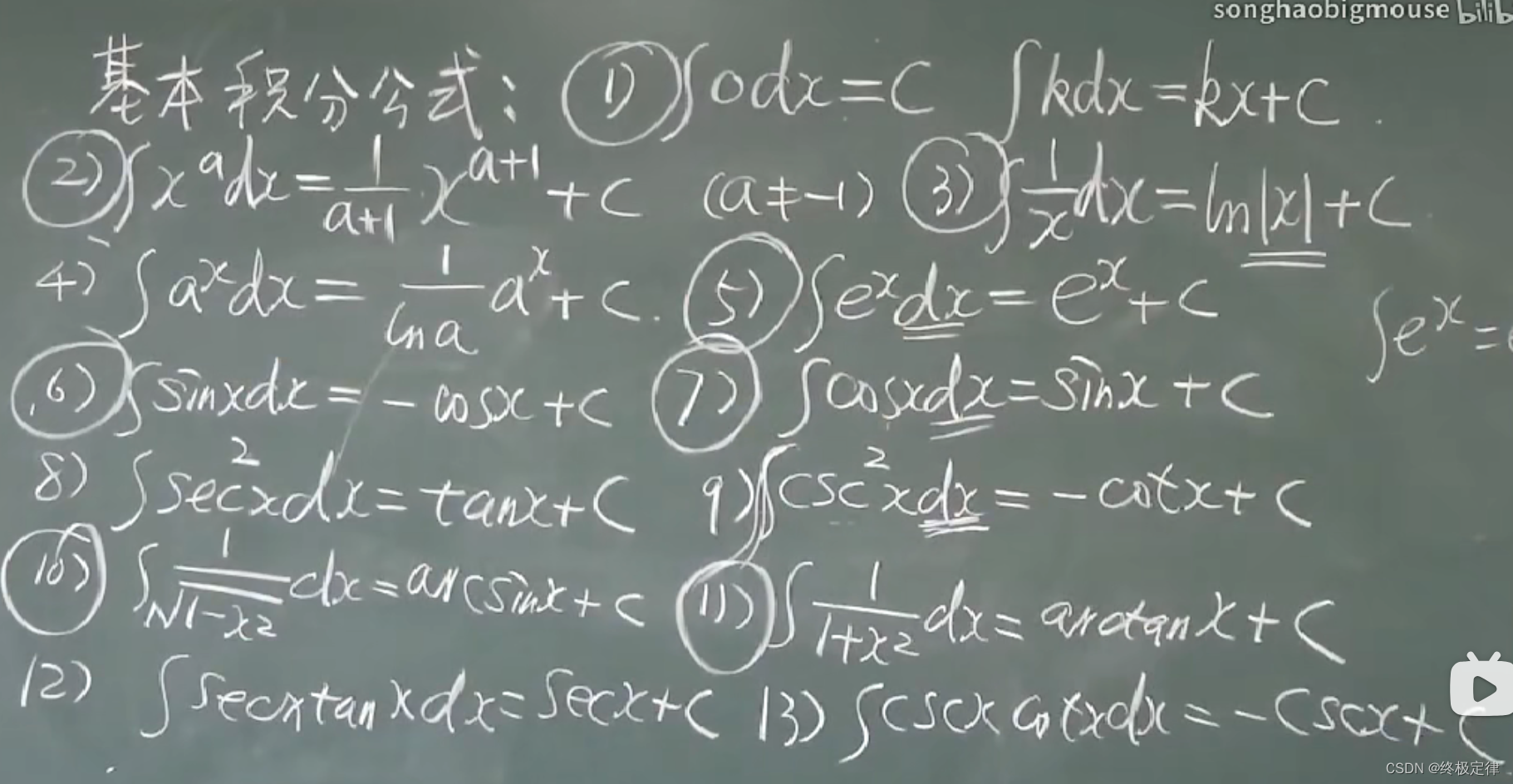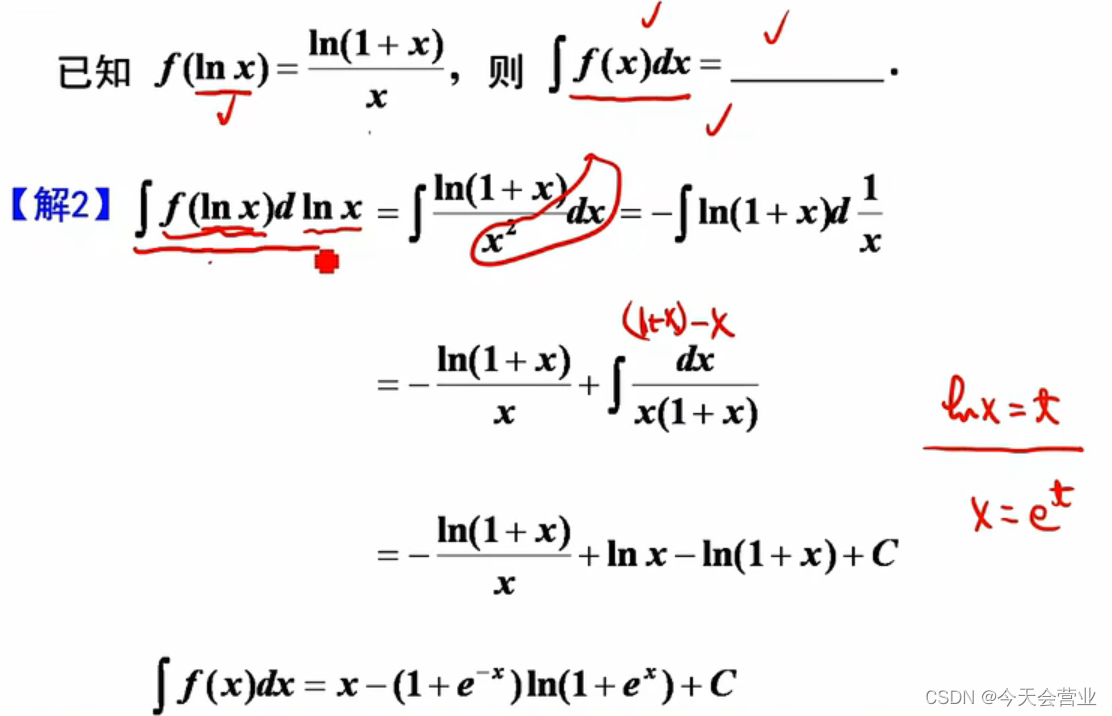不定积分专题

证明不定积分收敛

证明不定积分收敛 @(微积分) 证明：若 ∫101xpdx \int_0^1\frac{1}{x^p}dx收敛，则p<1 分析：p=1时， ∫10

漫步微积分二十一——不定积分和换元法

如果 y=F(x) y=F(x)是导数已知的函数，例如 ddxF(x)=2x(1) \begin{equation}\frac{d}{dx}F(x)=2x\tag1\end{equation}我们能够知道函数 F(x) F(x)？不需要多想我们就能写出符合要求的函数，即 F(x)=x2 F(x)=x^2。更进一步，添加一个常数不会改变导数结果，所以下面的所有函数

第三章一元函数积分学，第一节不定积分积分方法，第一类还原法

1. 不定积分积分方法 1.1 第一类还原法 1.1.1定理 1.1.2 例子

观看考研高数教学视频，练习不定积分常考题型与典型例题

所做笔记如下：

高等数学——求解不定积分的经典换元法

本文始发于个人公众号：TechFlow，原创不易，求个关注今天是高等数学专题的第九篇文章，我们继续来看不定积分。在上篇文章当中我们回顾了不定积分的定义以及简单的性质，我们可以简单地认为不定积分就是求导微分的逆操作。我们要做的是根据现有的导函数，逆推出求导之前的原函数。除了基本定义之外，我们还介绍了一些简单的性质和常用积分的积分表。但是显然根据已有的性质对于许多复杂的函数来说求解积分

高等数学——微积分中的不定积分

本文始发于个人公众号：TechFlow，原创不易，求个关注今天是高等数学专题的第8篇文章，今天的内容是不定积分。我之前的高数老师曾经说过，高等数学就是大半本的微积分加上一些数列和极限的知识。而微积分当中，积分相关又占据了大半江山。微积分之所以重要并不是因为它的比重大、容量多，而是因为它常用。几乎所有理工科的课本上都有微积分的公式，原因也很简单，当年这些科学家在研究未知事物或者是进行计算

$一篇文章帮你搞懂：f(x)存在、f‘(x)存在、原函数（不定积分）存在、定积分存在$

一篇文章帮你搞懂：f(x)存在、f‘(x)存在、原函数（不定积分）存在、定积分存在

目录 1、f(x)存在 2、f'(x)存在 3、原函数（不定积分）存在定理 4、定积分存在定理 1、f(x)存在（1）f(x)在一点极限存在 ≠> f(x)在这一点连续（2）f(x)存在 ≠> f(x)有介质性（3）f(x)可导 + => f'(x)在x0连续证明： 2、f'(x)存在（1）f'(x)存在 => f'(x)有介质性（达

考研 | 高等数学 Chapter4 不定积分

考研 | 高等数学 Chapter4 不定积分文章目录考研 | 高等数学 Chapter4 不定积分I. 定义II. 不定积分工具a. 基本公式b. 积分法case1: 第一类换元积分法case2: 第二类换元积分法1. **无理变有理**2. **三角代换, 平方和平方差**3. **分部积分法** III. 特殊函数的不定积分a. 有理函数case1: 假分式case2: 真分

不定积分例子

∫ sec ⁡ x d x = ∫ 1 cos ⁡ x d x = ∫ cos ⁡ x cos ⁡ 2 x d x = ∫ cos ⁡ x ( 1 + sin ⁡ x ) ( 1 − sin ⁡ x ) d x = 1 / 2 ∫ cos ⁡ x 1 + sin ⁡ x d x + 1 / 2 ∫ cos ⁡ x 1 − sin ⁡ x d x = 1 / 2 ln ⁡ ∣ 1 + sin ⁡

$考研数学——高数：不定积分$

考研数学——高数：不定积分

一、换元定积分法 ①第一类换元法定理1 若则这个方法也叫凑微分法，实际运用中是将被积函数的一部分拿到d的后面（相当于对部分求积分）然后将d之后的部分看成一个整体，再对原函数积分，起到化简的效果例题（求下列不定积分） ②

正式阶段高等数学复习之不定积分

不定积分这部分是为后面的定积分做准备的，整体上的框架可以分为2（定义）+3（计算方式）+3（能积出来的三个函数） 1、不定积分的概念：求某一个函数的不定积分就是求这个函数的原函数，那这里就牵扯到了存在性的问题，什么函数一定有不定积分即原函数？第一，连续的函数一定有原函数，因为连续，所以这个函数的变上限积分函数的导数等于这个函数，因此变上限积分函数就是一个原函数（这里会有一个题型，给我们一个连续的

$《微积分：一元函数积分学》——不定积分与定积分的存在定理$

《微积分：一元函数积分学》——不定积分与定积分的存在定理

1、原函数（不定积分）存在定理（1）连续函数 f(x) 必有原函数 F(x) （2）含有第一类间断点、无穷间断点的函数 f(x) 在包含该间断点的区间内必没有原函数 F(x) 2、定积分存在定理（1）f (x) 在 [a,b] 上连续，则存在（2）若 f (x) 在 [a,b] 上有界，且只有有限个间断点则存在另一个充要条件：若 f (x)在 [a,b] 上

换元法求不定积分

1.一般步骤：选取换元对象（不一定是式子中的值，也可以是式子中的最小公倍数或者最大公因数），然后将dx换为dt*t的导数，再用t将原式表示，化简计算即可 2. 3. 4. 5. 6.

不定积分（注意定义域）

1.符号为拉长的s 2.不定积分其实是已知导数求原函数，定义域必须相同 3.几何意义，所有的原函数在同一个x处切线斜率相同 4.性质：导数求原函数再求导为导数 5.对原函数的导数求积分为原函数 6.被积函数中有常数可以提到积运算外面，但常数不能与x有关如x的倍数 7.多个函数的和不定积分等于多个函数不定积分的和（有限个） 8.

$不定积分第一类换元法（凑微分法）$

不定积分第一类换元法（凑微分法）

将其中的分解为相当于令那么. 就可以得到例题1 令那么因为所以利用基本积分公式结果例题2 上下同除接下来需要一些技巧这个形式需要联想到一个基本积分公式不巧是这里是2不是1需要利用技巧把2变成1

考研数学第四、五章复习：不定积分与定积分

这一块应该说是基础中的基础了。我不想说太多，只把简要的重点的再强调一遍。目录一、不定积分与定积分存在定理比较以及其他定义方面的比较二、定积分的几何意义三、不定积分与定积分的性质比较一、不定积分与定积分存在定理比较以及其他定义方面的比较既然谈到不定积分，我们就无法避免提及原函数的概念。原函数存在定理：如果函数f(x)在区间I上连续，那么在区间I上存在可导函数F(x)

$《微积分：一元函数积分学》——不定积分与定积分的存在定理$