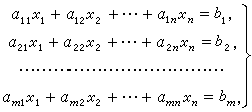To xor or not to xor 高斯消元求异或

本文主要是介绍To xor or not to xor 高斯消元求异或，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【题目】

给你n个long long范围内的整数，你可以选取1个或多个数进行异或操作，使得结果最大，求最大的结果。

【题目分析】

真是一道好题，不是真正理解高斯消元是无法做这题的。
题意：给你n个数，可以选择任意个数异或，但是要使得最后的异或值最大。
我们把每个数用二进制表示，要使得最后的异或值最大，就是要让高位尽量为1，高位能不能为1就必须用高斯消元判断了。
1. 根据数的二进制表示，建立方程组的矩阵，结果那列置为1。
2. 从下往上高斯消元(高位放下面)，如果该行有未被控制的变元，则该行的结果一定为1，且该变元控制该行。
3. 从该行往上依次消掉(异或)该变元。
4. 如果该行没有可以用来控制的变元，如果最后一列是0，则该行结果也为1，否则该行结果为0。这里能抱着已用来控制的变元的系数全是0，因为在第3步时就消掉该行以上此列的0了，后面0与0以后还是0。所以如果最后一列是0, 即该行方程也可以成立，故结果为1。
建立方程：
a11x1+a21x2……=d[1]
a12x1+a22x2……=d[2]
……

【代码】

#include<iostream>
#include<cstdlib>
#include<stdio.h>
#include<memory.h>
#define ll long long
using namespace std;
int equ,var;
int n;
int a[62][105];
bool vis[105];
void gauss()
{ll ans=0;int i,j,k;for(i=equ-1;i>=0;i--){ans<<=1;for(j=0;j<var;j++){if(a[i][j]&&!vis[j]){vis[j]=true;ans|=1;break;}}if(j==var){if(a[i][var]==0) ans|=1;}else{for(k=i-1;k>=0;k--){if(a[k][j]){for(int l=0;l<var+1;l++)a[k][l]^=a[i][l];}}}}// cout<<equ<<" "<<var<<"*"<<endl;cout<<ans<<endl;
}
void init()
{ll m;var=n;//n个数，所以n个未知数equ=0;int k;for(int i=0;i<n;i++){cin>>m;k=0;while(m!=0){int j=m&1;a[k++][i]=j;m>>=1;}if(k>equ) equ=k;}for(int i=0;i<equ;i++)a[i][var]=1;
}
int main()
{freopen("in.txt","r",stdin);while(scanf("%d",&n)!=EOF){memset(a,0,sizeof(a));memset(vis,false,sizeof(vis));init();gauss();}
}

【后记】

好好理解高斯消元求余的用法

下面介绍一种yy的方法（非高斯消元）（来自高老板）：

【代码】

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
const int maxn=110;
LL a[maxn];
int n;
int main() {while(scanf("%d",&n)!=EOF) {for(int i=1; i<=n; i++)scanf("%lld",&a[i]);for(int i=1; i<=n; i++) {int tmp=i;for(int j=i+1; j<=n; j++)if(a[j]>a[tmp])tmp=j;swap(a[i],a[tmp]);for(int j=i+1; j<=n; j++)a[j]=min(a[j],a[i]^a[j]);}LL ans=0;for(int i=1; i<=n; i++)ans=max(ans,ans^a[i]);printf("%lld\n",ans);}return 0;
}

【后记】具体代码是做什么用的，没有看太明白。

下面是根据上面代码进行了一下优化：

【代码】

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
long long f[150];
int main() {int n, i, j;while(cin>>n) {for(i=0; i<n; i++)cin>>f[i];sort(f,f+n);for(i=0; i<n; i++) {for(j=i+1; j<n; j++)//if((f[i]^f[j]) <f[j])f[j]=min(f[j],f[i]^f[j]);}long long ans=0;for(i=0; i<n; i++)ans=max(ans,ans^f[i]);cout<<ans<<endl;}return 0;
}

这篇关于To xor or not to xor 高斯消元求异或的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---