本文主要是介绍acwing数学知识(三) 高斯消元 求组合数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.高斯消元
描述:解一个包含n个方程n个未知数的线性方程组

算法流程:对每一列的系数进行如下操作
1.找到一列中系数绝对值最大的一条方程(不考虑已经移动过的方程)
2.将其移到最上方(同样不考虑移动过的方程)
3.将该系数变为1
4.将下面的方程同一列的系数消为0
5.得到一个倒三角形方程组,即可求出解
得出三种情况:
①完美在倒三角i选哪个 唯一解
②0 = 非0 无解
③0 = 0 无穷解
#include <iostream>
#include <algorithm>
#include <cmath>using namespace std;const int N = 110;
const double e = 1e-6;int n;
double a[N][N];int gauss()
{int r , c; //r是行 c是列for(r = 0,c = 0 ; c < n ; c++ )//对每一列的系数进行操作{int t = r;//记录系数最大的那行for(int i = r ; i < n ; i++)//找系数最大的那行if(fabs(a[i][c]) > fabs(a[t][c])) t = i;if(fabs(a[t][c]) < e) continue;for(int i = c ; i <= n ; i++) swap(a[t][i] , a[r][i]);//将找到的那行跟最上面的那行交换for(int i = n ; i >= c ; i--) a[r][i] /= a[r][c];//把最前面的系数变成1,并且消掉后面的数for(int i = r + 1 ; i < n ; i++)//将下面的方程同一列的系数消为0,并且减掉后面的系数for(int j = n ; j >= c ; j--)a[i][j] -= a[i][c] * a[r][j];r++; //向下沉 }if(r < n){for(int i = r ; i < n ; i++)if(fabs(a[i][n]) > e) return 2;//无解return 1;//无数个解}for(int i = n - 1 ; i >= 0 ; i--)//最后利用倒三角形将每个数的解求出for(int j = i + 1 ; j < n ; j++)a[i][n] -= a[i][j] * a[j][n];return 0;//唯一解
}int main()
{cin >> n;for(int i = 0 ; i < n ; i++)for(int j = 0 ; j < n + 1 ; j++)cin >> a[i][j];int t = gauss();if(t == 0)for(int i = 0 ; i < n ; i++) printf("%.2lf\n" , a[i][n]);else if(t == 1) puts("Infinite group solutions"); else puts("No solution");return 0;
}
求组合数
1.题目:给定n组询问,每组询问给定两个整数a,b,请你输出Cba mod (109+7)的值。1≤n≤10000,1≤b≤a≤2000. O(N2)
数据较小,共有2000*2000=4e6中形式,直接暴力,先预处理每一种形式的值,再查询即可。
利用这条关系式:Cba = Cba-1 + Cb-1a-1,打个比方:Cba就是从a个苹果中拿b个,所有的拿法可以分成包括某个特殊的苹果,和不包括某个特殊的苹果,包括的情况则Cb-1a-1,不包括则是Cba-1,加起来就是Cba。
#include <iostream>using namespace std;const int N = 2010;
const int P = 1e9 + 7;
int t[N][N];int main()
{for(int i = 0 ; i < N ; i++)for(int j = 0 ; j <= i ; j++){if(!j) t[j][i] = 1;else t[j][i] = (t[j][i - 1] + t[j - 1][i - 1]) % P;//递推式}int n;cin >> n;while(n--){int a, b;cin >> a >> b;cout << t[b][a] << endl;}return 0;
}
2.题目:1≤n≤10000, 1≤b≤a≤105 (NlonN)
1e5 * 1e5 = 1e10,此时情况就太多了,就不能用之前的预处理了。
还知道Cba = a!/(b!*(a-b)!),所以我们可以预处理每一个数的阶乘先,然后在查询即可。
因为a/b mod p != (a mod p)/(b mod p),所以我们要转换成乘法,就要用到逆元。
#include <iostream>using namespace std;typedef long long ll;
const int N = 100010;
const int P = 1e9 + 7;int fact[N] , infact[N];//infact[i]是fact[i]的逆元,因为P是质数,所以可以用费马小定理,快速幂求逆元。int qmi(int a, int b , int p)//求
{int res = 1;while(b){if(b & 1) res = (ll)res * a % p;b >>= 1;a = (ll)a * a % p;}return res;
}int main()
{fact[0] = infact[0] = 1;for(int i = 1 ; i < N ; i++){fact[i] = (ll)i * fact[i - 1] % P;infact[i] = (ll)qmi(i , P - 2 , P) * infact[i - 1] % P;}int n;cin >> n;while(n--){int a , b;cin >> a >> b;cout << (ll)fact[a] * infact[b] % P * infact[a - b] % P << endl;}return 0;
}
3.题目:给定n组询问,每组询问给定三个整数a,b,p,其中p是质数,请你输出Cba mod p的值。1≤n≤20,1≤b≤a≤1018,1≤p≤105。
这里a和b的数据很大,要用到Lucas(鲁卡斯定理)
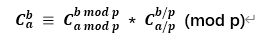
#include <iostream>using namespace std;typedef long long LL;int p;int qmi(int a, int b)//快速幂求逆元
{int res = 1;while(b){if(b & 1) res = (LL) res * a % p;b >>= 1;a = (LL) a * a % p;}return res;
}int C(int a , int b)
{if(a < b) return 0;int res = 1;for(int i = b , j = a ; i ; i-- , j--)//利用定义求出C{res = (LL) res * j % p;res = (LL) res * qmi(i , p - 2) % p;//利用逆元求}return res;
}int lucas(LL a, LL b)
{if(a < p && b < p) return C(a , b);return (LL)C(a % p , b % p) * lucas(a / p , b / p) % p;
}int main()
{int n;cin >> n;while(n--){LL a , b;cin >> a >> b >> p;cout << lucas(a , b) << endl;}return 0;
}4.题目:输入a,b,求Cba的值,1≤b≤a≤5000。
注意结果可能很大,需要使用高精度计算。
算法思路:
1.分解质因数,将Cba=a!/(b!*(a-b)!)分解质因数 p1k1 *p2k2 *p3k3 …pnkn ,求出最终每一个质因数的次数
2.高精度乘法
求a!中p的次数O(logp):
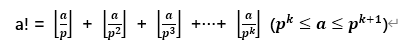
#include <iostream>
#include <vector>
#include <string>using namespace std;const int N = 5010;int primes[N];
int cnt;
int sum[N];
bool st[N];int get(int n , int p)//返回n的阶乘中 ,p的次数
{int s = 0;while(n){s += n / p;n /= p; }return s;
}vector<int> mul(vector<int> a , int b)//高精度乘法
{vector<int> ans;int t = 0;for(int i = 0 ; i < a.size() || t ; i++){if(i < a.size()) t += a[i] * b;ans.push_back(t % 10);t /= 10;}return ans;
}void get_primes(int n)//线性筛质数
{for(int i = 2 ; i <= n ; i++){if(!st[i]) primes[cnt++] = i;for(int j = 0 ; primes[j] * i <= n ; j++){st[primes[j] * i] = true;if(i % primes[j] == 0) break;}}
}int main()
{int a, b;cin >> a >> b;get_primes(a);for(int i = 0 ; i < cnt ; i++)//求出最终每一个p的次数{int p = primes[i]; sum[i] = get(a , p) - get(b , p) - get(a - b , p);}vector<int> res;res.push_back(1);for(int i = 0 ; i < cnt ; i++)//累乘for(int j = 0 ; j < sum[i] ; j++)res = mul(res , primes[i]);for(int i = res.size() - 1 ; i >= 0 ; i--) cout << res[i];cout << endl;return 0;
}
卡特兰数( Cn2n / (n+1))
题目:定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个。

举个栗子:n=6时,就可以画成上图,假设向右是0向上是1,则在红线以下的路径是合法的,可以看出每一条从(0,0)走到(6,6)的非法路径做关于红线的对称,都对应一条(0,0)-(5,7)的路径;反之,每一条从(0,0)-(5,7)的路径都对应一条从(0,0)-(6,6)的非法路径,那么就可以利用(0,0)-(5,7)的路径数间接求出(0,0)-(6,6)的非法路径数。
算法核心:每一条从(0,0)走到(n,n)的非法路径都对应一条从(0,0)走到(n-1,n+1)的非法路径,因此合法路径就是
因此从(0,0)走到(6,6)的不合法路径数就是Cn-12n,即合法的是Cn2n-Cn-12n ,化简得 Cn2n / (n+1),
所以直接从定义出发求出Cn2n ,其中因为模上一个质数,可以用快速幂求逆元。
#include <iostream>using namespace std;typedef long long LL;const int N = 100010 , mod = 1e9 + 7;int qmi(int a, int k, int p)
{int res = 1;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{int n;cin >> n;int ans = 1;for(int i = 2 * n ; i > n ; i--) ans = (LL) ans * i % mod;for(int i = n ; i >= 1 ; i--) ans = (LL) ans * qmi(i , mod - 2 , mod) % mod;ans = (LL) ans * qmi(n + 1 , mod - 2 , mod) % mod;cout << ans << endl;return 0;
}
这篇关于acwing数学知识(三) 高斯消元 求组合数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







