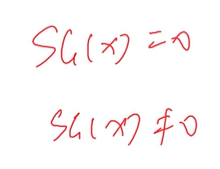数学知识专题
学习算法需要数学知识吗?
目录 算法与数学:看似不可分割的关系常见算法中的数学元素案例分析:不需要高深数学知识的算法1. 二分查找2. 深度优先搜索 (DFS)3. 动态规划:斐波那契数列 如何在有限的数学背景下学习算法1. 专注于算法的逻辑和过程2. 可视化算法流程3. 从简单的实现开始,逐步优化4. 学习算法设计模式5. 实践,实践,再实践6. 关注实际应用 数学如何帮助我们更好地理解和设计算法1. 算法复杂度
SAT数学知识范围分析
为了方便广大考生更好的复习，小编整理了SAT数学考题知识范围增量分析，以供各位考生备考SAT数学，希望对考生复习有所帮助。 美国高考SAT于今年3月份推出了新的SAT考试形式及内容，其中数学部分的考题范围与难易程度有所提高。以前的SAT数学考试程度仅相当于国内初三的数学水平，主要考学生的四则运算、因数、分数、百分数、小数及比率比值的基本知识及运算能力。这些数学的基本知识，对国内初三学生来
HTML5中手势原理分析与数学知识的实践
在这触控屏的时代，人性化的手势操作已经深入了我们生活的每个部分。现代应用越来越重视与用户的交互及体验，手势是最直接且最为有效的交互方式，一个好的手势交互，能降低用户的使用成本和流程，大大提高了用户的体验。 近期，公司的多个项目中都对手势有着较高的需求，已有的手势库无法完全cover，因此便撸了一个轻量、便于使用的移动端手势库。这篇博文主要是解析了移动端常用手势的原理，及从前端的角度学习过程中所使
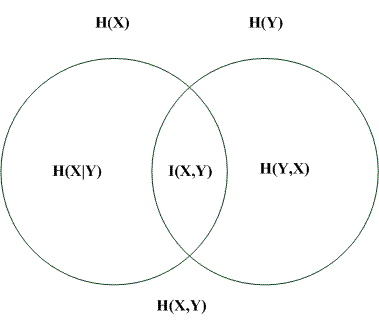
关于熵的一些数学知识
一些信息熵的含义 (1) 信息熵的定义：假设X是一个离散随即变量，即它的取值范围R={x1，x2...}是有限可数的。设pi=P{X=xi}，X的熵定义为： (a) 若(a)式中，对数的底为2，则熵表示为H2(x)，此时以2为基底的熵单位是bits，即位。若某一项pi=0，则定义该项的pilog
碰到的有用的数学知识积累
1. 这个公式，常用 2.e^x的泰勒展开 3.泰勒公式。 https://zh.wikipedia.org/wiki/%E6%B3%B0%E5%8B%92%E7%BA%A7%E6%95%B0 ---这些都经常碰到。 1. 定义 e 为下列 极限值： {\displaystyle e=\lim _{n\to \infty }\left(1+
从入门到高阶，读懂机器学习需要哪些数学知识
本篇文章想要说明的是数学并非认识世界的唯一途径，即使数学水平不高的你同样也可以开展机器学习方面的工作和研究。但是不可否认数学是自然科学领域探究真理的有效工具，有了强大的数学背景知识会让你看待问题更加深刻，这就是我们经常会看到很多大牛们都是出身数学专业。另外本文所列举的课程比较多，要想一下子去穷尽所有课程显然也不现实，大可不必打好所有的数学基础再去学机器学习，最好的做法是当你对机器学习本身的理解达到
掌握高等数学、线性代数、概率论所需数学知识及标题建议
在数学的广袤领域中，高等数学、线性代数和概率论作为三大核心分支，不仅在理论研究中占据重要地位，更在实际应用中发挥着举足轻重的作用。为了深入理解和掌握这三门学科，我们需要掌握一系列扎实的数学知识。 高等数学所需数学知识 高等数学是大学数学的重要组成部分，它以微积分为主要内容，研究函数、极限、导数、微分、积分等概念和方法。要学好高等数学，需要掌握以下数学知识： 基本代数知识：包括多项式的加减
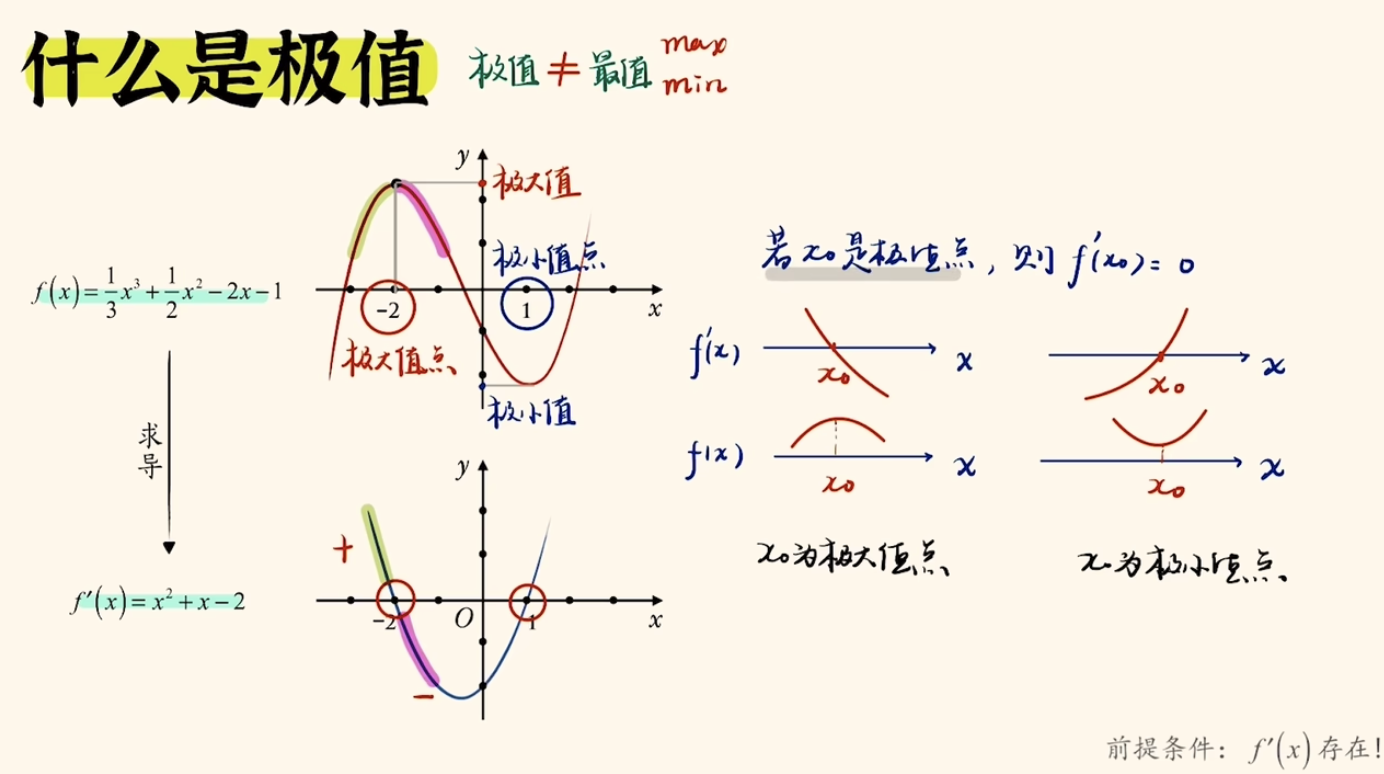
【重拾数学知识】导数、极值和最值
前言 在深度学习中，梯度下降法是一种常用的优化算法，用于更新模型参数以最小化损失函数。这梯度下降法中涉及到数学中的导数、极值等相关知识，因此我们重新回顾相关内容，以便加深理解。 相关概念 导数 一个问题 如何求得一个曲线f(x)中任意一点(x0)的斜率？ 核心思想：在曲线上另外存在一个P点，P点无限接近x0，x0和P的连线将无限接近x0点的斜率。 在上图中： 我们求x0点和
PR基本概念数学知识
§1、2基本概念 监督学习与非监督学习期望风险与经验风险结构风险最小化（SRM）与经验风险最小化（ERM）期望风险的上界过拟合数据预处理模型评价方法分类与聚类 数学知识 矩阵求逆、矩阵乘法协方差矩阵的计算特征值、特征向量的计算函数求偏导
笔试强训Day19 数学知识 动态规划 模拟
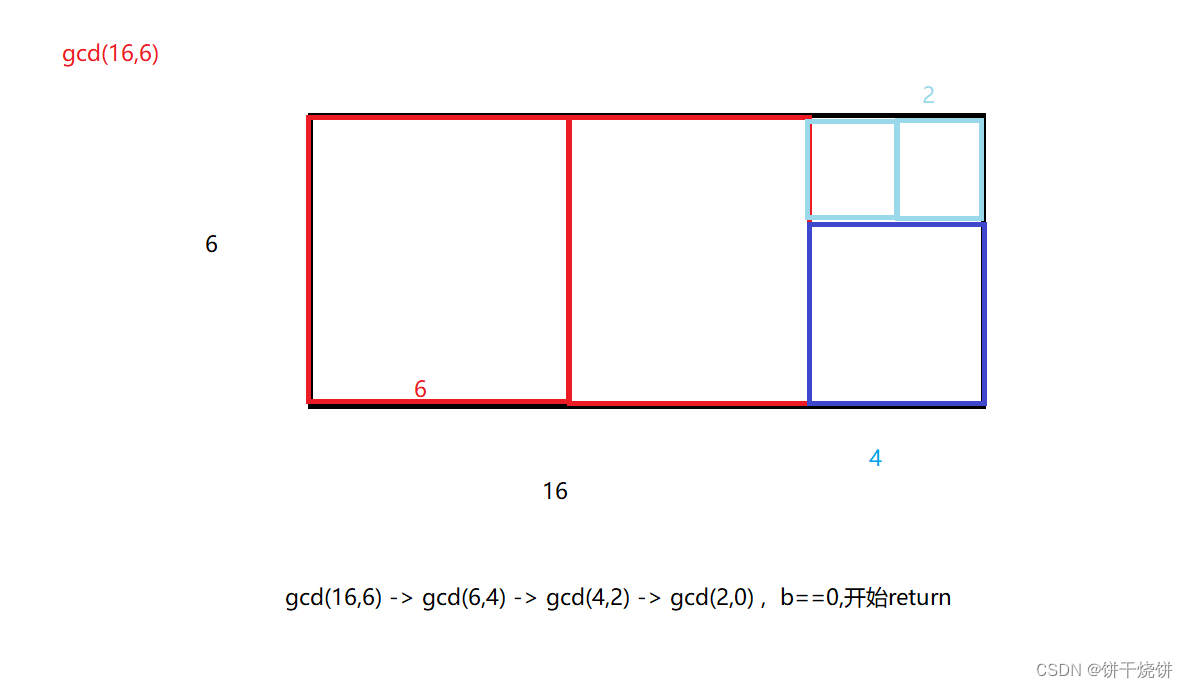
[编程题]小易的升级之路 题目链接：小易的升级之路__牛客网 思路： 按题目写即可 注意辗转相除法。 AC code： #include<iostream>using namespace std;int gcd(int a, int b){return b ? gcd(b, a % b) : a;}int main() {int n, a;while (scanf("%d%
acwing算法提高之数学知识--博弈论
目录 1 介绍2 训练 1 介绍 本博客用来记录博弈论相关的题目。 2 训练 题目1：1319移棋子游戏 C++代码如下， #include <cstdio>#include <cstring>#include <set>using namespace std;const int N = 2010, M = 6010;int n, m, k;int h[N], e[
【算法基础】第四章：数学知识
Chapter 4 数学知识 1：数论 质数（素数） 范围：从2开始的整数 定义：在大于1的整数中，只包含1和本身这两个约数 【1】质数的判定——试除法 bool is_prime(int x){if(n<2) return 0;for(int i=2;i<n;i++){if(n%i==0){return 0;}}return 1;} 时间复杂度：O(n) 优化！！
一文掌握机器学习必备数学知识（附学习资源）
来源：运筹OR帷幄 作者：留德华叫兽&王源 本文共5800字，建议阅读10分钟。本文划分了ML数学基础的的初、中、高三个阶段并提供针对各阶段的学习资源。 0.前言 本篇文章是由留德华叫兽在知乎的优秀回答改编扩展而成的，作者留德华叫兽有着应用数学和硕士运筹学、优化理论的背景转到德国海德堡大学读博，主要从事机器学习、计算机视觉的研究，希望自己的一些经验可以对想入门机器学习的朋友们有点借鉴作用。
数学知识--（欧拉函数，快速幂，扩展欧几里得算法）
本文用于记录个人算法竞赛学习，仅供参考 目录 一.欧拉函数 二.欧拉函数模板 三.用筛法求每个数的欧拉函数 四.快速幂 五.扩展欧几里得算法 六.用扩展欧几里得算法求线性同余方程 一.欧拉函数 即有一个数n， n通过质因数分解得到 通过欧拉函数有 证明：容斥原理 二.欧拉函数模板 实际上就是分解质因数 时间复杂度：O() //
数学知识--（质数，约数）
本文用于个人算法竞赛学习，仅供参考 目录 一.质数的判定 二.分解质因数 三.质数筛 1.朴素筛法 2.埃氏筛法 3.线性筛法 四.约数 1.求一个数的所有约数 2.约数个数和约数之和 3.欧几里得算法（辗转相除法）-- 求最大公约数 一.质数的判定 质数：质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的数。常见的质数有2, 3, 5,
canvas 中常用的数学知识
CanvasStudy 关于Canvas（About Canvas） Canvas API 提供了一个通过JavaScript和HTML的<canvas>元素来绘制图形的方式。它可以用于动画、游戏画面、数据可视化、图片编辑以及实时视频处理等方面。 Canvas API主要聚焦于2D图形。而同样使用<canvas>元素的 WebGL API 则用于绘制硬件加速的2D和3D图形。 Canvas
学校教的数学知识，编程用不到？
【文章来源微信公众号：每天学编程】 学校中所学的很多数学知识，在编程中用不到。 这儿是我能记得的在学校学到的数学： 初中：数，数数，算术知识，初级代数（“带问题的小故事”) 高中：代数，几何，高等代数，三角学，微积分先修课 (二次曲线论和极限) 大学：微积分，微分公式，线性代数，概率和统计，离散数学 上面那个关于高中数学课程单子上所列的，怎么来着？ 代数？是的。没问题。你需要代数
![[足式机器人]Part2 Dr. CAN学习笔记-Ch00-2 - 数学知识基础](https://img-blog.csdnimg.cn/direct/851b3f5b430849c29f34863b622acf42.png#pic_center)
[足式机器人]Part2 Dr. CAN学习笔记-Ch00-2 - 数学知识基础
本文仅供学习使用 本文参考： B站：DR_CAN 《控制之美(卷1)》 王天威 《控制之美(卷2)》 王天威 Dr. CAN学习笔记-Ch00 - 数学知识基础 Part2 4. Ch0-4 线性时不变系统中的冲激响应与卷积4.1 LIT System：Linear Time Invariant4.2 卷积 Convolution4.3 单位冲激 Unit Impulse——Dira
数学知识（四）（容斥原理、博弈论）
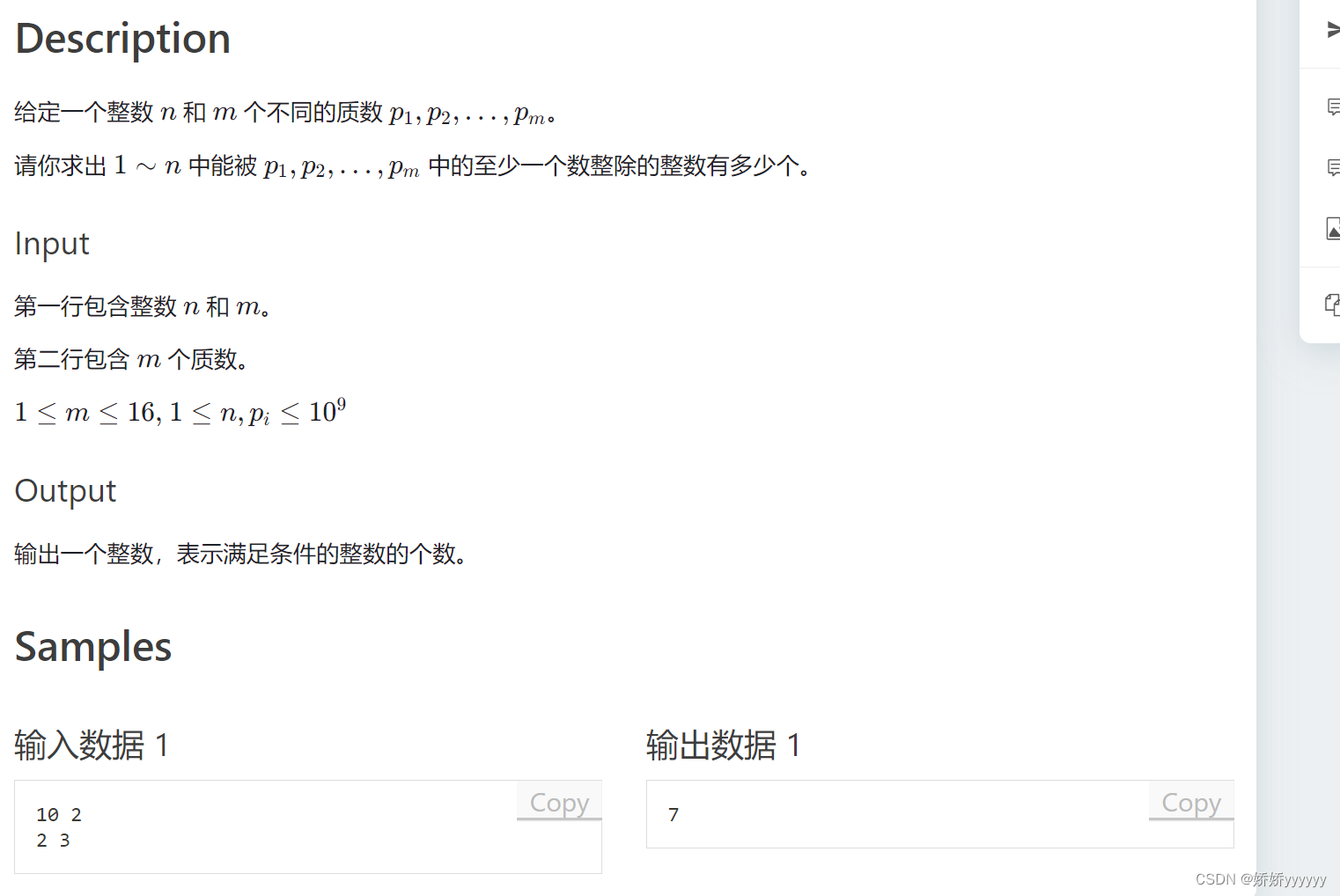
一、容斥原理 容斥原理公式 一共加或者减的式子个数 （一）利用容斥原理解决求能被质数整除的数的个数 890计算能被整除的数的个数 因为一共有2^n-1种选法，可以用位运算的方式枚举，对于得到的每一种选法，根据存在的数的个数判断前面是1还是-1。枚举到2^n-1的所有二进制数，判断每一位上的数是否是1， 最重要的转变是：将能被各个质数整除的集合看成一个个的集合。根据容斥原理
第四章 数学知识 （二）（欧拉函数、快速幂、扩展欧几里得、中国剩余定理）
一、欧拉函数（1~n中有多少个数和n互质） (一) 1~n 中和n互质的数 1、互质数：公约数为1的两个整数。 2、当n为6的时候： 3、容斥原理公式
人工智能基础部分24-人工智能的数学基础，汇集了人工智能数学知识最全面的概况
、 大家好，我是微学AI，今天给大家介绍一下人工智能基础部分24-人工智能的数学基础，汇集了人工智能数学知识最全面的概况，深度学习是一种利用多层神经网络对数据进行特征学习和表示学习的机器学习方法。要全面了解深度学习的数学基础，需要掌握这些数学知识：向量、矩阵、微积分、线性代数、概率论、数值计算、优化理论、信息论。 文章目录 第一章 数学基础1.1 向量和矩阵1.1.1 标量、向量、矩阵、
深度学习需要掌握的数学知识①【高等数学】
预备知识 1.集合的相关概念 集合是指具有某种特定性质的事物的总体，组成集合的事物称为集合的元素。 N表示自然数构成的集合，称为自然数集。 N = { 0 , 1 , 2 , … , n , … } N=\{ 0,1,2,\dots,n,\dots \} N={0,1,2,…,n,…}. N + N^{+} N+表示正整数集。 N + = { 1 , 2 , … , } N^{+}
数学知识第九期 容斥原理
前言 容斥原理在数学上经常会被提及，是一种很重要的数学知识。 一、容斥原理的基本内容 简介： 在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。 定