本文主要是介绍深度学习需要掌握的数学知识①【高等数学】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
预备知识
1.集合的相关概念
集合是指具有某种特定性质的事物的总体,组成集合的事物称为集合的元素。
N表示自然数构成的集合,称为自然数集。 N = { 0 , 1 , 2 , … , n , … } N=\{ 0,1,2,\dots,n,\dots \} N={0,1,2,…,n,…}.
N + N^{+} N+表示正整数集。 N + = { 1 , 2 , … , } N^{+}=\{ 1,2,\dots, \} N+={1,2,…,}.
在表示数集的字母右上方标"+"表示该数集内排除0与负数的集。
R表示全体实数构成的集合,称为实数集。
Z表示全体整数构成的集合,称为整数集。
Q表示全体有理数构成的集合,称为有理数集。 Q = { p q , p ∈ Z , q ∈ N + 且 p 与 q 互质 } Q=\{\frac{p}{q},p\in Z,q\in N^{+}且p与q互质 \} Q={qp,p∈Z,q∈N+且p与q互质}.
邻域: U ( x 0 , δ ) = { x ∣ ∣ x − x 0 ∣ < δ , δ > 0 } U(x_0,\delta)=\{ x|\;|x-x_0|<\delta,\delta>0 \} U(x0,δ)={x∣∣x−x0∣<δ,δ>0}.
去心邻域: U 。 = { x ∣ 0 < ∣ x − x 0 ∣ < δ , δ > 0 } U^{。}=\{ x|\;0<|x-x_0|<\delta,\delta>0 \} U。={x∣0<∣x−x0∣<δ,δ>0}.
2.常见不等式
- 绝对值不等式 − ∣ x ∣ ≤ x ≤ ∣ x ∣ , 0 ≤ x + ∣ x ∣ ≤ 2 ∣ x ∣ , ∀ x ∈ R -|x| \leq x \leq |x|,0\leq x+|x|\leq2|x|,\forall x\in R −∣x∣≤x≤∣x∣,0≤x+∣x∣≤2∣x∣,∀x∈R.
- 三角不等式 ∣ x + y ∣ ≤ ∣ x ∣ + ∣ y ∣ , ∣ ∣ x ∣ − ∣ y ∣ ∣ ≤ ∣ x − y ∣ , ∀ x , y ∈ R |x+y|\leq |x|+|y|,||x|-|y||\leq |x-y|,\forall x,y\in R ∣x+y∣≤∣x∣+∣y∣,∣∣x∣−∣y∣∣≤∣x−y∣,∀x,y∈R.
- 平均值不等式 x 2 + y 2 ≥ 2 x y , ∀ x , y ∈ R x^2+y^2\geq 2xy,\forall x,y\in R x2+y2≥2xy,∀x,y∈R,特别地当 x , y ≥ 时, x + y 2 ≥ x y x,y\geq 时,\frac{x+y}{2}\geq \sqrt{xy} x,y≥时,2x+y≥xy.
- s i n x ≤ x ≤ t a n x , x ∈ [ 0 , π 2 ) sinx\leq x\leq tanx,x\in[0,\frac{π}{2}) sinx≤x≤tanx,x∈[0,2π),等号仅在 x = 0 x=0 x=0时成立。
3.基本初等函数
-
常数函数 y = C y=C y=C,C为常数;
-
幂函数 y = x a , a ∈ R y=x^{a},a\in R y=xa,a∈R;
-
指数函数 y = a x , ( a > 0 , a ≠ 1 ) y=a^{x},(a>0,a\neq 1) y=ax,(a>0,a=1);
-
对数函数 y = log a x , ( a > 0 , a ≠ 1 ) y=\log_{a}x,(a>0,a\neq 1) y=logax,(a>0,a=1);
-
三角函数
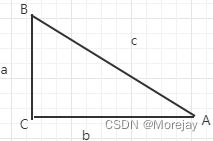
正弦 s i n A = a c 余弦 c o s A = b c 正切 t a n A = a b 余切 c o t A = b a 正割 s e c A = c b 余割 c s c A = c a 其中 c o t A = 1 t a n A s e c A = 1 c o s A c s c A = 1 s i n A 正弦sinA=\frac{a}{c}\qquad余弦cosA=\frac{b}{c}\qquad正切tanA=\frac{a}{b}\\ 余切cotA=\frac{b}{a}\qquad正割secA=\frac{c}{b}\qquad余割cscA=\frac{c}{a}\\ 其中cotA=\frac{1}{tanA}\quad secA=\frac{1}{cosA}\quad cscA=\frac{1}{sinA} 正弦sinA=ca余弦cosA=cb正切tanA=ba余切cotA=ab正割secA=bc余割cscA=ac其中cotA=tanA1secA=cosA1cscA=sinA1 -
反三角函数
a r c s i n x + a r c c o s x = π 2 a r c t a n x + a r c c o t x = π 2 s i n ( a r c s i n x ) = x , x ∈ [ − 1 , 1 ] a r c s i n ( s i n x ) = x , x ∈ [ − π 2 , π 2 ] arcsinx+arccosx=\frac{π}{2} \qquad arctanx+arccotx=\frac{π}{2}\\ sin(arcsinx)=x,x\in[-1,1] \qquad arcsin(sinx)=x,x\in[-\frac{π}{2},\frac{π}{2}] arcsinx+arccosx=2πarctanx+arccotx=2πsin(arcsinx)=x,x∈[−1,1]arcsin(sinx)=x,x∈[−2π,2π]
4.极坐标(与直角坐标系之间的互相转化)
在平面上取定一个极坐标系,以极轴作为直角坐标系的 x x x轴的正半轴,以 θ = π 2 \theta=\frac{π}{2} θ=2π的射线做 y y y轴的正半轴,以极点为坐标原点建立直角坐标系。
直角坐标方程 极坐标方程 x = a ρ = a c o s θ y = a ρ = a s i n θ x 2 + y 2 = r 2 ρ = r x 2 + y 2 − 2 r x = 0 ρ = 2 r c o s θ x 2 + y 2 − 2 r y = 0 ρ = 2 r s i n θ 直角坐标方程 \qquad 极坐标方程\\ x=a \qquad \qquad \rho=\frac{a}{cos\theta}\\ y=a \qquad \qquad \rho=\frac{a}{sin\theta}\\ x^2+y^2=r^2 \qquad \rho=r\\ x^2+y^2-2rx=0 \qquad \rho=2rcos\theta\\ x^2+y^2-2ry=0 \qquad \rho=2rsin \theta 直角坐标方程极坐标方程x=aρ=cosθay=aρ=sinθax2+y2=r2ρ=rx2+y2−2rx=0ρ=2rcosθx2+y2−2ry=0ρ=2rsinθ
极限与连续
1.函数的几种特性
-
有界性
①“函数 f ( x ) f(x) f(x)在闭区间 [ a , b ] [a,b] [a,b]上连续,则在闭区间上有界”;
②“函数 f ( x ) f(x) f(x)在开区间 ( a , b ) (a,b) (a,b)上连续,且 lim x → a + f ( x ) \underset{x\to a^{+}}{\mathop{\lim }}\,f(x) x→a+limf(x)和 lim x → b − f ( x ) \underset{x\to b^{-}}{\mathop{\lim }}\,f(x) x→b−limf(x)都存在,则在开区间上有界”;
③“函数 f ( x ) f(x) f(x)在有限区间I上可导且导函数有界,则函数在该区间上有界”。
-
单调性 “若函数 f ( x ) f(x) f(x)在某区间上有定义,对于区间上任意两点 x 1 < x 2 x_1<x_2 x1<x2恒有 f ( x 1 ) < f ( x 2 ) f(x_1)<f(x2) f(x1)<f(x2)则称 f ( x ) f(x) f(x)在该区间上单调增加;若恒有 f ( x 1 ) ≥ f ( x 2 ) f(x_1)\geq f(x_2) f(x1)≥f(x2),成 f ( x ) f(x) f(x)在该区间上单调不增”。
-
奇偶性
-
周期性
2.极限
- 数列的极限 “如果对于任意给定的 ϵ > 0 \epsilon>0 ϵ>0,总存在正整数N,当 n > N n>N n>N时,恒有 ∣ x n − a ∣ < ϵ |x_n-a|<\epsilon ∣xn−a∣<ϵ成立,则称常数a为数列 { x n } \{x_n\} {xn}当n趋近于无穷时的极限,记为 lim n → ∞ x n = a \underset{n\to\infty}{\mathop{\lim }}\,x_n = a n→∞limxn=a”。
- 函数的极限 “如果对于任意给定的 ϵ > 0 \epsilon>0 ϵ>0,总存在 X > 0 X>0 X>0,当 ∣ x ∣ > X |x|>X ∣x∣>X时,恒有 ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ成立,则称常数A为函数 f ( x ) f(x) f(x)当x趋近于无穷时的极限,记为 lim x → ∞ f ( x ) = A \underset{x\to\infty}{\mathop{\lim }}\,f(x) = A x→∞limf(x)=A”;“如果对于任意给定的 ϵ > 0 \epsilon>0 ϵ>0,总存在 δ > 0 \delta>0 δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ时,恒有 ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ成立,则称常数A为函数 f ( x ) f(x) f(x)当x趋近于 x 0 x_0 x0的极限,记为 lim x → x 0 f ( x ) = A \underset{x\to x_0}{\mathop{\lim }}\,f(x) = A x→x0limf(x)=A”。
极限的几种特性
-
有界性 “数列收敛 ⇒ \Rightarrow ⇒有界;无界数列必发散,但发散不一定无界;若 lim x → x 0 f ( x ) \lim_{x\rightarrow x_0}\;f(x) limx→x0f(x)存在,则 f ( x ) f(x) f(x)在 x 0 x_0 x0某去心邻域有界(局部有界)”
-
保号性
极限存在判定
- 夹逼准则
- 单调有界准则
无穷大与无穷小
有限个无穷小的和(积)仍为无穷小
当 x → + ∞ x\rightarrow +\infty x→+∞时, ln α x < < x β < < a x \ln^{\alpha}x\;<<\;x^{\beta}\;<<\;a^{x} lnαx<<xβ<<ax,其中 α > 0 , β > 0 , a > 1 \alpha>0,\beta>0,a>1 α>0,β>0,a>1。
两个重要极限
lim x → 0 s i n x x = 1 lim x → ∞ ( 1 + 1 x ) x = e \lim_{x\rightarrow 0}\,\frac{sinx}{x}=1\qquad\lim_{x\rightarrow\infty}(1+\frac{1}{x})^{x}=e x→0limxsinx=1x→∞lim(1+x1)x=e
一元函数微积分学
1.导数
倒数定义
f ′ ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'({{x}_{0}})=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{\Delta x} f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)
或者:
f ′ ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'({{x}_{0}})=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f(x)-f({{x}_{0}})}{x-{{x}_{0}}} f′(x0)=x→x0limx−x0f(x)−f(x0)。
导数的几何意义
“ f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处的导数 f ′ ( x 0 ) f^{'}(x_0) f′(x0)是曲线 y = f ( x ) y=f(x) y=f(x)在点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))处的切线斜率”;
“ y = f ( x ) y=f(x) y=f(x)在 x = x 0 x=x_0 x=x0处可导 ⇔ f ( x ) \Leftrightarrow f(x) ⇔f(x)在 x = x 0 x=x_0 x=x0处可微”。
左右导数导数
左导数: f ′ − ( x 0 ) = lim Δ x → 0 − f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 , ( x = x 0 + Δ x ) {{{f}'}_{-}}({{x}_{0}})=\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{\Delta x}=\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,\frac{f(x)-f({{x}_{0}})}{x-{{x}_{0}}},(x={{x}_{0}}+\Delta x) f′−(x0)=Δx→0−limΔxf(x0+Δx)−f(x0)=x→x0−limx−x0f(x)−f(x0),(x=x0+Δx)
右导数: f ′ + ( x 0 ) = lim Δ x → 0 + f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 {{{f}'}_{+}}({{x}_{0}})=\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{\Delta x}=\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,\frac{f(x)-f({{x}_{0}})}{x-{{x}_{0}}} f′+(x0)=Δx→0+limΔxf(x0+Δx)−f(x0)=x→x0+limx−x0f(x)−f(x0)
“若函数在点 x 0 x_0 x0处可导,则 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0处连续,反之则不成立。即函数连续不一定可导,但可导必连续。”
f ′ ( x 0 ) {f}'({{x}_{0}}) f′(x0)存在 ⇔ f ′ − ( x 0 ) = f ′ + ( x 0 ) \Leftrightarrow {{{f}'}_{-}}({{x}_{0}})={{{f}'}_{+}}({{x}_{0}}) ⇔f′−(x0)=f′+(x0)。
求导(微分)运算法则
设函数 u = u ( x ) , v = v ( x ) u=u(x),v=v(x) u=u(x),v=v(x)在点 x x x可导则
(1) ( u ± v ) ′ = u ′ ± v ′ (u\pm v{)}'={u}'\pm {v}' (u±v)′=u′±v′ d ( u ± v ) = d u ± d v d(u\pm v)=du\pm dv d(u±v)=du±dv
(2) ( u v ) ′ = u v ′ + v u ′ (uv{)}'=u{v}'+v{u}' (uv)′=uv′+vu′ d ( u v ) = u d v + v d u d(uv)=udv+vdu d(uv)=udv+vdu
(3) ( u v ) ′ = v u ′ − u v ′ v 2 ( v ≠ 0 ) (\frac{u}{v}{)}'=\frac{v{u}'-u{v}'}{{{v}^{2}}}(v\ne 0) (vu)′=v2vu′−uv′(v=0) d ( u v ) = v d u − u d v v 2 d(\frac{u}{v})=\frac{vdu-udv}{{{v}^{2}}} d(vu)=v2vdu−udv
(4)链式法则:设 y = f ( u ) , u = ϕ ( x ) y=f(u),u=\phi(x) y=f(u),u=ϕ(x)则有 d y d x = d y d u ⋅ d u d x \frac{dy}{dx}=\frac{dy}{du}·\frac{du}{dx} dxdy=dudy⋅dxdu
基本导数与微分表
(1) y = c y=c y=c(常数) y ′ = 0 {y}'=0 y′=0 d y = 0 dy=0 dy=0
(2) y = x α y={{x}^{\alpha }} y=xα( α \alpha α为实数) y ′ = α x α − 1 {y}'=\alpha {{x}^{\alpha -1}} y′=αxα−1 d y = α x α − 1 d x dy=\alpha {{x}^{\alpha -1}}dx dy=αxα−1dx
(3) y = a x y={{a}^{x}} y=ax y ′ = a x ln a {y}'={{a}^{x}}\ln a y′=axlna d y = a x ln a d x dy={{a}^{x}}\ln adx dy=axlnadx
特例: ( e x ) ′ = e x ({{{e}}^{x}}{)}'={{{e}}^{x}} (ex)′=ex d ( e x ) = e x d x d({{{e}}^{x}})={{{e}}^{x}}dx d(ex)=exdx
(4) y = log a x y={{\log }_{a}}x y=logax y ′ = 1 x ln a {y}'=\frac{1}{x\ln a} y′=xlna1
d y = 1 x ln a d x dy=\frac{1}{x\ln a}dx dy=xlna1dx
特例: y = ln x y=\ln x y=lnx ( ln x ) ′ = 1 x (\ln x{)}'=\frac{1}{x} (lnx)′=x1 d ( ln x ) = 1 x d x d(\ln x)=\frac{1}{x}dx d(lnx)=x1dx
(5) y = sin x y=\sin x y=sinx y ′ = cos x {y}'=\cos x y′=cosx d ( sin x ) = cos x d x d(\sin x)=\cos xdx d(sinx)=cosxdx
(6) y = cos x y=\cos x y=cosx y ′ = − sin x {y}'=-\sin x y′=−sinx d ( cos x ) = − sin x d x d(\cos x)=-\sin xdx d(cosx)=−sinxdx
(7) y = tan x y=\tan x y=tanx y ′ = 1 cos 2 x = sec 2 x {y}'=\frac{1}{{{\cos }^{2}}x}={{\sec }^{2}}x y′=cos2x1=sec2x d ( tan x ) = sec 2 x d x d(\tan x)={{\sec }^{2}}xdx d(tanx)=sec2xdx
(8) y = cot x y=\cot x y=cotx y ′ = − 1 sin 2 x = − csc 2 x {y}'=-\frac{1}{{{\sin }^{2}}x}=-{{\csc }^{2}}x y′=−sin2x1=−csc2x d ( cot x ) = − csc 2 x d x d(\cot x)=-{{\csc }^{2}}xdx d(cotx)=−csc2xdx
(9) y = sec x y=\sec x y=secx y ′ = sec x tan x {y}'=\sec x\tan x y′=secxtanx d ( sec x ) = sec x tan x d x d(\sec x)=\sec x\tan xdx d(secx)=secxtanxdx
(10) y = csc x y=\csc x y=cscx y ′ = − csc x cot x {y}'=-\csc x\cot x y′=−cscxcotx d ( csc x ) = − csc x cot x d x d(\csc x)=-\csc x\cot xdx d(cscx)=−cscxcotxdx
(11) y = arcsin x y=\arcsin x y=arcsinx y ′ = 1 1 − x 2 {y}'=\frac{1}{\sqrt{1-{{x}^{2}}}} y′=1−x21 d ( arcsin x ) = 1 1 − x 2 d x d(\arcsin x)=\frac{1}{\sqrt{1-{{x}^{2}}}}dx d(arcsinx)=1−x21dx
(12) y = arccos x y=\arccos x y=arccosx y ′ = − 1 1 − x 2 {y}'=-\frac{1}{\sqrt{1-{{x}^{2}}}} y′=−1−x21 d ( arccos x ) = − 1 1 − x 2 d x d(\arccos x)=-\frac{1}{\sqrt{1-{{x}^{2}}}}dx d(arccosx)=−1−x21dx
(13) y = arctan x y=\arctan x y=arctanx y ′ = 1 1 + x 2 {y}'=\frac{1}{1+{{x}^{2}}} y′=1+x21 d ( arctan x ) = 1 1 + x 2 d x d(\arctan x)=\frac{1}{1+{{x}^{2}}}dx d(arctanx)=1+x21dx
(14) y = arc cot x y=\operatorname{arc}\cot x y=arccotx y ′ = − 1 1 + x 2 {y}'=-\frac{1}{1+{{x}^{2}}} y′=−1+x21 d ( arc cot x ) = − 1 1 + x 2 d x d(\operatorname{arc}\cot x)=-\frac{1}{1+{{x}^{2}}}dx d(arccotx)=−1+x21dx
复合、反、隐函数以及参数方程的微分
(1) 反函数的运算法则: 设 y = f ( x ) y=f(x) y=f(x)在点 x x x的某邻域内单调连续,在点 x x x处可导且 f ′ ( x ) ≠ 0 {f}'(x)\ne 0 f′(x)=0,则其反函数在点 x x x所对应的 y y y处可导,并且有 d y d x = 1 d x d y \frac{dy}{dx}=\frac{1}{\frac{dx}{dy}} dxdy=dydx1
(2) 复合函数的运算法则:若 μ = φ ( x ) \mu =\varphi(x) μ=φ(x) 在点 x x x可导,而 y = f ( μ ) y=f(\mu) y=f(μ)在对应点 μ \mu μ( μ = φ ( x ) \mu =\varphi (x) μ=φ(x))可导,则复合函数 y = f ( φ ( x ) ) y=f(\varphi (x)) y=f(φ(x))在点 x x x可导,且 y ′ = f ′ ( μ ) ⋅ φ ′ ( x ) {y}'={f}'(\mu )\cdot {\varphi }'(x) y′=f′(μ)⋅φ′(x)
(3) 隐函数导数 d y d x \frac{dy}{dx} dxdy的求法一般有三种方法:
1)方程两边对 x x x求导,要记住 y y y是 x x x的函数,则 y y y的函数是 x x x的复合函数.例如 1 y \frac{1}{y} y1, y 2 {{y}^{2}} y2, l n y ln y lny, e y {{{e}}^{y}} ey等均是 x x x的复合函数.
对 x x x求导应按复合函数链式法则做.
2)公式法.由 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0知 d y d x = − F ′ x ( x , y ) F ′ y ( x , y ) \frac{dy}{dx}=-\frac{{{{{F}'}}_{x}}(x,y)}{{{{{F}'}}_{y}}(x,y)} dxdy=−F′y(x,y)F′x(x,y),其中, F ′ x ( x , y ) {{{F}'}_{x}}(x,y) F′x(x,y),
F ′ y ( x , y ) {{{F}'}_{y}}(x,y) F′y(x,y)分别表示 F ( x , y ) F(x,y) F(x,y)对 x x x和 y y y的偏导数
3)利用微分形式不变性
常用高阶导数公式
(1) ( a x ) ( n ) = a x ln n a ( a > 0 ) ( e x ) ( n ) = e x ({{a}^{x}}){{\,}^{(n)}}={{a}^{x}}{{\ln }^{n}}a\quad (a>{0})\quad \quad ({{{e}}^{x}}){{\,}^{(n)}}={e}{{\,}^{x}} (ax)(n)=axlnna(a>0)(ex)(n)=ex
(2) ( sin k x ) ( n ) = k n sin ( k x + n ⋅ π 2 ) (\sin kx{)}{{\,}^{(n)}}={{k}^{n}}\sin (kx+n\cdot \frac{\pi }{{2}}) (sinkx)(n)=knsin(kx+n⋅2π)
(3) ( cos k x ) ( n ) = k n cos ( k x + n ⋅ π 2 ) (\cos kx{)}{{\,}^{(n)}}={{k}^{n}}\cos (kx+n\cdot \frac{\pi }{{2}}) (coskx)(n)=kncos(kx+n⋅2π)
(4) ( x m ) ( n ) = m ( m − 1 ) ⋯ ( m − n + 1 ) x m − n ({{x}^{m}}){{\,}^{(n)}}=m(m-1)\cdots (m-n+1){{x}^{m-n}} (xm)(n)=m(m−1)⋯(m−n+1)xm−n
(5) ( ln x ) ( n ) = ( − 1 ) ( n − 1 ) ( n − 1 ) ! x n (\ln x){{\,}^{(n)}}={{(-{1})}^{(n-{1})}}\frac{(n-{1})!}{{{x}^{n}}} (lnx)(n)=(−1)(n−1)xn(n−1)!
(6)莱布尼兹公式:若 u ( x ) , v ( x ) u(x)\,,v(x) u(x),v(x)均 n n n阶可导,则
( u v ) ( n ) = ∑ i = 0 n c n i u ( i ) v ( n − i ) {{(uv)}^{(n)}}=\sum\limits_{i={0}}^{n}{c_{n}^{i}{{u}^{(i)}}{{v}^{(n-i)}}} (uv)(n)=i=0∑ncniu(i)v(n−i),其中 u ( 0 ) = u {{u}^{({0})}}=u u(0)=u, v ( 0 ) = v {{v}^{({0})}}=v v(0)=v.
2.导数的应用
- 极值点
- 单调性的判定
- 曲线的凹凸性和拐点
- 曲线渐近线(水平、铅直和斜)
- 曲率、曲率圆与曲率半径 “ k = ∣ y " ∣ ( 1 + y ′ 2 ) 3 / 2 k=\frac{|y^{"}|}{(1+y^{'2})^{3/2}} k=(1+y′2)3/2∣y"∣, R = 1 k R=\frac{1}{k} R=k1”
3.中值定理
Th1:(费马定理)
若函数 f ( x ) f(x) f(x)在 x 0 {{x}_{0}} x0的某邻域内有定义,并且在此邻域内恒有 f ( x ) ≤ f ( x 0 ) f(x)\le f({{x}_{0}}) f(x)≤f(x0)或 f ( x ) ≥ f ( x 0 ) f(x)\ge f({{x}_{0}}) f(x)≥f(x0),又设 f ( x ) f(x) f(x)在 x 0 {{x}_{0}} x0处可导,则有 f ′ ( x 0 ) = 0 {f}'({{x}_{0}})=0 f′(x0)=0。
Th2:(罗尔定理)
设函数 f ( x ) f(x) f(x)满足条件:
- 在闭区间 [ a , b ] [a,b] [a,b]上连续,在 ( a , b ) (a,b) (a,b)内可导;
- f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b);
则在 ( a , b ) (a,b) (a,b)内一存在个 ξ \xi ξ,使 f ′ ( ξ ) = 0 {f}'(\xi )=0 f′(ξ)=0
Th3: (拉格朗日中值定理)
设函数 f ( x ) f(x) f(x)满足条件:
- 在 [ a , b ] [a,b] [a,b]上连续,在 ( a , b ) (a,b) (a,b)内可导;
则在 ( a , b ) (a,b) (a,b)内一存在个 ξ \xi ξ,使 f ( b ) − f ( a ) b − a = f ′ ( ξ ) \frac{f(b)-f(a)}{b-a}={f}'(\xi ) b−af(b)−f(a)=f′(ξ)
Th4: (柯西中值定理)
设函数 f ( x ) f(x) f(x), g ( x ) g(x) g(x)满足条件:
- 在 [ a , b ] [a,b] [a,b]上连续,在 ( a , b ) (a,b) (a,b)内可导
- f ′ ( x ) {f}'(x) f′(x), g ′ ( x ) {g}'(x) g′(x)均存在,且 g ′ ( x ) ≠ 0 {g}'(x)\ne 0 g′(x)=0
则在 ( a , b ) (a,b) (a,b)内存在一个 ξ \xi ξ,使 f ( b ) − f ( a ) g ( b ) − g ( a ) = f ′ ( ξ ) g ′ ( ξ ) \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{{f}'(\xi )}{{g}'(\xi )} g(b)−g(a)f(b)−f(a)=g′(ξ)f′(ξ)。
应用
- 不等式的证明
- 零点问题
4.泰勒公式
设函数 f ( x ) f(x) f(x)在点 x 0 {{x}_{0}} x0处的某邻域内具有 n + 1 n+1 n+1阶导数,则对该邻域内异于 x 0 {{x}_{0}} x0的任意点 x x x,在 x 0 {{x}_{0}} x0与 x x x之间至少存在一个 ξ \xi ξ,使得:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 ! f ′ ′ ( x 0 ) ( x − x 0 ) 2 + ⋯ f(x)=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}})+\frac{1}{2!}{f}''({{x}_{0}}){{(x-{{x}_{0}})}^{2}}+\cdots f(x)=f(x0)+f′(x0)(x−x0)+2!1f′′(x0)(x−x0)2+⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) +\frac{{{f}^{(n)}}({{x}_{0}})}{n!}{{(x-{{x}_{0}})}^{n}}+{{R}_{n}}(x) +n!f(n)(x0)(x−x0)n+Rn(x)
其中 R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 {{R}_{n}}(x)=\frac{{{f}^{(n+1)}}(\xi )}{(n+1)!}{{(x-{{x}_{0}})}^{n+1}} Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1称为 f ( x ) f(x) f(x)在点 x 0 {{x}_{0}} x0处的 n n n阶拉格朗日余项。
令 x 0 = 0 {{x}_{0}}=0 x0=0,则 n n n阶泰勒公式
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + 1 2 ! f ′ ′ ( 0 ) x 2 + ⋯ + f ( n ) ( 0 ) n ! x n + R n ( x ) f(x)=f(0)+{f}'(0)x+\frac{1}{2!}{f}''(0){{x}^{2}}+\cdots +\frac{{{f}^{(n)}}(0)}{n!}{{x}^{n}}+{{R}_{n}}(x) f(x)=f(0)+f′(0)x+2!1f′′(0)x2+⋯+n!f(n)(0)xn+Rn(x)
其中 R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! x n + 1 {{R}_{n}}(x)=\frac{{{f}^{(n+1)}}(\xi )}{(n+1)!}{{x}^{n+1}} Rn(x)=(n+1)!f(n+1)(ξ)xn+1, ξ \xi ξ在0与 x x x之间,上式称为麦克劳林公式
常用五种函数在 x 0 = 0 {{x}_{0}}=0 x0=0处的泰勒公式
(1) e x = 1 + x + 1 2 ! x 2 + ⋯ + 1 n ! x n + x n + 1 ( n + 1 ) ! e ξ {{{e}}^{x}}=1+x+\frac{1}{2!}{{x}^{2}}+\cdots +\frac{1}{n!}{{x}^{n}}+\frac{{{x}^{n+1}}}{(n+1)!}{{e}^{\xi }} ex=1+x+2!1x2+⋯+n!1xn+(n+1)!xn+1eξ
或 = 1 + x + 1 2 ! x 2 + ⋯ + 1 n ! x n + o ( x n ) =1+x+\frac{1}{2!}{{x}^{2}}+\cdots +\frac{1}{n!}{{x}^{n}}+o({{x}^{n}}) =1+x+2!1x2+⋯+n!1xn+o(xn)(佩亚诺余项)
(2) sin x = x − 1 3 ! x 3 + ⋯ + x n n ! sin n π 2 + x n + 1 ( n + 1 ) ! sin ( ξ + n + 1 2 π ) \sin x=x-\frac{1}{3!}{{x}^{3}}+\cdots +\frac{{{x}^{n}}}{n!}\sin \frac{n\pi }{2}+\frac{{{x}^{n+1}}}{(n+1)!}\sin (\xi +\frac{n+1}{2}\pi ) sinx=x−3!1x3+⋯+n!xnsin2nπ+(n+1)!xn+1sin(ξ+2n+1π)
或 = x − 1 3 ! x 3 + ⋯ + x n n ! sin n π 2 + o ( x n ) =x-\frac{1}{3!}{{x}^{3}}+\cdots +\frac{{{x}^{n}}}{n!}\sin \frac{n\pi }{2}+o({{x}^{n}}) =x−3!1x3+⋯+n!xnsin2nπ+o(xn)
(3) cos x = 1 − 1 2 ! x 2 + ⋯ + x n n ! cos n π 2 + x n + 1 ( n + 1 ) ! cos ( ξ + n + 1 2 π ) \cos x=1-\frac{1}{2!}{{x}^{2}}+\cdots +\frac{{{x}^{n}}}{n!}\cos \frac{n\pi }{2}+\frac{{{x}^{n+1}}}{(n+1)!}\cos (\xi +\frac{n+1}{2}\pi ) cosx=1−2!1x2+⋯+n!xncos2nπ+(n+1)!xn+1cos(ξ+2n+1π)
或 = 1 − 1 2 ! x 2 + ⋯ + x n n ! cos n π 2 + o ( x n ) =1-\frac{1}{2!}{{x}^{2}}+\cdots +\frac{{{x}^{n}}}{n!}\cos \frac{n\pi }{2}+o({{x}^{n}}) =1−2!1x2+⋯+n!xncos2nπ+o(xn)
(4) ln ( 1 + x ) = x − 1 2 x 2 + 1 3 x 3 − ⋯ + ( − 1 ) n − 1 x n n + ( − 1 ) n x n + 1 ( n + 1 ) ( 1 + ξ ) n + 1 \ln (1+x)=x-\frac{1}{2}{{x}^{2}}+\frac{1}{3}{{x}^{3}}-\cdots +{{(-1)}^{n-1}}\frac{{{x}^{n}}}{n}+\frac{{{(-1)}^{n}}{{x}^{n+1}}}{(n+1){{(1+\xi )}^{n+1}}} ln(1+x)=x−21x2+31x3−⋯+(−1)n−1nxn+(n+1)(1+ξ)n+1(−1)nxn+1
或 = x − 1 2 x 2 + 1 3 x 3 − ⋯ + ( − 1 ) n − 1 x n n + o ( x n ) =x-\frac{1}{2}{{x}^{2}}+\frac{1}{3}{{x}^{3}}-\cdots +{{(-1)}^{n-1}}\frac{{{x}^{n}}}{n}+o({{x}^{n}}) =x−21x2+31x3−⋯+(−1)n−1nxn+o(xn)
(5) ( 1 + x ) m = 1 + m x + m ( m − 1 ) 2 ! x 2 + ⋯ + m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n {{(1+x)}^{m}}=1+mx+\frac{m(m-1)}{2!}{{x}^{2}}+\cdots +\frac{m(m-1)\cdots (m-n+1)}{n!}{{x}^{n}} (1+x)m=1+mx+2!m(m−1)x2+⋯+n!m(m−1)⋯(m−n+1)xn
+ m ( m − 1 ) ⋯ ( m − n + 1 ) ( n + 1 ) ! x n + 1 ( 1 + ξ ) m − n − 1 +\frac{m(m-1)\cdots (m-n+1)}{(n+1)!}{{x}^{n+1}}{{(1+\xi )}^{m-n-1}} +(n+1)!m(m−1)⋯(m−n+1)xn+1(1+ξ)m−n−1
或 ( 1 + x ) m = 1 + m x + m ( m − 1 ) 2 ! x 2 + ⋯ {{(1+x)}^{m}}=1+mx+\frac{m(m-1)}{2!}{{x}^{2}}+\cdots (1+x)m=1+mx+2!m(m−1)x2+⋯ , + m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n + o ( x n ) +\frac{m(m-1)\cdots (m-n+1)}{n!}{{x}^{n}}+o({{x}^{n}}) +n!m(m−1)⋯(m−n+1)xn+o(xn)
(6) 1 1 − x = 1 + x + x 2 + x 3 + o ( x 3 ) \frac{1}{1-x}=1+x+x^2+x^3+o(x^3) 1−x1=1+x+x2+x3+o(x3)
(7) t a n x = x + x 3 3 + o ( x 3 ) tanx=x+\frac{x^3}{3}+o(x^3) tanx=x+3x3+o(x3)
5.不定积分与定积分
原函数与不定积分 “设 F ′ ( x ) = f ( x ) , x ∈ ( a , b ) F'(x)=f(x),x\in(a,b) F′(x)=f(x),x∈(a,b),则称 F ( x ) F(x) F(x)为 f ( x ) f(x) f(x)在区间 ( a , b ) (a,b) (a,b)上的一个原函数,记为 ∫ f ( x ) d x = F ( x ) + C \int f(x)dx=F(x)+C ∫f(x)dx=F(x)+C,其中C为任意常数”
定积分存在定理
- 设 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上连续,则 ∫ a b f ( x ) d x \int_a^bf(x)dx ∫abf(x)dx存在(原函数存在).
- 设 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上有界,且只有有限个间断点,则 ∫ a b f ( x ) d x \int_a^bf(x)dx ∫abf(x)dx存在.
反常积分
设 f ( x ) f(x) f(x)在 [ a , + ∞ ] [a,+\infty] [a,+∞]上连续,称 ∫ a + ∞ f ( x ) d x = lim b → + ∞ ∫ a b f ( x ) d x \int_a^{+\infty}f(x)dx=\lim_{b\rightarrow+\infty}\int_a^bf(x)dx ∫a+∞f(x)dx=limb→+∞∫abf(x)dx为 f ( x ) f(x) f(x)在 [ a , + ∞ ] [a,+\infty] [a,+∞]上的反常积分。若右边极限存在,称此反常积分收敛;否则此反常积分发散。
重要反常积分: ∫ − ∞ + ∞ e − x 2 d x = 2 ∫ 0 + ∞ e − x 2 d x = π \int_{-\infty}^{+\infty}e^{-x^2}dx=2\int_{0}^{+\infty}e^{-x^2}dx=\sqrt{π} ∫−∞+∞e−x2dx=2∫0+∞e−x2dx=π
定积分的应用
- 平面图形面积 “极坐标曲线 r = r ( θ ) r=r(\theta) r=r(θ)介于两射线 θ = α \theta=\alpha θ=α与 θ = β ( 0 < β − α ≤ 2 π ) \theta=\beta\quad(0<\beta-\alpha\le2π) θ=β(0<β−α≤2π)之间的曲边扇形面积 A = 1 2 ∫ α β r 2 ( θ ) d θ A=\frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)d\theta A=21∫αβr2(θ)dθ”
- 平面曲线的弧长 “直角坐标 s = ∫ a b 1 + y ′ 2 ( x ) d x s=\int_a^b\sqrt{1+y'^{2}(x)}dx s=∫ab1+y′2(x)dx;极坐标 s = ∫ α β r 2 ( θ ) + r ′ 2 ( θ ) d θ s=\int_{\alpha}^{\beta}\sqrt{r^2(\theta)+r'^{2}(\theta)}d\theta s=∫αβr2(θ)+r′2(θ)dθ”
- 旋转体体积 “曲线 y = f ( x ) y=f(x) y=f(x)与 x = a , x = b , x x=a,x=b,x x=a,x=b,x轴围成的曲边梯形绕 x x x轴旋转一周 V = π ∫ a b y 2 ( x ) d x , a < b V=\pi\int_a^by^2(x)dx,a<b V=π∫aby2(x)dx,a<b;绕 y y y轴旋转一周 V = 2 π ∫ a b x y ( x ) d x V=2\pi\int_a^bxy(x)dx V=2π∫abxy(x)dx”
- 旋转曲面面积
- 函数平均值 f ‾ = 1 b − a ∫ a b f ( x ) d x \overline{f}=\frac{1}{b-a}\int_a^bf(x)dx f=b−a1∫abf(x)dx.
多元函数微积分学
二元函数连续是在一元函数基础上的推论
二元函数的偏导数与全微分
二重极限的存在性
二元函数的可微性
复合函数的偏导数与全微分
多元函数的极值与最值
- 无条件极值
若存在 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)点的某邻域 U δ ( M 0 ) U_\delta(M_0) Uδ(M0),使得 f ( x , y ) ≤ ( 或 ≥ ) f ( x 0 , y 0 ) , ∀ ( x , y ) ∈ U δ ( M 0 ) f(x,y)\le(或\ge)f(x_0,y_0),\forall(x,y)\in U_\delta(M_0) f(x,y)≤(或≥)f(x0,y0),∀(x,y)∈Uδ(M0),则称 f ( x , y ) f(x,y) f(x,y)在点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)处取得极小(大)值。
凡是能使 f x ′ ( x , y ) = 0 , f y ′ ( x , y ) = 0 f'_x(x,y)=0,f'_y(x,y)=0 fx′(x,y)=0,fy′(x,y)=0同时成立的点称为二元函数的驻点,但驻点不等价于极值点。
具有一阶偏导数的函数的极值点一定是驻点,但驻点不一定是极值点。
- 条件极值
函数 f ( x , y ) f(x,y) f(x,y)在条件 ϕ ( x , y ) = 0 \phi(x,y)=0 ϕ(x,y)=0下的极值,先构造拉格朗日(辅助)函数 F ( x , y , λ ) = f ( x , y ) + λ ϕ ( x , y ) F(x,y,\lambda)=f(x,y)+\lambda\phi(x,y) F(x,y,λ)=f(x,y)+λϕ(x,y).
二重积分
常微分方程
含有未知函数,未知函数的导数与自变量之间关系的方程,叫做微分方程。
- 可分离变量的方程
- 齐次方程
- 线性方程
- 可降价的高阶微分方程
这篇关于深度学习需要掌握的数学知识①【高等数学】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





