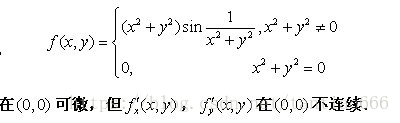高等数学专题
【高等数学学习记录】映射
【高等数学&学习记录】映射 从事测绘工作多年,深刻感受到基础知识的重要及自身在这方面的短板。 为此,打算重温测绘工作所需基础知识。练好基本功,为测绘工作赋能。 1 知识点 1.1 映射 映射 设 X X X、 Y Y Y是非空集合,若存在法则 f f f,使 X X X中每个元素 x x x,在 Y Y Y中有唯一确定的元素 y y y与之对应,则称 f f f为从 X X X到
【高等数学】【综合习题】第一章:函数、极限与函数连续性
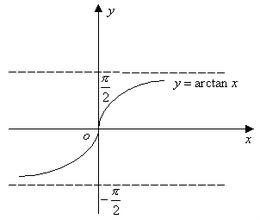
文章目录 一. 选择二. 填空题1. 泰勒公式2. 积分与极限 三. 大题 一. 选择 x p {x^p} xp 放到一起求极限 正常思路求解:求积分即可。 带入求导:题型不具备典型性。 直接按照求导公式 有界性arctanx的函数图像。 函数图像与极限的结合 取特殊值 夹逼
考研数学 高等数学----导数应用
核心框架 前置知识 正式内容 知识点1: 知识点2: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识
高等数学精解【11】
文章目录 抛物线基础抛物线的方程1. 标准形式2. 顶点形式3. 焦点形式4. 一般形式示例 抛物线的应用1. 图像处理2. 目标检测与识别3. 路径预测4. 特定场景下的应用5. 算法优化与计算 自适应抛物线算法(Adaptive Parabola Algorithm)原理一、原理二、计算三、例子四、例题 自适应抛物线算法过程一、原理二、计算过程三、例子四、例题(假设性) 抛物线滤波器(P
【高等数学】傅里叶级数
最近刷了会抖音,看到一个非常有趣的现象:傅里叶级数,今天挑了几个视频来供大家学习。 1.傅里叶级数概念 【小崔说数】傅里叶级数专题https://www.bilibili.com/video/BV1Uq4y1q7xk?t=117.4 2.傅里叶级数动画 【谜之舒适】12分钟的傅立叶级数动画https://www.bilibili.com/video/BV1o4411D7vm?t=355.8
高等数学笔记(三):导数
一、导数概念 1.1 导数的定义 1.1.1 函数在一点处的导数与导函数 1.1.2 单侧导数 1.2 导数的几何意义 1.3 函数可导性与连续性的关系 二、函数的求导法则 2.1 函数的和、差、积、商的求导法则 2.2 反函数的求导法则 2.3 复合函数的求导法则 2.4 基本求导法则与导数公式 三、高阶导数 四、隐函数及由参数
高等数学笔记(二):极限
一、数列极限的定义 以下符号表示 “对于任意给定的” 以下符号表示 “存在” 以下符号表示 “如果什么(箭头左),则什么(箭头右)” 二、收敛数列的性质 2.1 唯一性 2.2 有界性 2.3 保号性 2.4 子数列收敛性 三、函数极限的定义 3.1 自变量趋于有限值时函数的极限 这里画图的话简单明了,上面的绝对值表示距离 3
掌握高等数学、线性代数、概率论所需数学知识及标题建议
在数学的广袤领域中,高等数学、线性代数和概率论作为三大核心分支,不仅在理论研究中占据重要地位,更在实际应用中发挥着举足轻重的作用。为了深入理解和掌握这三门学科,我们需要掌握一系列扎实的数学知识。 高等数学所需数学知识 高等数学是大学数学的重要组成部分,它以微积分为主要内容,研究函数、极限、导数、微分、积分等概念和方法。要学好高等数学,需要掌握以下数学知识: 基本代数知识:包括多项式的加减
【高等数学】向量代数
向量代数 1、向量的概念及其线性运算1.1、向量的概念1.2、向量的线性运算1.2.1、向量的加法1.2.2、向量的减法1.2.3、向量与数的乘法 1.3、空间直角坐标系1.3.1、空间直角坐标系的基本概念1.3.2、向量的坐标表示 1.4、利用坐标作向量的线性运算1.5、向量的模、方向角、投影1.5.1、向量的模与两点间距离公式1.5.2、方向角与方向余弦1.5.3、向量在轴上的投影 2
高等数学基础篇之导数与微分的运算法则
导数与微分: 一、导数基本公式 二、微分基本公式 三、导数运算法则 四、微分运算法则 一、导数基本公式 二、微分基本公式 三、导数运算法则 四、微分运算法则 有理运算法则 设f(x), g(x)在x处可导,则: 复合函数运算法则 设 y=f(u)
概率论考点之估计量(高等数学求最值)
如题:2019年10月 分析:新东西…………。大体看了下,应该是属于统计量及其分布的内容。 答案:根据《概率论复习之关于点估计》问题3中无偏性,样本k阶原点矩是总体k阶原点矩的无偏估计,原点矩的表达式为C 1、什么是统计量呢???? 用样本来表达的一个量,并且没有未知参数。如下定义:至于什么是样本?,详见扩展1: 2、什么又是无偏差????首先搞明白什么是偏差??详见扩展2
高等数学一——微积分个人笔记
该博客记录一些细点。 1.数列存在极限数列,但函数不存在极限函数,因为函数存在无数种趋近情况: 例如对于f(x)=x,不存在极限;而因此不能简单地讨论函数是否有极限。 而数组有确定的下标值,对于其中地某一个数组下标,都有确切的值与它对应,只有数组单方向无限延申的时候才有无限趋近的可能。 2.对于,函数剧烈波动。
高等数学——求解不定积分的经典换元法
本文始发于个人公众号:TechFlow,原创不易,求个关注 今天是高等数学专题的第九篇文章,我们继续来看不定积分。 在上篇文章当中我们回顾了不定积分的定义以及简单的性质,我们可以简单地认为不定积分就是求导微分的逆操作。我们要做的是根据现有的导函数,逆推出求导之前的原函数。 除了基本定义之外,我们还介绍了一些简单的性质和常用积分的积分表。但是显然根据已有的性质对于许多复杂的函数来说求解积分
高等数学——微积分中的不定积分
本文始发于个人公众号:TechFlow,原创不易,求个关注 今天是高等数学专题的第8篇文章,今天的内容是不定积分。 我之前的高数老师曾经说过,高等数学就是大半本的微积分加上一些数列和极限的知识。而微积分当中,积分相关又占据了大半江山。微积分之所以重要并不是因为它的比重大、容量多,而是因为它常用。几乎所有理工科的课本上都有微积分的公式,原因也很简单,当年这些科学家在研究未知事物或者是进行计算
高等数学——手撕牛顿莱布尼茨公式
本文始发于个人公众号:TechFlow,原创不易,求个关注 今天是高等数学专题的第13篇文章,我们来看看定积分究竟应该怎么计算。 定积分的实际意义 通过之前的文章,我们基本上熟悉了定积分这个概念和它的一些简单性质,今天终于到了正题,我们要试着来算一算这个积分了。 我们先来回忆一下对定积分的直观感受,它可以代表一段曲形面积,比如: 如果我们把上图当中的f(x)看成是速度函数
考研数学二复习笔记-高等数学-第二章 一元函数微分学
1.导数和微分 求导 使用导数的定义 f ′ ( x ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 或者 f ′ ( x ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x)=\lim_{x \to{x0}}\frac{f(x)-f(x0)}{x-x0} 或者f'(x)=\lim_{
【考研数学】高等数学总结
文章目录 第一章 极限 函数 连续1.1 极限存在准则及两个重要极限1.1.1 夹逼定理1.1.1.1 数列夹逼定理1.1.1.2函数夹逼定理 1.1.2 两个重要极限1.1.2.1 极限公式11.1.2.1.1 证明1.1.2.1.2 数列的单调有界收敛准则1.1.2.1.2.1 二项式定理1.1.2.1.2.2 证明 1.1.2.2 极限公式21.1.2.2.1 证明(与1.2.1.2
高等数学的函数连续,可导,可微和偏导数连续的关系(多元)
结论(一元函数范畴内) 可导与连续的关系:可导必连续,连续不一定可导; 可微与连续的关系:可微与可导是一样的; 可积与连续的关系:可积不一定连续,连续必定可积; 可导与可积的关系:可导一般可积,可积推不出一定可导; 这个就不多说了。。。 下面是多元函数的关系 先上图 很显然函数连续,可导,可微和偏导数连续的关系可以从图中看出 函数连续不一定的函数可微(例子:y=|x|
考研 | 高等数学 Chapter4 不定积分
考研 | 高等数学 Chapter4 不定积分 文章目录 考研 | 高等数学 Chapter4 不定积分I. 定义II. 不定积分工具a. 基本公式b. 积分法case1: 第一类换元积分法case2: 第二类换元积分法1. **无理变有理**2. **三角代换, 平方和平方差**3. **分部积分法** III. 特殊函数的不定积分a. 有理函数case1: 假分式case2: 真分
【高等数学】不常见的三角函数与反三角函数
余切函数( y = cot x y=\cot x y=cotx) 基本关系: cot x = 1 tan x = cos x sin x \cot x=\dfrac{1}{\tan x}=\dfrac{\cos x}{\sin x} cotx=tanx1=sinxcosx图像: 反余切函数( y = a r c c o t x \newcommand{\arccot}{\
专升本高等数学考试知识点汇总(三)
河南专升本高等数学考点汇总(三) 第八章 多元函数的微分及应用重点考点一、多元函数微分法及应用1.多远函数的求导法2.全微分公式3.全微分的近似计算4.一阶全微分形式不变性5.隐函数求导公式 二、微分法在几何上的应用三、方形导数和梯度四、多元函数的极值及其求法1.二元函数极值判定2.求函数z=f(x,y)在Ψ(x,y)=0的条件下可能去极值点的步骤: 第九章 二重积分重点考点一、二重积分的
[渝粤题库]西北工业大学高等数学(上)
高等数学(上) 当时,与比较是( 非等价的同阶无穷小量 ). 当时,与等价的无穷小量是( ). 10、当x→0时,下面无穷小量中与x等价的无穷小量为( sin x ). 8.当时,函数与是等价无穷小量,则( 2 ). 8.当时,与2比较是( 非等阶的同阶无穷小量 ). 21.函数在内( 单调减少 ). 22.函数在( ).内单调减少. 函数的拐点是( ). 26.函数在( ).取极小值.
[渝粤教育] 中国地质大学 高等数学(二) 复习题
《高等数学》模拟题 一.单选题 1.设五次方程有五个不同的实根则方程最多有()个实根. A.5 B.4 C.3 D.2 2.函数在点处连续是在该点处可导的() A.必要但不充分条件 B.充分但不必要条件 C.充要条件 D.无关条件 3.设函数则在点处(). A.连续但不可导 B.连续且 C.连续且 D.不连续 4.设则=(). A.3 B.-3 C.6 D.-6 5.已知函数则在处 A