本文主要是介绍概率论考点之估计量（高等数学求最值），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
如题：2019年10月
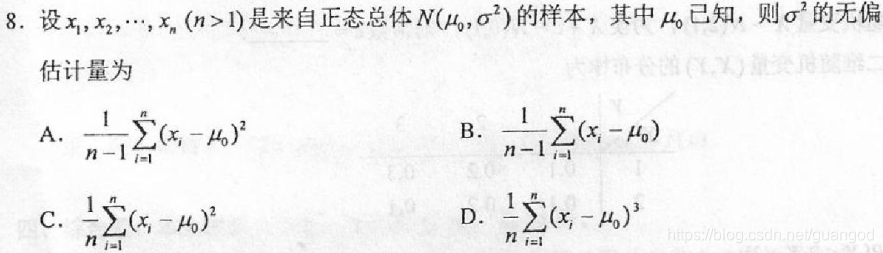
分析：新东西…………。大体看了下，应该是属于统计量及其分布的内容。
答案：根据《概率论复习之关于点估计》问题3中无偏性，样本k阶原点矩是总体k阶原点矩的无偏估计，原点矩的表达式为C
1、什么是统计量呢？？？？
用样本来表达的一个量，并且没有未知参数。如下定义：至于什么是样本？，详见扩展1：
2、什么又是无偏差？？？？首先搞明白什么是偏差？？详见扩展2
无偏差还有无偏估计量，属于统计推断的内容，就是由样本推断总体。有两种类型，参数估计和假设检验。
详见《概率论复习之关于点估计》
扩展：
1、什么是样本？？？
样本：总体里随机抽出的个体。
样本的关键要求:1、相互独立 2、跟总体同分布
样本的联合分布函数：
由于是样本间相互独立，所以各自的分布函数间也是独立的，并且都是和总体分布F(x)相同。这其实是上面关键要求的结果。还有一点为什么是相乘的关系？？？因为前提，不错，就是“前提”，要求联合分布，也就是说要完成联合分布就要全部取完所有样本，相当于一个事件分了n步去完成，所以是相乘的关系。
样本的联合概率密度：
样本的联合分布律：
2、什么是偏差呢？？？？基于样本均值的
样本均值:样本的算术平均值：
样本中的数据与样本均值的差，就是偏差。样本的所有偏差之和等于0。
样本均值重要定理：
样本均值的数学期望等于整体的数学期望。
样本均值的方差等于整体方差的n分之一倍。
注：
n为样本容量。
若总体分布服从
正态分布的话，则：
。
3、什么是样本方差？？？
定理：样本方差的数学期望等于西格马平方。
4、什么是卡方分布？？？独立的标准正态分布的平方和。称为自由度为n个卡方分布，n为参与自由度求和的个数，数学期望是n,方差是自由度的2倍。
什么是F分布？？？有两个自由度，分子来自卡方分布，分母也来自卡方分布，分子分母除以各自的自由度，大前提是独立。
F分布的性质：
什么是t分布？？？t分布的数学期望是0
需要背过的：
5、高等数学求最值，用导数求？
- 求函数的导数F'(X)
- 求出令F'(X)=0的x的值（称之为“驻点”）
- 判断驻点左右两侧F'(X)的正负，以此判断函数曲线的走向（F'(X)>0为上升，F'(X)<0为下降），左边上升、右边下降的驻点处的函数值为极大值，反之为极小值。
- 如果函数驻点较多，分段讨论，并可以列表、画图表达
- 求最大值，将所有极大值和函数定义域区间端点的函数值一起比较，取最大的，最小值亦然。
这篇关于概率论考点之估计量（高等数学求最值）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
