本文主要是介绍考研数学二复习笔记-高等数学-第二章 一元函数微分学,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.导数和微分
求导
使用导数的定义
f ′ ( x ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 或者 f ′ ( x ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x)=\lim_{x \to{x0}}\frac{f(x)-f(x0)}{x-x0} 或者f'(x)=\lim_{Δx \to0}\frac{f(x0+Δx)-f(x0)}{Δx} f′(x)=limx→x0x−x0f(x)−f(x0)或者f′(x)=limΔx→0Δxf(x0+Δx)−f(x0)
结论:
(1) lim x → x 0 f ( x ) + B x − x 0 = A 且 f ( x ) 在 x 0 处连续 , 可以推导出 lim x → x 0 f ( x ) = − B 和 f ′ ( x 0 ) = A \lim_{x \to{x0}}\frac{f(x)+B}{x-x0}=A且f(x)在x0处连续,可以推导出\lim_{x \to{x0}}f(x)=-B和f'(x0)=A limx→x0x−x0f(x)+B=A且f(x)在x0处连续,可以推导出limx→x0f(x)=−B和f′(x0)=A
( 2 ) f ( x ) = ∣ x − x 0 ∣ g ( x ) 且 g ( x ) 在 x 0 处连续 , f ′ ( x ) 在 x 0 处可到 ⇋ g ( x 0 ) = 0 (2)f(x)=|x-x0|g(x)且g(x)在x0处连续,f'(x)在x0处可到⇋g(x0)=0 (2)f(x)=∣x−x0∣g(x)且g(x)在x0处连续,f′(x)在x0处可到⇋g(x0)=0
注意点:
f(x)在x=a的某个邻域有定义,求f(x)在x=a处可导的充要条件是什么?
(1) lim x → + ∞ x [ f ( a + 1 x ) − f ( a ) ] 存在 \lim_{x \to+\infty}x[f(a+\frac{1}{x})-f(a)]存在 limx→+∞x[f(a+x1)−f(a)]存在 不能推出:只能说明存在右导数
(2) lim n → ∞ x [ f ( a + 1 n ) − f ( a ) ] 存在 \lim_{n \to\infty}x[f(a+\frac{1}{n})-f(a)]存在 limn→∞x[f(a+n1)−f(a)]存在 不能推出:n代表的是数列极限,也就是说n是正数,还是只能说明有右导数
(3) lim x → 0 f ( a + x ) − f ( a − x ) 2 x 存在 \lim_{x \to0}\frac{f(a+x)-f(a-x)}{2x}存在 limx→02xf(a+x)−f(a−x)存在 不能推出:虽然可以凑成两个导数定义的形式,但是可能a点是个分段点,也就不连续,更不可能有导数。
微分
现阶段可认为dx=Δx。dy=f'(x)dx
1.微分定义:Δy=AΔx+o(Δx),其中A与Δx无关
dy=AΔx
Δy-dy是Δx的高阶无穷小
(1)f’(x)>0且f’'(x)>0情况。此时Δy-dy>0
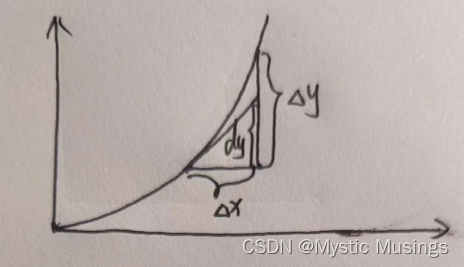
(2)f’(x)>0且f’'(x)<0情况。此时Δy-dy<0
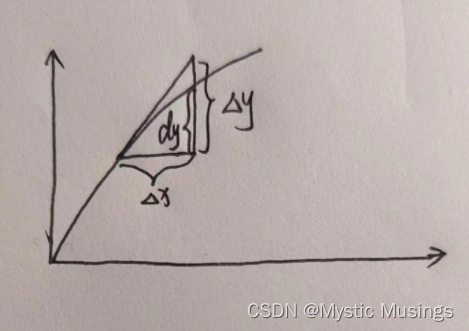
可导⇋可微
2.导数和微分计算
导数公式
(1) ( C ) ′ = 0 (C)'=0 (C)′=0
(2) ( x a ) ′ = a x a − 1 (x^a)'=ax^{a-1} (xa)′=axa−1
(3) ( a x ) ′ = a x l n a (a^x)'=a^xlna (ax)′=axlna
(4) ( e x ) ′ = e X (e^x)'=e^X (ex)′=eX
(5)(logax) ′ = 1 x l n a '=\frac{1}{xlna} ′=xlna1
(6) ( l n ∣ x ∣ ) ′ = 1 x (ln|x|)'=\frac{1}{x} (ln∣x∣)′=x1
(7) ( s i n x ) ′ = c o s x (sinx)'=cosx (sinx)′=cosx
(8) ( c o s x ) ′ = − s i n x (cosx)'=-sinx (cosx)′=−sinx
(9) ( t a n x ) ′ = s e c 2 x (tanx)'=sec^2x (tanx)′=sec2x
(10) ( c o t x ) ′ = − c s c 2 x (cotx)'=-csc^2x (cotx)′=−csc2x
(11) ( s e c x ) ′ = s e c x t a n x (secx)'=secx tanx (secx)′=secxtanx
(12) ( c s c x ) ′ = − c s c x c o t x (cscx)'=-cscx cotx (cscx)′=−cscxcotx
(13) ( a r c s i n ) ′ = 1 1 − x (arcsin)'=\frac{1}{\sqrt{1-x}} (arcsin)′=1−x1
(14) ( a r c c o x ) ′ = − 1 1 − x (arccox)'=-\frac{1}{\sqrt{1-x}} (arccox)′=−1−x1
(15) ( a r c t a n x ) ′ = 1 1 + x 2 (arctanx)'=\frac{1}{1+x^2} (arctanx)′=1+x21
(16) ( a r c c o t ) ′ = − 1 1 + x 2 (arccot)'=-\frac{1}{1+x^2} (arccot)′=−1+x21
长多项式求导
例如:
f(x)=(x-1)(x-2)…(x-50),则f’(1)=?
可以观察到x=1时x-1=0;可以将(x-2)(x-3)…(x-50)=g(x)
令f(x)=(x-1)g(x)
f’(x)=[(x-1)‘]g(x)+(x-1)g’(x)
带入1后只剩下g(x)部分了。
g(x)=(-1)(-2)…(-49)=-49!
反函数求导
d x d y = 1 d y d x \frac{dx}{dy}=\frac{1}{\frac{dy}{dx}} dydx=dxdy1
反函数二阶导: d 2 x d y 2 = d ( d x d y ) d y = d ( 1 f ′ ( x ) ) d y = d ( 1 f ′ ( x ) ) / d x d y / d x = f ′ ′ ( x ) − [ f ′ ( x ) ] 3 \frac{d^2x}{dy^2}=\frac{d(\frac{dx}{dy})}{dy}=\frac{d(\frac{1}{f'(x)})}{dy}=\frac{d(\frac{1}{f'(x)})/dx}{dy/dx}=\frac{f''(x)}{-[f'(x)]^3} dy2d2x=dyd(dydx)=dyd(f′(x)1)=dy/dxd(f′(x)1)/dx=−[f′(x)]3f′′(x)
隐函数求导
1.直接法(求具体函数某个点使用更容易)
直接对x和y求导,将y看作x的函数
2.公式法
将x和y全部移到等式的一边,分别求x和y的导,将y看作x的函数
F(x,y)=0;
F’x+ d y d x \frac{dy}{dx} dxdyF’y=0;
d y d x = − F ′ x F ′ y \frac{dy}{dx}=-\frac{F'x}{F'y} dxdy=−F′yF′x
3.全微分
求导技巧
y = f ( x ) g ( x ) y=f(x)^{g(x)} y=f(x)g(x)
1.对数法求导
lny = g(x)ln f(x)
求导: 1 y y ′ = g ′ ( x ) l n f ( x ) + g ( x ) 1 f ( x ) f ′ ( x ) \frac{1}{y}y'=g'(x)lnf(x)+g(x)\frac{1}{f(x)}f'(x) y1y′=g′(x)lnf(x)+g(x)f(x)1f′(x)
2.幂指转换
y = e g ( x ) l n f ( x ) y=e^{g(x)lnf(x)} y=eg(x)lnf(x)
再用复合函数求导法则
参数方程求导
x=x(t)
y=y(t)
d y d x = d y / d t d x / d t \frac{dy}{dx}=\frac{dy/dt}{dx/dt} dxdy=dx/dtdy/dt
二阶导
d 2 y d x 2 = d ( d y d x ) d x = y ′ ( t ) x ′ ( t ) d x = y ′ ( t ) x ′ ( t ) / d t d x / d t = y ′ ′ ( t ) x ′ ( t ) − y ′ ( t ) x ′ ′ ( t ) [ x ′ ( t ) ] 3 \frac{d^2y}{dx^2}=\frac{d(\frac{dy}{dx})}{dx}=\frac{\frac{y'(t)}{x'(t)}}{dx}=\frac{\frac{y'(t)}{x'(t)}/dt}{dx/dt}=\frac{y''(t)x'(t)-y'(t)x''(t)}{[x'(t)]^3} dx2d2y=dxd(dxdy)=dxx′(t)y′(t)=dx/dtx′(t)y′(t)/dt=[x′(t)]3y′′(t)x′(t)−y′(t)x′′(t)
结论
(1)奇函数导数为偶函数
(2)偶函数导数为奇函数
(3)周期函数的导数还是相同周期的周期函数
高阶求导数
1.泰勒展开式(麦克劳林)
在x=0处的展开式
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) x 2 2 ! + f ′ ′ ( 0 ) x 3 3 ! + . . . f ′ ′ ( 0 ) x n n ! f(x)=f(0)+f'(0)x+\frac{f''(0)x^2}{2!}+\frac{f''(0)x^3}{3!}+...\frac{f''(0)x^n}{n!} f(x)=f(0)+f′(0)x+2!f′′(0)x2+3!f′′(0)x3+...n!f′′(0)xn
f ( x ) = a 0 + a 1 ∗ x + a 2 ∗ x + . . . a n ∗ x f(x)=a0+a1*x+a2*x+...an*x f(x)=a0+a1∗x+a2∗x+...an∗x
求n阶导就是 f ( n ) = a n ∗ n ! f^{(n)}=an*n! f(n)=an∗n!
2.莱布尼茨公式
[ u ( x ) v ( x ) ] ( n ) = ∑ i = 0 n C ( i n ) u ( n − i ) ( x ) ∗ v ( i ) ( x ) [u(x)v(x)]^{(n)}=\sum_{i=0}^{n}C\binom{i}{n}u^{(n-i)}(x)*v^{(i)}(x) [u(x)v(x)](n)=∑i=0nC(ni)u(n−i)(x)∗v(i)(x)
3.中值定理,不等式与零点问题
中值定理:
1.费马引理:
f(x)在x0的邻域有定义,且f’(x0)是极值,f’(x0)=0;
证明:(以极大值为例)
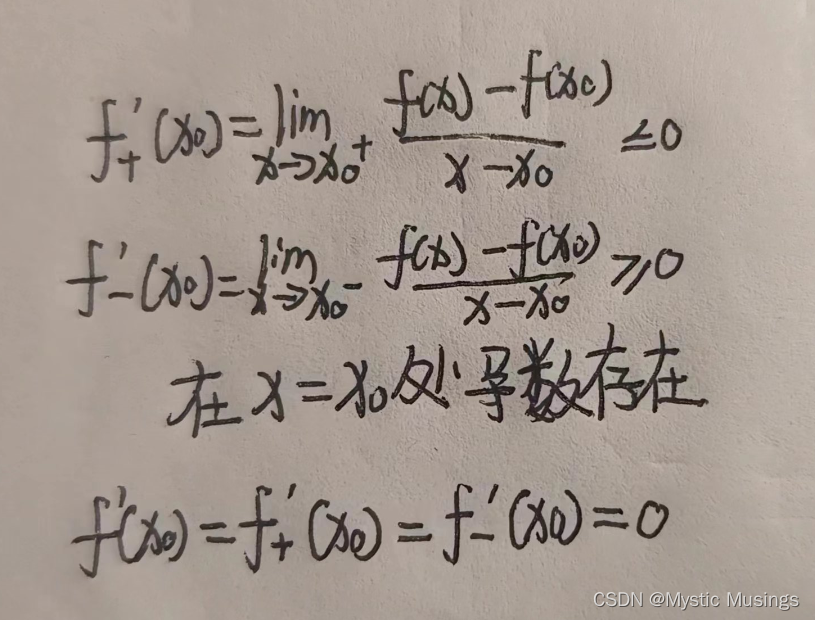
2.罗尔定理:
f(x)在[a,b]上连续,在(a,b)上可导,且f(a)=f(b)。至少存在一点ξ∈(a,b),使得f’(ξ)=0。
证明:

证明存在一个点 { ( 1 ) 无导数 : 辅助函数无积分 ( 2 ) 有导数 : 涉及积分考虑罗尔定理 { ( 1 ) 直接分析 ( 可以直接看出原函数 ) ( 2 ) 使用微分方程求解原函数 证明存在一个点\begin{cases} (1)无导数:辅助函数无积分 \\ (2)有导数:涉及积分考虑罗尔定理 \begin{cases}(1)直接分析(可以直接看出原函数)\\ (2)使用微分方程求解原函数 \end{cases} \end{cases} 证明存在一个点⎩ ⎨ ⎧(1)无导数:辅助函数无积分(2)有导数:涉及积分考虑罗尔定理{(1)直接分析(可以直接看出原函数)(2)使用微分方程求解原函数
{ ①将 ξ 改成 x ②将 y ′ 移到一边 , 复合函数放一边 ③解微分方程得到 c = g ( x , y ) ④ y = f ( x ) 令 F ( x ) = f ( x , f ( x ) ) \begin{cases}①将ξ改成x \\ ②将y'移到一边,复合函数放一边 \\ ③解微分方程得到c=g(x,y) \\ ④y=f(x) 令F(x)=f(x,f(x)) \end{cases} ⎩ ⎨ ⎧①将ξ改成x②将y′移到一边,复合函数放一边③解微分方程得到c=g(x,y)④y=f(x)令F(x)=f(x,f(x))
例题以及证明

设方程参考

推广结论: f ( n ) ( x ) 有 k 个零点 , 说明 f ( x ) 最多 n + k 个零点。 f^{(n)}(x)有k个零点,说明f(x)最多n+k个零点。 f(n)(x)有k个零点,说明f(x)最多n+k个零点。
3.拉格朗日中值定理:
f(x)在[a,b]连续,在(a,b)可导,至少存在一点ξ∈(a,b)使得 f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) f(b)-f(a)=f'(ξ)(b-a) f(b)−f(a)=f′(ξ)(b−a) ξ∈(a,b)
证明:
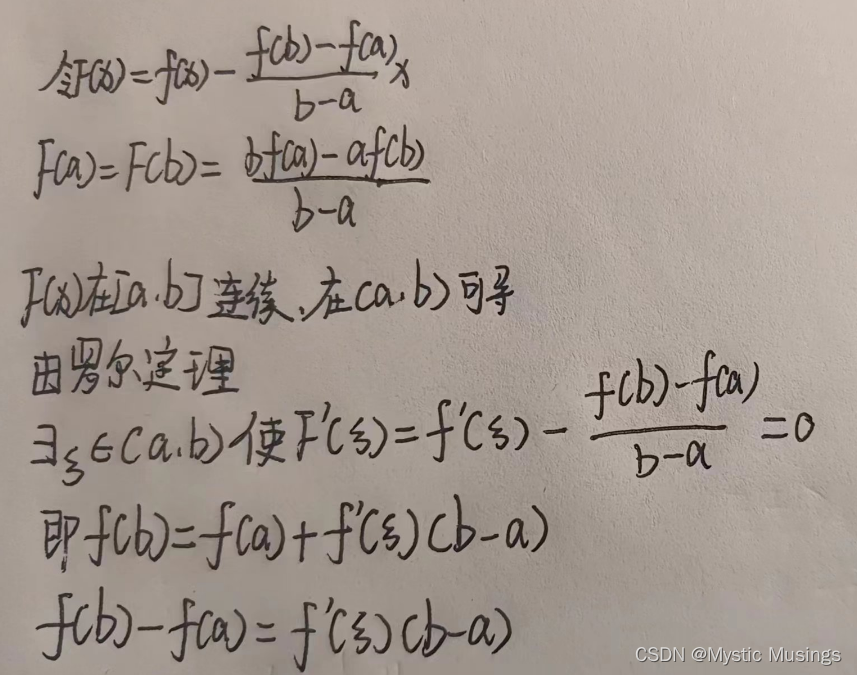
4.柯西中值定理:
f(x)和g(x)在闭区间[a,b]连续,在(a,b)可导,g’(0)不为0,至少存在一点ξ∈(a,b)使得
f ( b ) − f ( a ) g ( b ) − g ( a ) = f ′ ( ξ ) g ′ ( ξ ) \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(ξ)}{g'(ξ)} g(b)−g(a)f(b)−f(a)=g′(ξ)f′(ξ)
证明:

当证明题中出现两个函数,需要考虑柯西中值定理!!!
不等式证明:
基本不等式:
s i n < x < t a n x sin<x<tanx sin<x<tanx x ∈ ( 0 , π 2 ) x∈(0,\frac{π}{2}) x∈(0,2π)
e x ≥ x + 1 e^x≥x+1 ex≥x+1 x ∈ r , 等于在 x = 0 处成立 x∈r,等于在x=0处成立 x∈r,等于在x=0处成立
x ≥ l n ( x + 1 ) ≥ 1 1 + x x≥ln(x+1)≥\frac{1}{1+x} x≥ln(x+1)≥1+x1 x≥-1成立,x=0取等号
a r c t a n x < x < a r c s i n x arctanx<x<arcsinx arctanx<x<arcsinx 0<x<1
零点定理:
不涉及积分的题目用零点定理,
涉及积分就用罗尔定理
4.导数应用
极值:
- 极值应该满足一阶导为0,二阶导不为0
- 驻点是二阶导为0的点
极值第一充分条件:邻域左右导数异号
极值第二充分条件:一阶导为0,二阶导不为0
拐点:
拐点第一必要条件:若x=x0处为拐点,则f’'(x0)=0
拐点第一充分条件:邻域二阶导左右异号
拐点第二充分条件:二阶导为0.三阶导不为0
拐点第三充分条件: f ′ ( x 0 ) = f ′ ′ ( x 0 ) = . . . = f ( n − 1 ) ( x 0 ) = 0 , f ( n ) ( x 0 ) ! = 0 , 且 n 为大于二的偶数 f'(x0)=f''(x0)=...=f^{(n-1)}(x0)=0,f^{(n)}(x0)!=0,且n为大于二的偶数 f′(x0)=f′′(x0)=...=f(n−1)(x0)=0,f(n)(x0)!=0,且n为大于二的偶数
{ ( 1 ) f ( n ) ( x 0 ) > 0 时 f ( x 0 ) 为极小值 ( 2 ) f ( n ) ( x 0 ) < 0 时 f ( x 0 ) 为极大值 \begin{cases}(1)f^{(n)}(x0)>0时f(x0)为极小值\\ (2)f^{(n)}(x0)<0时f(x0)为极大值 \end{cases} {(1)f(n)(x0)>0时f(x0)为极小值(2)f(n)(x0)<0时f(x0)为极大值
渐近线:
斜渐近线和水平渐近线不能共存!!! !!!
水平渐近线:
如果x趋于无穷处极限是一个常数A,存在y=A这个水平渐近线。
垂直渐近线:
如果间断点x0处的左极限或右极限为无穷,存在垂直x=x0渐近线
斜渐近线:
x趋于无穷处 f ( x ) x = a 且 f ( x ) − a x = b ,则 y = a x + b 是斜渐近线 \frac{f(x)}{x}=a且f(x)-ax=b,则y=ax+b是斜渐近线 xf(x)=a且f(x)−ax=b,则y=ax+b是斜渐近线(正负无穷都要判断)
弧微分和曲率:
y=f(x),在f(x)有连续导数。存在弧微分 d s = 1 + y ′ d x ds=\sqrt[]{1+y'}dx ds=1+y′dx
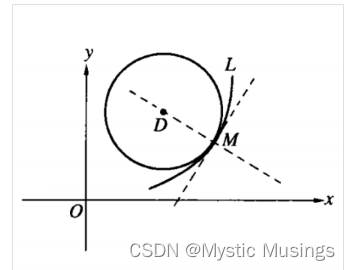
y=f(x)有二阶导,有曲率 k = ∣ y ′ ′ ∣ ( 1 + y ′ 2 ) 3 2 , ρ = 1 k k=\frac{|y''|}{(1+y'2)^{\frac{3}{2}}},ρ=\frac{1}{k} k=(1+y′2)23∣y′′∣,ρ=k1,结论:【1.曲线和圆有公共切线.2.曲线和圆有相同的y,y’,y’’ 3.L和C相同切线和曲率】
这篇关于考研数学二复习笔记-高等数学-第二章 一元函数微分学的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








