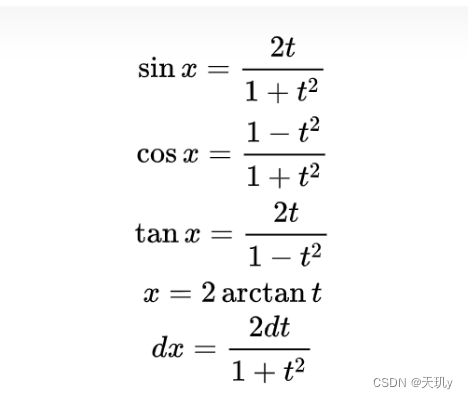一元函数专题
考研数学二复习笔记-高等数学-第二章 一元函数微分学
1.导数和微分 求导 使用导数的定义 f ′ ( x ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 或者 f ′ ( x ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x)=\lim_{x \to{x0}}\frac{f(x)-f(x0)}{x-x0} 或者f'(x)=\lim_{
一元函数积分学——刷题(16
目录 1.题目:2.解题思路和步骤:3.总结:小结: 1.题目: 比较这两种题的求解方法 2.解题思路和步骤: 3.13: 这个题就很适合用万能公式,因为可以把1+t2消掉: 也可以用三角恒等式: 3.14: 虽然万能公式总是可以求出三角函数的积分,但是不一定是最好的方法,比如这类题可以使用其他方法: 3.总结: 万能公式: 小结: 关注我给大
2020张宇1000题【好题收集】【第二章:一元函数微分学】
文章目录 二.一元函数微分学2.42.192.22 导数计算2.26【证明题】2.40【乘积的求导阔以转换成对数】2.442.48【坑大林】【利用零点求n阶导】2.49【求 a r c t a n x arctanx arctanx的n阶导数】???(1)(2) 2.53【极坐标求切线方程】2.65【考极值的定义】 中值定理、方程的根、不等式2.95【用定义说明极值】2.96【辅助函数证明题
2020张宇1000题【好题收集】【第三章:一元函数积分学】
文章目录 三.一元函数积分学性质概念3.2(结论)【导函数与原函数的周期性】 3.43.7 一元积分比大小3.103.13 定积分定义计算3.173.22 换元法一元函数积分复杂与特色计算3.873.883.893.903.923.933.943.95 反常积分判敛与计算3.1033.1043.1053.1253.1303.133(积分曲线)3.136(绕直线旋转) 一元积分的物理应用3.1
《微积分:一元函数积分学》——不定积分与定积分的存在定理
1、原函数(不定积分)存在定理 (1)连续函数 f(x) 必有原函数 F(x) (2)含有第一类间断点、无穷间断点的函数 f(x) 在包含该间断点的区间内必没有原函数 F(x) 2、定积分存在定理 (1)f (x) 在 [a,b] 上连续,则 存在 (2)若 f (x) 在 [a,b] 上有界,且只有有限个间断点则 存在 另一个充要条件:若 f (x)在 [a,b] 上
《微积分:一元函数微分学》——狄利克雷函数
定义 性质 狄利克雷函数是一个有界的偶函数,且任何有理数都是它的周期,它没有最小的周期 应用 函数 f(x) 在点 x=x0 可导,那么 f(x) 在点 x=x0 处必然连续,如果函数 f(x) 在点 x=x0 处可导,并不一定存在点 x=x0 的某个邻域,使得函数在这个邻域内连续 使用狄利克雷函数构造一个反例 根据 ”无穷小量乘有界函数仍然是无穷小量“ 可知上述结果
《微积分:一元函数微分学》——经典不等式
不等式1 设 a,b 为实数,则有 不等式(2)的推广 离散情况:设 a1、a2、a3、...、an为实数,则 连续情况:设 f(x) 在 [a,b] 上可积,则 不等式2 设 a1、a2、a3、...、an > 0,则 (当且仅当 a1=a2=...=an 时等号成立) (当且仅当 a1=a2=...=an 时等号成立) 通常我们用
《微积分:一元函数微分学》——判断拐点的三个充要条件
二阶可导点是拐点的必要条件 设 存在,且点 (x0,f(x0) ) 为曲线拐点,则 判断拐点的第一充分条件 设 f(x) 在 x=x0 处连续,在点 x=x0 的某去心邻域 内二阶导数存在,且在该点的左右邻域内 变号 则点 (x0,f(x0) ) 为曲线拐点 判断拐点的第二充分条件 设 f(x) 在 x=x0 的某邻域内三阶可导,且 ,则点 (x0,f(x0) )
《微积分:一元函数微分学》——判断极值的三个充要条件
一阶可导点是极值点的必要条件 设 f(x) 在 x=x0 处可导,且在点 x0 处取得极值,则必有 判断极值的第一充分条件 设 f(x) 在 x=x0 处连续,且在 x0 的某去心邻域 内可导 x0 极小值点x0 极大值点 判断极值的第二充分条件 设 f(x) 在 x=x0 处二阶可导,且 x0 极大值点 x0 极小值点 判断极值的第三充分条件 设
《微积分:一元函数微分学》——罗尔定理
罗尔定理 设 f(x) 满足 [a,b]上连续(a,b)内可导f(a)=f(b) 则 使得 推广: 1、f(a)=f(b)变为 a的左极限=b的右极限 2、f(a)=f(b)=正无穷、f(a)=f(b)=负无穷 3、(a,b)可为无穷区间,此时使用端点的极限值即可
【C++】STL 算法 ④ ( 函数对象与谓词 | 一元函数对象 | “ 谓词 “ 概念 | 一元谓词 | find_if 查找算法 | 一元谓词示例 )
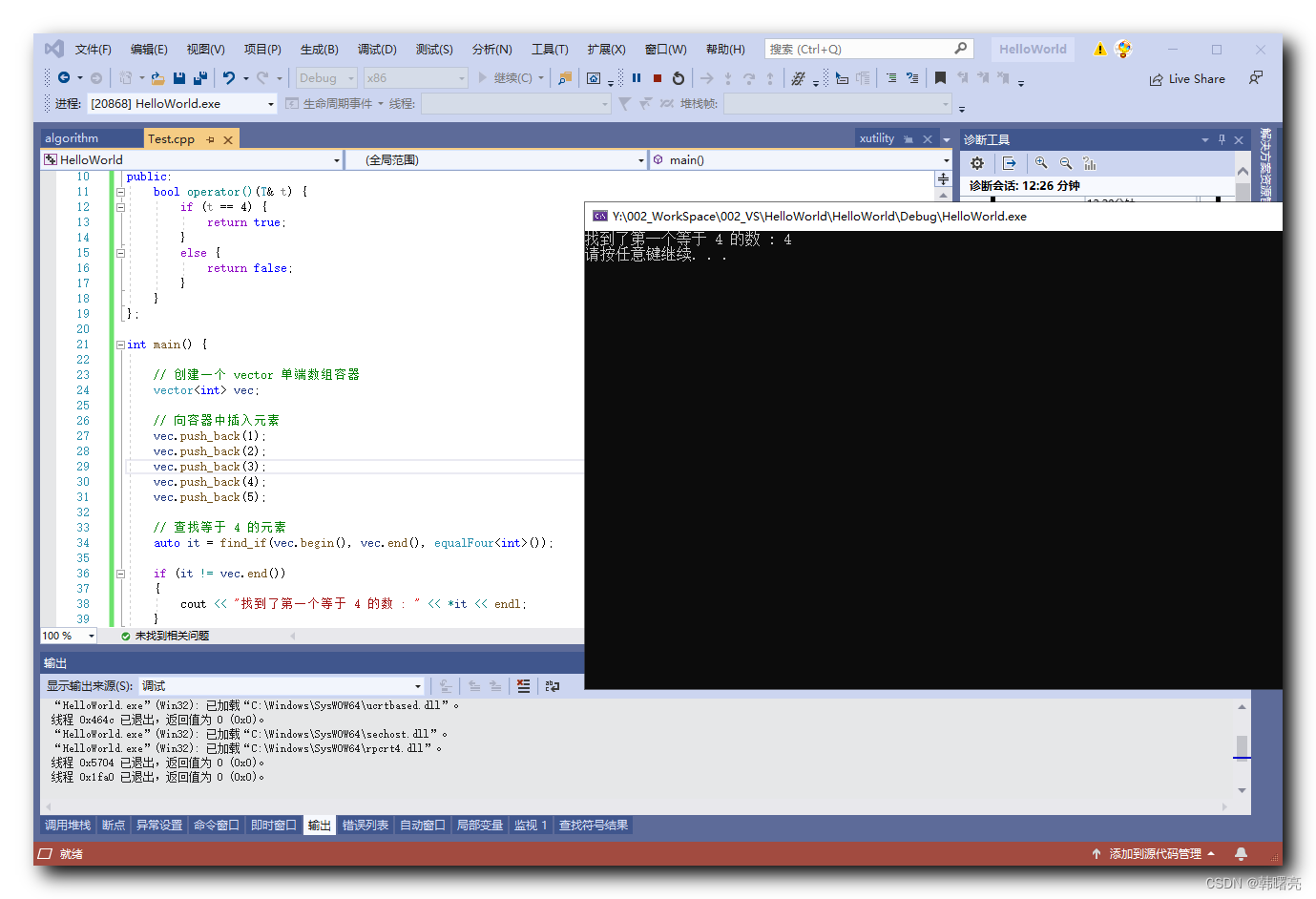
文章目录 一、函数对象与谓词1、一元函数对象2、" 谓词 " 概念3、find_if 查找算法 二、一元谓词示例1、代码示例 - 一元谓词示例2、执行结果 一、函数对象与谓词 1、一元函数对象 " 函数对象 " 是通过 重载 函数调用操作符 () 实现的 operator() , 函数对象 可以 像普通函数一样被调用 , 但同时它们 还可以拥有状
一元函数微分学——刷题(12
目录 1.题目:2.解题思路和步骤:3.总结:小结: 1.题目: 2.解题思路和步骤: 注意两个y的区别即可 都可以在图中画出来,所以就非常好比较 3.总结: 理解两种y的区别即可 小结: 关注我给大家分享更多有趣的知识,以下是个人公众号,提供 ||代码兼职|| ||代码问题求解|| 由于本号流量还不足以发表推广,搜我的公众号即可:
一元函数微分学——刷题(2
目录 1.题目:2.解题思路和步骤:3.总结:小结: 1.题目: 2.解题思路和步骤: 这个题目可能看上去比较吓人,但是,又很简单;因为一切都太明确了,跟着我仔细看一下: 首先,左边那个等式说明(这个肯定能懂,因为这就是导数定义): 其次,由于分母除以一个趋近于零的分子等于常数A,说明f(a)趋近于b 问题相当于求的是: 于是我们化简,把上面已知的内容代入即可求得最
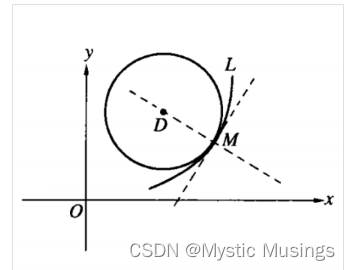
《数学竞赛辅导》-一元函数微分学-7.23
这个专栏用于博主备战16年9月的全国大学生数学竞赛(非数学)的习题集,因此在记录过程中以题目为主,几乎不会呈现理论定理的推导过程。 这篇文章用于记录一元微分学相关的题目。所谓一元微分学就是一个变量的函数,进行多次求导,相应的一元积分学就是一元函数多次积分,改变变量的个数就是多元函数微分学、多元函数积分学,这个在陈启浩的《大学生数学竞赛指导(非数学)》中的目录中给出,对于梳理知识体系会有一
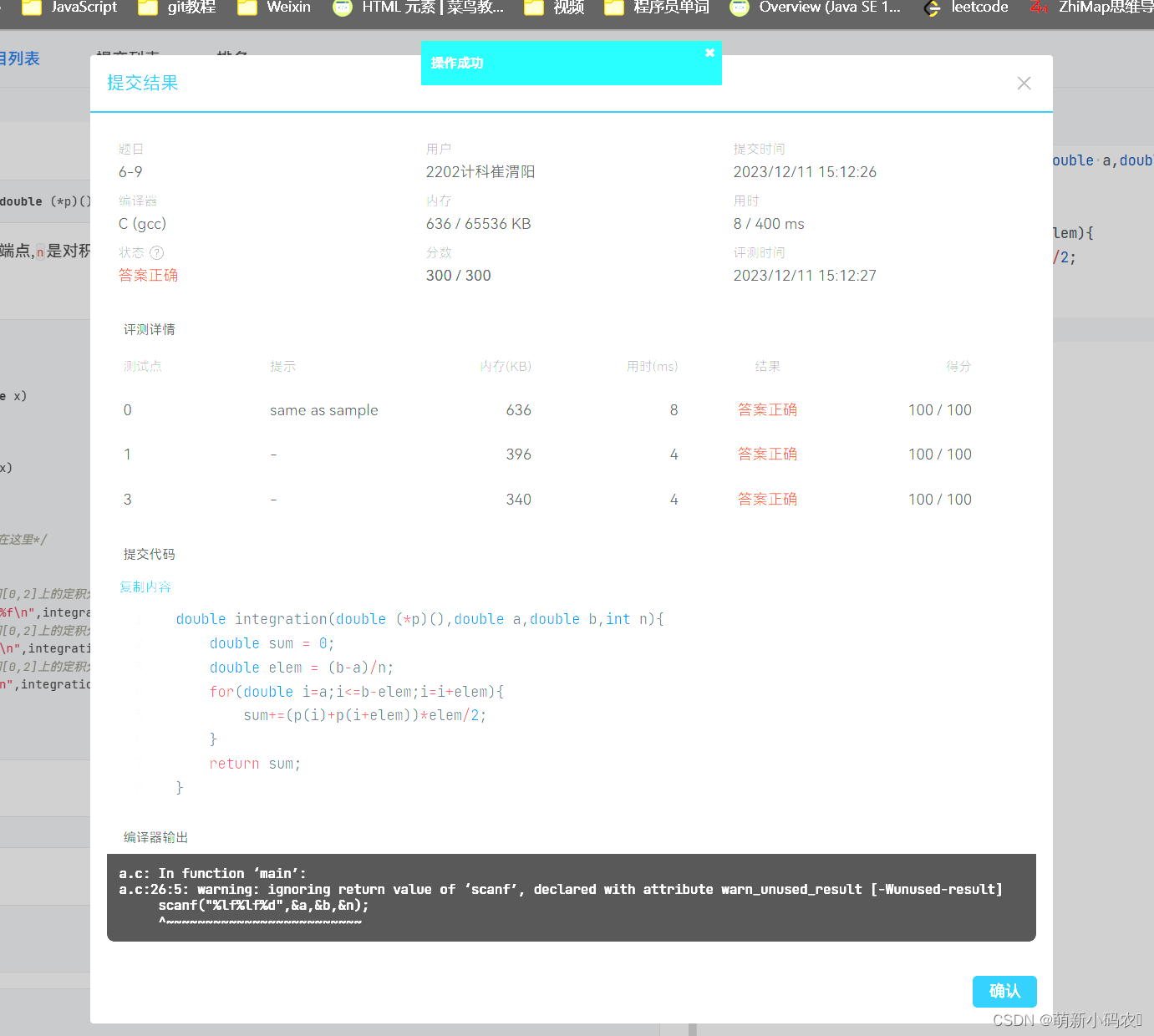
6-9 求一元函数定积分
一元函数f(x)在区间[a,b]上定积分∫abf(x)dx的几何意义是被积函数与横坐标轴以及直线x=a和直线x=b围成的曲边形的面积。依据几何意义求定积分的方法是将这个区域按x轴方向等分成若干个细小的条状区域,每个小区域近似于一个梯形(如图所示),计算出所有小梯形面积之和就可计算出区域面积的近似值。区间划分的越细求得的结果越精确。 现在要求用梯形法编写一个求一元定积分的
数学基础30讲: 第四讲 一元函数微分学的概念与计算
目录 概述1、概念1.1 导数的概念导数定义的引入导数定义的广义化导数定义的两种表达形式单侧导数导数存在的充要条件导数不存在的情况导数的集合意义与高阶导数概念例题 1.2 微分的概念 2、计算2.1 四则运算2.2 分段函数的导数2.3 复合函数的导数与微分不变性2.4 反函数的导数2.5 参数方程求导2.6 隐函数求导2.7 对数求导2.8 幂指函数求导2.9 高阶导数2.10 变限积分求
《微积分:一元函数积分学》——不定积分与定积分的存在定理
1、原函数(不定积分)存在定理 (1)连续函数 f(x) 必有原函数 F(x) (2)含有第一类间断点、无穷间断点的函数 f(x) 在包含该间断点的区间内必没有原函数 F(x) 2、定积分存在定理 (1)f (x) 在 [a,b] 上连续,则 存在 (2)若 f (x) 在 [a,b] 上有界,且只有有限个间断点则 存在 另一个充要条件:若 f (x)在 [a,b] 上
高等数学强化2:一元函数微分学
1.导数、微分概念 几何意义: 导数:在点 x 0 x_{0} x0的切线斜率。 微分:切线上的增量。 f ( x ) f(x) f(x)n阶可导,用洛必达最多用到n-1阶,即 f n − 1 ( x ) f^{n-1}(x) fn−1(x)。 f ( x ) f(x) f(x)n阶连续可导,用洛必达最多用到n阶,即 f n ( x ) f^{n}(x) fn(x)。 2
一元函数积分学的应用
目录:点我 思维导图下载:点我 一、研究对象 函数 f ( x ) . f(x). f(x).函数列 f n ( x ) . f_n(x). fn(x).用参数方程所给出的函数;偏导函数 ∂ f ∂ x . \frac{\partial f}{\partial x}. ∂x∂f.变限积分函数 ∫ a x f ( t ) d t . \int_{a}^{x}f(t)dt. ∫a
高数 | 【一元函数积分学】定积分、变限积分 一元函数积分学李林880 巧解例题
一、定积分的概念、性质及几何意义 巧解:利用奇偶性,快速选出答案。 利用图形帮助解题。 设出具体函数。 二、定积分的计算 1.利用几何意义 2.换元法巧解 3.区间平移 本题也可用用区间再现 4.绝对值
高等数学——一元函数微分学
系列文章目录 高等数学——函数、极限和连续高等数学——一元函数微分学高等数学——一元函数积分学高等数学——微分方程高等数学——多元函数微分学高等数学——二重积分 文章目录 系列文章目录版权声明名词解释常用数学符号常用希腊字符读音初等数学相关知识幂、根式和对数常用的三角函数值三角函数变换一元二次方程求解充分条件和必要条件切线方程、斜率和法线隐函数极坐标参数方程 导数微分微分中值定理求导
高数:第三章:一元函数积分学
文章目录 一、不定积分(一)两个基本概念:原函数、不定积分(二)原函数的存在性:原函数存在定理(三)不定积分的性质(四)基本积分公式(五)三种主要积分法1.凑微分 (第一类换元法)2.换元法 (第二类换元法)①三角代换②根式代换③倒代换 3.分部积分法4.其他技巧:积分公式、分项积分法(拆两项)、 -1 +1 、上下同乘 (六)三类常见可积函数积分1.有理函数积分: ∫ R ( x ) d