高等数学强化2：一元函数微分学

1.导数、微分概念

几何意义：
导数：在点$x_0$的切线斜率。
微分：切线上的增量。

$f(x)$n阶可导，用洛必达最多用到n-1阶，即$f^{n-1}(x)$。

$f(x)$n阶连续可导，用洛必达最多用到n阶，即$f^n(x)$。

2.求导法则

反函数导数

高阶导数4个常用公式：

3.导数与微分概念题

${\lim }_{x\to x_0}\frac{f(\phi (x))}{\psi (x)}$可导要求：
1.φ (x)->0且φ (x) $\ne$ 0
2.φ (x)可正可负。
3.φ (x)与ψ(x)同阶。

函数，绝对值函数可导间的关系：

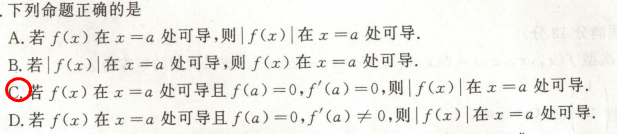
上述结论应用：

函数可导性与绝对值可导关系：

导数的几何意义：

分段复合函数的问题：
内外函数不可导 推不出 整个函数一定不可导。

复合函数求导：

4.隐函数的导数

参数方程代公式求解二阶导：

$${\frac{d^{2}y}{d{x}^2}}_{t=0}=\frac{y^{\prime \prime }(0)x^{\prime }(0)-x^{\prime \prime }(0)y^{\prime }(0)}{x^{\prime 3}(0)}$$

5.反函数导数：

设$y=f(x)$的反函数为$x=\phi (y)$，则
一阶导数：
$${\phi }^{\prime }(y)=\frac{1}{f^{\prime }(x)}$$
二阶导数：
$${\phi }^{\prime \prime }(y)=-\frac{f^{\prime \prime }(x)}{f^{\prime 3}(x)}$$

6.对数求导法

7.高阶导数

找规律：

降幂：

泰勒公式求解导数：
$a_n=\frac{f^{(n)}(0)}{n!}$

考研真题回顾，判断不可导点