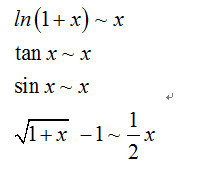微分学专题
考研高数(对比一元微分学和一元积分学概念)
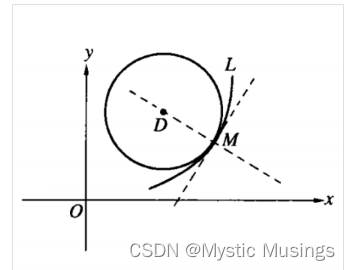
1.一元微分学的概念和一元积分学的概念 一元微分 1.导数 函数一点可导的充要条件:左右导数均存在且相等(也可说左右极限存在且相等) 函数一点可导的必要条件:若f(x)在一点可导,则f(x)在该点连续。反之未必。 2.导数的几何意义 函数y=f(x) 在x=x0处的导数 f′(x0),表示曲线y=f(x)在点P(x0,f(x0))处的切线的斜率k。 注意:一点的导数存在-->
第三章:00023工本高数第二章多元函数的微分学考点
1.考点一:一元极限基础知识 不考一元极限,但作为基础知识必不可少 1.了解运用两个重要极限 1. lim x → 0 s i n x x
【数学基础篇】---详解极限与微分学与Jensen 不等式
一、前述 数学基础知识对机器学习还有深度学习的知识点理解尤为重要,本节主要讲解极限等相关知识。 二、极限 1.例子 当x趋于0的时候,sin(x)与tan(x)都趋于0。但是哪一个趋于0的速度更快一些呢? 我们考察这两个函数的商的极限, 所以当 x → 0 的时候,sin(x) 与 tan(x) 是同样级别的无穷小。 2.相关定理 如果三个函数满足 f(x) ≤ g(x) ≤ h(x),
考研数学二复习笔记-高等数学-第二章 一元函数微分学
1.导数和微分 求导 使用导数的定义 f ′ ( x ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 或者 f ′ ( x ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x)=\lim_{x \to{x0}}\frac{f(x)-f(x0)}{x-x0} 或者f'(x)=\lim_{
微分学<4>——微分中值定理
索引 微分中值定理极值定义4.1 极大(小)值定理4.1 Fermat引理定理4.2 Rolle定理 Lagrange中值定理定理4.3 Lagrange中值定理定理4.4 Cauchy中值定理 导数对函数性质的刻画Jensen不等式 微分中值定理 极值 定义4.1 极大(小)值 若存在 x 0 x_{0} x0的邻域 U ( x 0 , δ ) U\left ( x_{
2020张宇1000题【好题收集】【第二章:一元函数微分学】
文章目录 二.一元函数微分学2.42.192.22 导数计算2.26【证明题】2.40【乘积的求导阔以转换成对数】2.442.48【坑大林】【利用零点求n阶导】2.49【求 a r c t a n x arctanx arctanx的n阶导数】???(1)(2) 2.53【极坐标求切线方程】2.65【考极值的定义】 中值定理、方程的根、不等式2.95【用定义说明极值】2.96【辅助函数证明题
《微积分:一元函数微分学》——狄利克雷函数
定义 性质 狄利克雷函数是一个有界的偶函数,且任何有理数都是它的周期,它没有最小的周期 应用 函数 f(x) 在点 x=x0 可导,那么 f(x) 在点 x=x0 处必然连续,如果函数 f(x) 在点 x=x0 处可导,并不一定存在点 x=x0 的某个邻域,使得函数在这个邻域内连续 使用狄利克雷函数构造一个反例 根据 ”无穷小量乘有界函数仍然是无穷小量“ 可知上述结果
《微积分:一元函数微分学》——经典不等式
不等式1 设 a,b 为实数,则有 不等式(2)的推广 离散情况:设 a1、a2、a3、...、an为实数,则 连续情况:设 f(x) 在 [a,b] 上可积,则 不等式2 设 a1、a2、a3、...、an > 0,则 (当且仅当 a1=a2=...=an 时等号成立) (当且仅当 a1=a2=...=an 时等号成立) 通常我们用
《微积分:一元函数微分学》——判断拐点的三个充要条件
二阶可导点是拐点的必要条件 设 存在,且点 (x0,f(x0) ) 为曲线拐点,则 判断拐点的第一充分条件 设 f(x) 在 x=x0 处连续,在点 x=x0 的某去心邻域 内二阶导数存在,且在该点的左右邻域内 变号 则点 (x0,f(x0) ) 为曲线拐点 判断拐点的第二充分条件 设 f(x) 在 x=x0 的某邻域内三阶可导,且 ,则点 (x0,f(x0) )
《微积分:一元函数微分学》——判断极值的三个充要条件
一阶可导点是极值点的必要条件 设 f(x) 在 x=x0 处可导,且在点 x0 处取得极值,则必有 判断极值的第一充分条件 设 f(x) 在 x=x0 处连续,且在 x0 的某去心邻域 内可导 x0 极小值点x0 极大值点 判断极值的第二充分条件 设 f(x) 在 x=x0 处二阶可导,且 x0 极大值点 x0 极小值点 判断极值的第三充分条件 设
《微积分:一元函数微分学》——罗尔定理
罗尔定理 设 f(x) 满足 [a,b]上连续(a,b)内可导f(a)=f(b) 则 使得 推广: 1、f(a)=f(b)变为 a的左极限=b的右极限 2、f(a)=f(b)=正无穷、f(a)=f(b)=负无穷 3、(a,b)可为无穷区间,此时使用端点的极限值即可
一元函数微分学——刷题(12
目录 1.题目:2.解题思路和步骤:3.总结:小结: 1.题目: 2.解题思路和步骤: 注意两个y的区别即可 都可以在图中画出来,所以就非常好比较 3.总结: 理解两种y的区别即可 小结: 关注我给大家分享更多有趣的知识,以下是个人公众号,提供 ||代码兼职|| ||代码问题求解|| 由于本号流量还不足以发表推广,搜我的公众号即可:
一元函数微分学——刷题(2
目录 1.题目:2.解题思路和步骤:3.总结:小结: 1.题目: 2.解题思路和步骤: 这个题目可能看上去比较吓人,但是,又很简单;因为一切都太明确了,跟着我仔细看一下: 首先,左边那个等式说明(这个肯定能懂,因为这就是导数定义): 其次,由于分母除以一个趋近于零的分子等于常数A,说明f(a)趋近于b 问题相当于求的是: 于是我们化简,把上面已知的内容代入即可求得最
《数学竞赛辅导》-一元函数微分学-7.23
这个专栏用于博主备战16年9月的全国大学生数学竞赛(非数学)的习题集,因此在记录过程中以题目为主,几乎不会呈现理论定理的推导过程。 这篇文章用于记录一元微分学相关的题目。所谓一元微分学就是一个变量的函数,进行多次求导,相应的一元积分学就是一元函数多次积分,改变变量的个数就是多元函数微分学、多元函数积分学,这个在陈启浩的《大学生数学竞赛指导(非数学)》中的目录中给出,对于梳理知识体系会有一
数学基础30讲: 第四讲 一元函数微分学的概念与计算
目录 概述1、概念1.1 导数的概念导数定义的引入导数定义的广义化导数定义的两种表达形式单侧导数导数存在的充要条件导数不存在的情况导数的集合意义与高阶导数概念例题 1.2 微分的概念 2、计算2.1 四则运算2.2 分段函数的导数2.3 复合函数的导数与微分不变性2.4 反函数的导数2.5 参数方程求导2.6 隐函数求导2.7 对数求导2.8 幂指函数求导2.9 高阶导数2.10 变限积分求
高等数学强化2:一元函数微分学
1.导数、微分概念 几何意义: 导数:在点 x 0 x_{0} x0的切线斜率。 微分:切线上的增量。 f ( x ) f(x) f(x)n阶可导,用洛必达最多用到n-1阶,即 f n − 1 ( x ) f^{n-1}(x) fn−1(x)。 f ( x ) f(x) f(x)n阶连续可导,用洛必达最多用到n阶,即 f n ( x ) f^{n}(x) fn(x)。 2
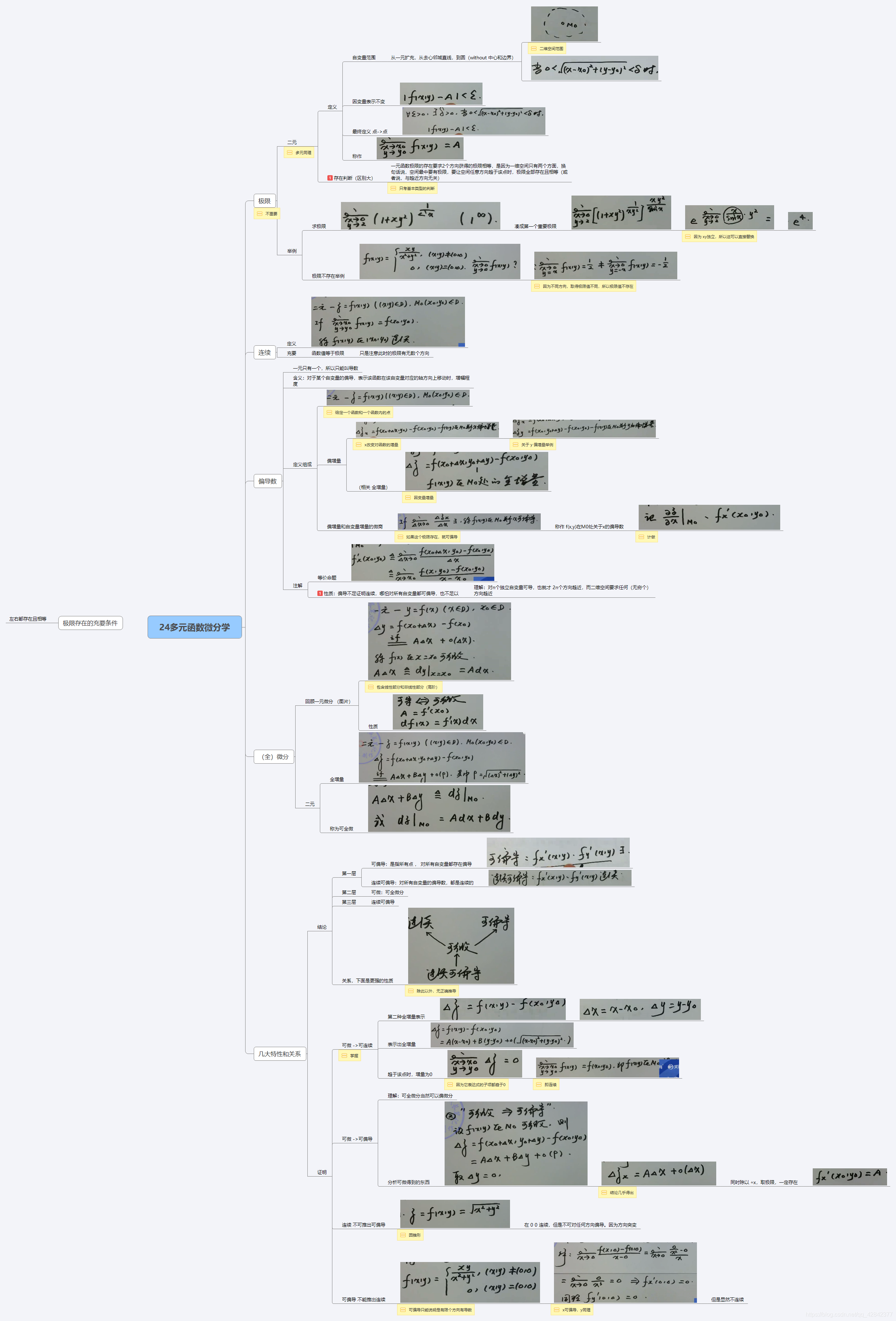
高等数学强化5:多元函数微分学(1) 重极限、连续、偏导数、微分
1.考点 2.常考题型 多元求重极限 判断重极限是否存在 3.偏导数 二元偏导数其实是带入某一增量后的一元导数,解题方法:先代后求。 几何意义:曲面 z ( x , y ) z(x,y) z(x,y)在 x = x 0 x=x_{0} x=x0或 y = y 0 y=y_{0} y=y0处的交线的斜率 4.全微分 5.一元、多元函数连续、可导、可微的
【数学基础篇】---详解极限与微分学与Jensen 不等式
一、前述 数学基础知识对机器学习还有深度学习的知识点理解尤为重要,本节主要讲解极限等相关知识。 二、极限 1.例子 当x趋于0的时候,sin(x)与tan(x)都趋于0。但是哪一个趋于0的速度更快一些呢? 我们考察这两个函数的商的极限, 所以当 x → 0 的时候,sin(x) 与 tan(x) 是同样级别的无穷小。 2.相关定理 如果三个函数满足 f(x) ≤ g(x) ≤ h(x),
高等数学——一元函数微分学
系列文章目录 高等数学——函数、极限和连续高等数学——一元函数微分学高等数学——一元函数积分学高等数学——微分方程高等数学——多元函数微分学高等数学——二重积分 文章目录 系列文章目录版权声明名词解释常用数学符号常用希腊字符读音初等数学相关知识幂、根式和对数常用的三角函数值三角函数变换一元二次方程求解充分条件和必要条件切线方程、斜率和法线隐函数极坐标参数方程 导数微分微分中值定理求导