本文主要是介绍【数学基础篇】---详解极限与微分学与Jensen 不等式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、前述
数学基础知识对机器学习还有深度学习的知识点理解尤为重要,本节主要讲解极限等相关知识。
二、极限
1.例子
当x趋于0的时候,sin(x)与tan(x)都趋于0。但是哪一个趋于0的速度更快一些呢?
我们考察这两个函数的商的极限,
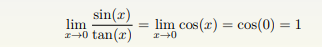
所以当 x → 0 的时候,sin(x) 与 tan(x) 是同样级别的无穷小。
2.相关定理
如果三个函数满足 f(x) ≤ g(x) ≤ h(x), 而且他们都在 x0 处有极限,那么
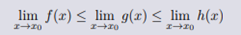
重要极限:

三、微分学
微分学的核心思想:逼近。
1.函数导数:
如果一个函数 f(x) 在 x0 附近有定义,而且存在极限。
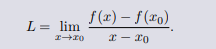
那么 f(x) 在 x0 处可导且导数 f ′ (x0) = L。
无穷小量表述:线性逼近。
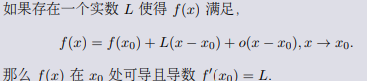
Definition(函数的高阶导数)
如果函数的导数函数仍然可导,那么导数函数的导数是二阶导数,二阶导数函数的导数是三阶导数。
一般地记为
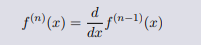
或者进一步
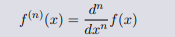
导数是对函数进行线性逼近,高阶导数是对导数函数的进一步逼近,因为没有更好的办法,所以数学家选择继续使用线性逼近。
Example (初等函数的导数)
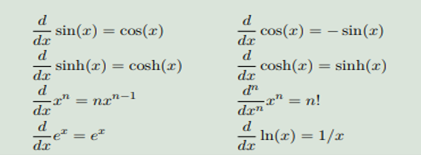
2.微分学:多元函数

且 Lx,Ly 分别是 f 在 x, y 方向上的偏导数。一般记为
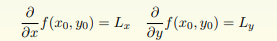
3.Definition (高阶偏导数)

并且二阶偏导数为
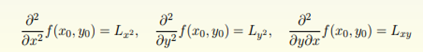
4.Example (偏导数的例子)
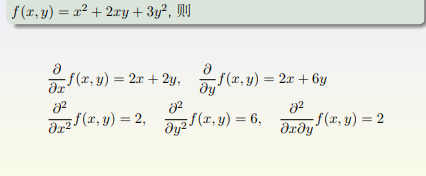
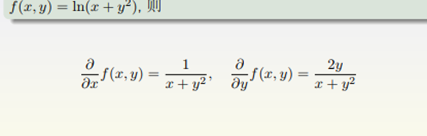

5.求导法则
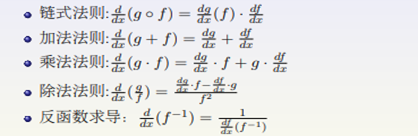
6.总结
微分学的核心思想是逼近。
一阶导数:线性逼近
二阶导数:二次逼近
导数计算:求导法则
四、泰勒级数
1.泰勒/迈克劳林级数: 多项式逼近。

2.泰勒级数: 例子
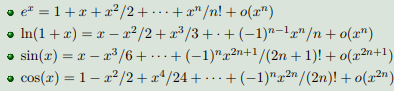
3.应用
泰勒级数是一元微分逼近的顶峰,所以有关于一元微分逼近的问题请尽情使用。
罗比塔法则
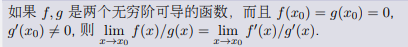
证明:
因为是在 x0 附近的极限问题,我们使用泰勒级数来思考这个问题
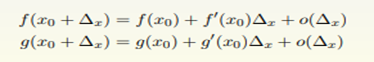
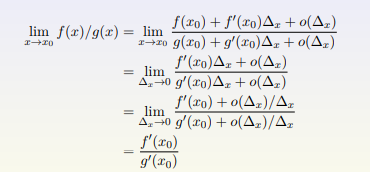
4.小结 (泰勒级数)
泰勒级数本质是多项式逼近
特殊函数的泰勒级数可以适当记一下
泰勒级数可以应用于很多与逼近相关的问题。
五、牛顿法与梯度下降法
很多机器学习或者统计的算法最后都转化成一个优化的问题。也就是求某一个损失函数的极小值的问题,在本课范围内我们考虑可微分的函数极小值问题。
1.优化问题
对于一个无穷可微的函数f(x),如何寻找他的极小值点。
极值点条件。
全局极小值:如果对于任何 x˜, 都有 f(x∗) ≤ f(˜x),那么 x∗ 就是全局极小值点。
局部极小值:如果存在一个正数 δ 使得,对于任何满足 |x˜ − x∗| < δ 的 x˜, 都有 f(x∗) ≤ f(˜x),那么 x∗ 就是局部极 小值点。(方圆 δ 内的极小值点)
不论是全局极小值还是局部极小值一定满足一阶导数/梯度 为零,f ′ = 0 或者 ∇f = 0。
2.局部极值算法
这两种方法都只能寻找局部极值这两种方法都要求必须给出一个初始点 x0
数学原理:牛顿法使用二阶逼近(等价于使用二阶泰勒级数),梯度下降法使用一阶逼近
牛顿法对局部凸的函数找到极小值,对局部凹的函数找到极大值,对局部不凸不凹的可能会找到鞍点。
梯度下降法一般不会找到最大值,但是同样可能会找到鞍点。
当初始值选取合理的情况下,牛顿法比梯度下降法收敛速度快。
牛顿法要求估计二阶导数,计算难度更大.
3.牛顿法
首先在初始点x0处,写出二阶泰勒级数。
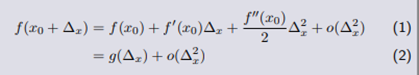
 多变量函数二阶逼近
多变量函数二阶逼近


4.梯度下降法:多变量函数一阶逼近
如果函数 f(x) 是个多元函数,x 是一个向量,在 x0 处对f做线性逼近。

5.小结 (牛顿法与梯度下降法)
牛顿法与梯度下降法本质上都是对目标函数进行局部逼近,因为是局部逼近所以也只能寻找局部极值。
牛顿法收敛步骤比较少,但是梯度下降法每一步计算更加简单,牛顿法不仅给出梯度的方向还给出具体应该走多少。梯度法的r只能自己定义。
不同的算法之间很难说哪一个更好,选择算法还要具体问题具体分析(这也是数据科学家存在的意义之一)。
梯度本身是向着最大方向的,加个负号才是向着最小方向的。
六、凸函数与琴生不等式
1.Definition (凸函数)
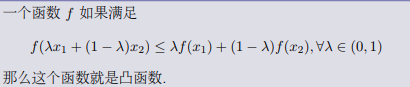
把如上定义中的 ≤ 换成<,那么这个函数就叫做严格凸函数。
2.(凸函数判断准则)

如果 f 是多元函数,x 是个向量,那么 f 是凸函数的条件变为Hf 是一个半正定矩阵。
3.凸函数重要性质: 琴生不等式
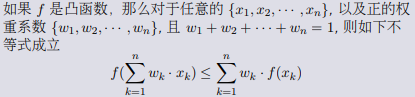
配合视频食用,风味更佳→《人工智能必备数学基础》
TESRA超算网络旗下T-CCP社区已上线,社区由高校AI社团及AI爱好者组成,社区包含学习视频、学习笔记、数据集模型、算法竞赛等内容,新用户注册还能免费领取算力训练,欢迎前来体验。立即边学边练>>>

这篇关于【数学基础篇】---详解极限与微分学与Jensen 不等式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




