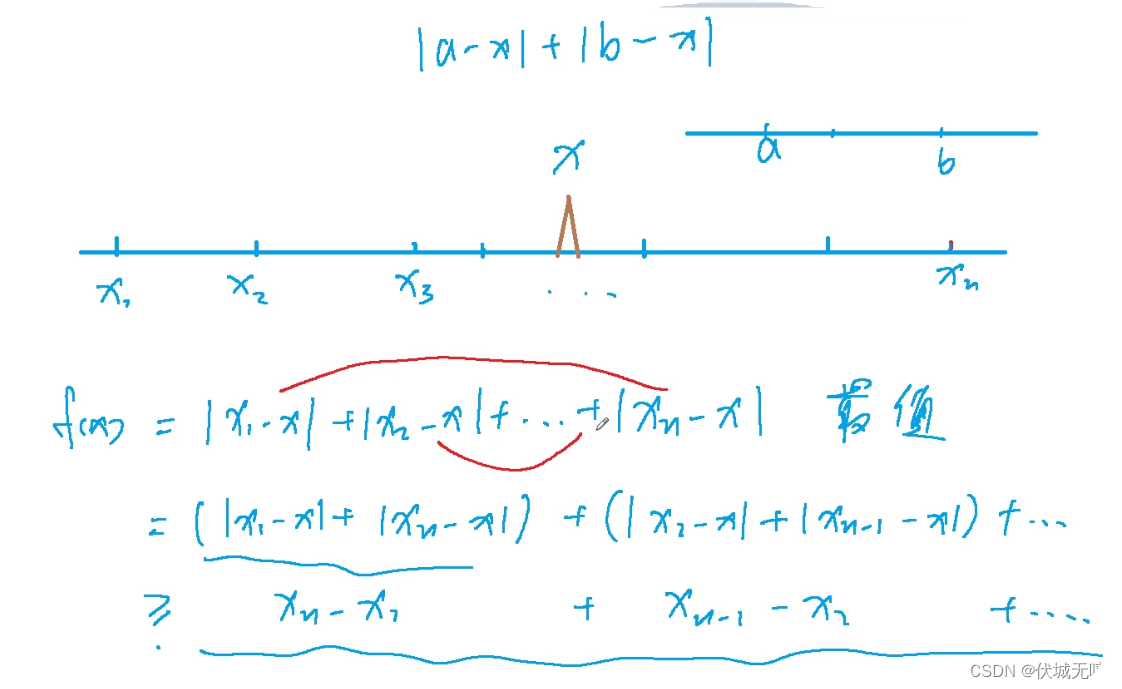不等式专题

【高中数学/基本不等式】若正数a,b满足a＞b,且1/(a+b)+1/(a-b)=1,则3a+2b的最小值是？

【问题】若正数a,b满足a>b,且1/(a+b)+1/(a-b)=1,则3a+2b的最小值是？【来源】《解题卡壳怎么办高中数学解题智慧点剖析》P38 余继光苏德矿合著浙江大学出版社出版【如何破题】 1/(a+b)+1/(a-b)=1这个关系式挺复杂，展开后更乱(用三角函数也帮不上忙)，而3a+2b这个表达式相对简单；如果想让两者相乘，可以用配方的手段，得出的结果一部分能

gurobi约束条件使用大全(`model.addConstr()`添加单个约束和`model.addConstrs()`添加多个约束和强不等式约束）

文章目录 gurobi约束条件`model.addConstr()`添加单个约束`model.addConstrs()`添加多个约束强不等式约束 gurobi约束条件 model.addConstr()添加单个约束约束可以是线性、不等式或等式。Gurobi支持添加单个约束和多重约束。例子： model.addConstr(x + y == 5, "eq_const

概率的三条基本公理 | 布尔不等式的应用（举例）

概率论的三条基本公理由俄罗斯数学家柯尔莫哥洛夫（Andrey Kolmogorov）在1933年提出，被称为柯尔莫哥洛夫公理。它们构成了现代概率论的基础。这三条公理如下：公理 1：非负性公理 2：规范性公理 3：可加性布尔不等式对于任意的事件集合 { A 1 , A 2 , … , A n } \{A_1, A_2, \ldots, A_n\} {A1,A2,…,An}

概率论与数理统计 -- 大数定理及切比雪夫不等式整理

大数定理、切比雪夫不等式及其推导大数定律弱大数定律（Weak Law of Large Numbers, WLLN）弱大数定律指出，当试验次数 (n) 趋向无穷大时，样本平均值 (\bar{X_n}) 与期望值 (\mu) 之间的差异以概率收敛于0。数学上表示为： ∀ ϵ > 0 , lim ⁡ n → ∞ P ( ∣ 1 n ∑ i = 1 n X i − μ ∣ ≥ ϵ ) =

算法数据结构（三十六）----四边形不等式技巧

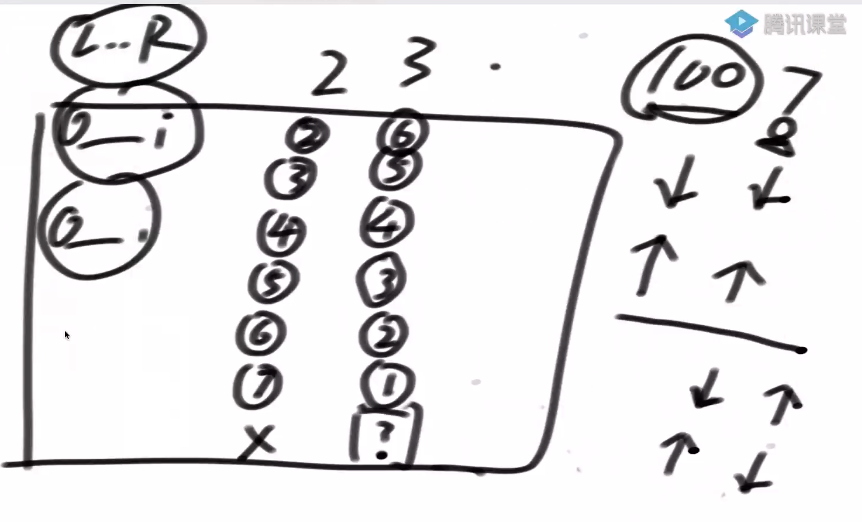
题目一给定一个非负数组arr，长度为N，那么有N-1种方案可以把arr切成左右两部分每一种方案都有，min{左部分累加和，右部分累加和} 求这么多方案中，min{左部分累加和，右部分累加和}的最大值是多少？整个过程要求时间复杂度O(N) //暴力求解public static int bestSplit1(int[] arr) {if (arr == null || arr.l

马尔可夫和比奈梅-切比雪夫不等式

目录一、说明二、自然界的极限性三、马尔可夫不等式 3.1 最早提出 3.2 马尔可夫不等式的证明四、 Bienaymé–Chebyshev 不等式 4.1 简要回顾Bienaymé–Chebyshev 不等式的历史 4.2 Bienaymé — Chebyshev 不等式的证明五、弱大数定律（及其证明） 5.1 定律陈述 5.2 弱大数定律的证明一、说明

Hoeffding不等式的证明

这个不等式是Azuma鞅不等式的一个特例见Azuma不等式，下面的证明不用复杂的理论。从wikipedia摘抄的。注意，markov不等式中的y是x，不等式右边的E(X) ,换成E(|X|)。证明过程假设X是非负随机变量下面几个typo，然后下面X在[a,b]区间的概率为1，应该是P(X \in [a,b]) = 1 Hoeffding不等式如下：设是取值在区间中的随机变量，令

hihoCoder挑战赛14 题目1 : 不等式

时间限制: 10000ms 单点时限: 1000ms 内存限制: 256MB 描述给定n个关于X的不等式，问最多有多少个成立。每个不等式为如下的形式之一： X < C X <= C X = C X > C X >= C 输入第一行一个整数n。以下n行，每行一个不等式。数据范围: 1<=N<=50,0<=C<=1000 输出一行一个整数，表示最多可以同时成

已知不等式：1！+2！+···+m!n,请计算并输出满足该不等式的m的整数解。

#include <stdio.h>#include <stdlib.h>int main(){int i,n;int sum=0,term=1;printf("Input n:");scanf("%d",&n);for(i=1;sum<n;i++){term*=i;sum+=term;if(sum>=n)break;}printf("m<=%d",i);r

51Nod 1022 石子归并 V2 (划分型dp四边形不等式优化)

石子归并以前做过好几次，是经典划分型dp题之一，一直用的O(n3)的正常dp方法，也从未想过该怎么去优化它。直到昨天做这道题，n的范围由往常的100改为了1000，老方法一直超时，苦不堪言，搜到有个四边形不等式的优化方法，看帖子，画式子，拉着学长帮忙推导，总算是大概弄明白了一点。 dp(i,j) = min(dp(i,k)+dp(k+1,j)) + w(i,j);(i < j

信息论中的不等式

1. 凸函数定义凸函数 f(x) f(x)定义有两个方法： 1） f′′(x)≥0 f^{''}(x) \ge 0 2） λf(x1)+(1−λf(x2)≥f(λx1+(1−λ)xx) \lambda f(x_1)+(1-\lambda f(x_2) \ge f(\lambda x_1+(1-\lambda)x_x) 用这两种定义来证明函数凸性各有利弊。常用的凸函数有： −logx,

【ZZULIOJ】1058: 求解不等式（Java）

目录题目描述输入输出样例输入 Copy 样例输出 Copy 提示 code 题目描述已知不等式 1！+2！+3！+...+m！‹n,请编程对用户指定的n值计算并输出满足该不等式的m的整数解。输入输入一个整数n，n为int范围内的正整型。输出输出m的取值范围，具体格式见输出样例。样例输入 Copy 2000000000 样例输出 Copy

SVM中的拉格朗日乘子法解决不等式约数问题（KKT）

https://blog.csdn.net/howardemily/article/details/79949646

最小质因数 == 最大质因数，不等式秒了！

起因：在洛谷做题遇到了这道题~ 一看咿呀，又是道数学题~ 首先我们要了解一下，什么是质数？我记得好像有年高考题的前几题好像考了这玩意来着，质数的概念好像在小学学过，上了初中后基本都没有用过了~ 质数就是素数，我们以前应该写过一个程序叫判断某个范围的数里面有多少个素数，其实在这里我们就已经了解过质数的概念了~ 以下是GPT回答的参考：质数和素数在数

【数学基础篇】---详解极限与微分学与Jensen 不等式

一、前述数学基础知识对机器学习还有深度学习的知识点理解尤为重要，本节主要讲解极限等相关知识。二、极限 1.例子当x趋于0的时候，sin(x)与tan(x)都趋于0。但是哪一个趋于0的速度更快一些呢？我们考察这两个函数的商的极限，所以当 x → 0 的时候，sin(x) 与 tan(x) 是同样级别的无穷小。 2.相关定理如果三个函数满足 f(x) ≤ g(x) ≤ h(x)，

Hive SQL必刷练习题：排列组合问题【通过join不等式】

排列组合问题【通过join不等式】这种问题，就是数学的排列不等式，一个队伍只能和其余队伍比一次，不能重复方法1：可以直接通过join，最后on是一个不等式【排列组合问题的解决方式】方法2：也可以是提前多加一列，加上一个序号方法1 selectt1.team_name team_name_2,t2.team_name team_name_1from(selectteam

HDU 5699 货物运输 (二分 + 不等式判断好题)

货物运输 Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) Total Submission(s): 17 Accepted Submission(s): 3 Problem Description 公元2222年，l国发生了一场战争。

海明不等式推导

根据教材：假设传输的数据为： 1001011 在2^n位上不放信息位，放校验位则 1 000 011 这样可能还有点难看出规律但是当校验位达到6位时表格中n代表的就是校验位此时校验位和其能校验的最大信息位为： 1->0 2->1 3->4 4->11 5->26 这样校验位和信息位的关系就能看出来了设校验位的位数为n，其能表示的最大信息

第六章贪心（二）（排序不等式、绝对值不等式、推公式）

（一）排序不等式 913 排队打水，每个人都有自己杯子的容量从小到大排序，总时间最小； #include<bits/stdc++.h>using namespace std;//148 合并果子const int N=1e5+10;int main(){priority_queue< int,vector<int>,greater<int> >heap;long long

matlab解不等式方程/解不等式方程组

用solve来解不等式方程 ,因为我们想得到的是一个范围，所以在solve中要加一个'ReturnConditions'，'true' -----------------------------------------------------------(●'◡'●)-------------------------------------------------------------

不等式的证明之一

不等式的证明证明下述不等式之一证明证明下述不等式之一设 a , b , c a,b,c a,b,c 是正实数，请证明下述不等式： 1 < a a 2 + b 2 + b b 2 + c 2 + c c 2 + a 2 ≤ 3 2 1<\frac{a}{\sqrt{a^2 + b^2}} + \frac{b}{\sqrt{b^2 + c^2}} + \frac{c}{\

高中数学：不等式

一、性质 1、同向可加性 2、同向同正可乘 3、正数乘方开方（n∈Z，n≥2）常见题型 1、比较大小分式比较大小，先去分母作差法比较大小带根号的无理数比较大小，直接两边开方因式分解（较难） 2、求范围换元法含绝对值的不等式（画图法，分类讨论法，两边平方法）含参数的绝对值二、基本不等式常见题型 1、和积式 2、非齐次式 3、齐次式 4、多次利用不等式解题思路（供参考

C++ 贪心绝对值不等式货仓选址

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN 。现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。输入格式第一行输入整数 N 。第二行 N 个整数 A1∼AN 。输出格式输出一个整数，表示距离之和的最小值。数据范围 1≤N≤100000 , 0≤Ai≤40000 输

C++ 贪心排序不等式排队打水

有 n 个人排队到 1 个水龙头处打水，第 i 个人装满水桶所需的时间是 ti ，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？输入格式第一行包含整数 n 。第二行包含 n 个整数，其中第 i 个整数表示第 i 个人装满水桶所花费的时间 ti 。输出格式输出一个整数，表示最小的等待时间之和。数据范围 1≤n≤105 , 1≤ti≤104 输入样例： 7 3 6 1

【NOIP2013模拟11.7A组】不等式(solve)

【NOIP2013模拟11.7A组】不等式(solve) 题目【NOIP2013模拟11.7A组】不等式(solve) (File IO): input:solve.in output:solve.out Time Limits: 1000 ms Memory Limits: 262144 KB Detailed Limits Description 小z热衷于数学。今天数学课的内容是

AI-数学-高中-25-三角函数一图像解决三角函数不等式

原作者视频：【三角函数】【考点精华】1图像解决三角函数不等式问题(基础）_哔哩哔哩_bilibili 1.三角函数图像法； 2.不好画图像时：任意角的三角函数图像，在象限中比较，在4个象限中寻找角度的关系。示例1：示例2-2：示例2-3：