本文主要是介绍【高等数学】不常见的三角函数与反三角函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
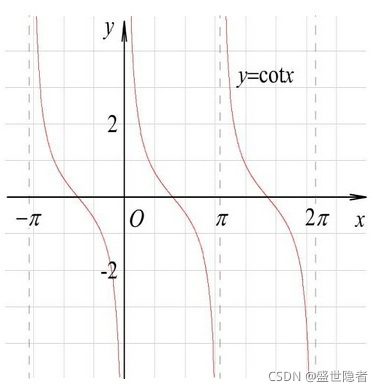
- 余切函数( y = cot x y=\cot x y=cotx)
- 基本关系: cot x = 1 tan x = cos x sin x \cot x=\dfrac{1}{\tan x}=\dfrac{\cos x}{\sin x} cotx=tanx1=sinxcosx
- 图像:
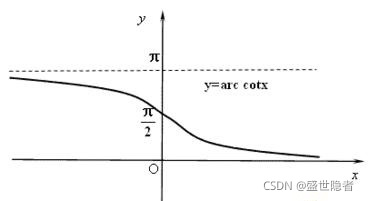
- 反余切函数( y = a r c c o t x \newcommand{\arccot}{\mathrm{arccot}\,}y=\arccot x y=arccotx)
- 定义域: ( − ∞ , ∞ ) (-\infin,\infin) (−∞,∞)
- 值域: ( 0 , π ) (0,\pi) (0,π)
- 反函数: y = cot x , x ∈ ( 0 , π ) y=\cot x,x\in (0,\pi) y=cotx,x∈(0,π)
- 图像:
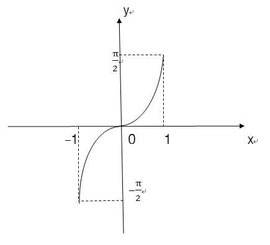
- 反正弦函数( y = arcsin x y=\arcsin x y=arcsinx)
- 定义域: [ − 1 , 1 ] [-1,1] [−1,1]
- 值域: [ − π 2 , π 2 ] [-\dfrac{\pi}{2},\dfrac{\pi}{2}] [−2π,2π]
- 反函数: y = sin x , x ∈ [ − π 2 , π 2 ] y=\sin x, x\in[-\dfrac{\pi}{2},\dfrac{\pi}{2}] y=sinx,x∈[−2π,2π]
- 图像:
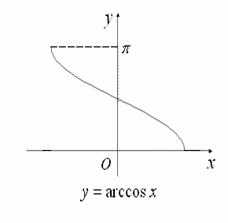
- 反余弦函数( y = arccos x y=\arccos x y=arccosx)
- 定义域: [ − 1 , 1 ] [-1,1] [−1,1]
- 值域: [ 0 , π ] [0,\pi] [0,π]
- 图像:
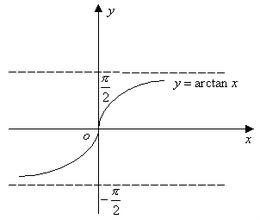
- 反正切函数( y = arctan x y=\arctan x y=arctanx)
- 定义域: ( − ∞ , ∞ ) (-\infin,\infin) (−∞,∞)
- 值域: ( − π 2 , π 2 ) (-\dfrac{\pi}{2},\dfrac{\pi}{2}) (−2π,2π)
- 反函数: y = tan x , x ∈ ( − π 2 , π 2 ) y=\tan x,x\in (-\dfrac{\pi}{2},\dfrac{\pi}{2}) y=tanx,x∈(−2π,2π)
- 图像:
这篇关于【高等数学】不常见的三角函数与反三角函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





