三角函数专题
数学基础 -- 微积分之三角函数幂的积分
三角函数幂的积分处理 1. 积分形式 1.1 ∫ sin m ( x ) cos n ( x ) d x \int \sin^m(x) \cos^n(x) \, dx ∫sinm(x)cosn(x)dx 1.1.1 当 n n n 为奇数时 分离奇数次幂 如果 cos n ( x ) \cos^n(x) cosn(x) 是奇数次幂,可以将其分解为 cos n −
【高数】三角函数积累
1.两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1
Canvas 动画: atan2 三角函数与鼠标跟随效果
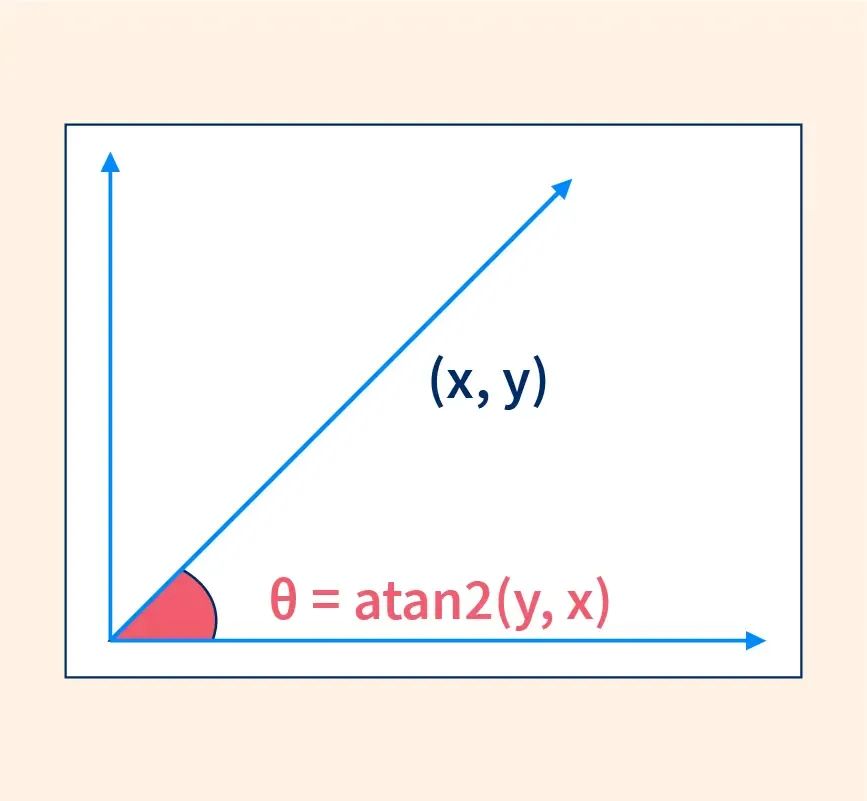
这个案例展示了如何使用HTML5的Canvas和JavaScript实现一个动态效果:在画布上绘制一个箭头,并让它实时跟随鼠标移动。这个小项目不仅有趣,还能帮助你理解编程和基本数学概念的实际应用。 项目需求 我们的目标是在一个画布上绘制一个箭头,并让这个箭头随着鼠标的移动自动旋转,始终指向鼠标的位置。 数学基础知识:atan2函数 在这个项目中,最关键的数学概念是atan2函数,它帮助我们计算
【题库】—— 买铅笔 三角形分类 小玉家的电费 三角函数
一、NOIP2016 普及组 买铅笔 #include<bits/stdc++.h>using namespace std;int main(){long long c,n,a,b,sum,min;//一定注意数据类型,如果改成int,亲测洛谷给分52cin>>n;for(int i=0;i<3;i++){ cin>>a>>b;c=ceil(1.0*n/a);//向上取整,也可以直接判断余
【MATLAB源码-第225期】基于matlab的计算器GUI设计仿真,能够实现基础运算,三角函数以及幂运算。
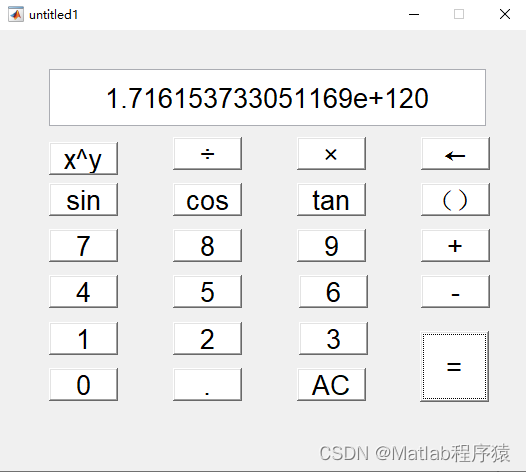
操作环境: MATLAB 2022a 1、算法描述 界面布局 计算器界面的主要元素分为几大部分:显示屏、功能按钮、数字按钮和操作符按钮。 显示屏 显示屏(Edit Text):位于界面顶部中央,用于显示用户输入的表达式和计算结果。当前显示内容为“81^63+88-995/44”,这表示用户可以输入复杂的数学表达式,包括指数运算、加减乘除等。 功能按钮 界面左侧一列是功能按钮,包
C++三角函数和反三角函数的使用
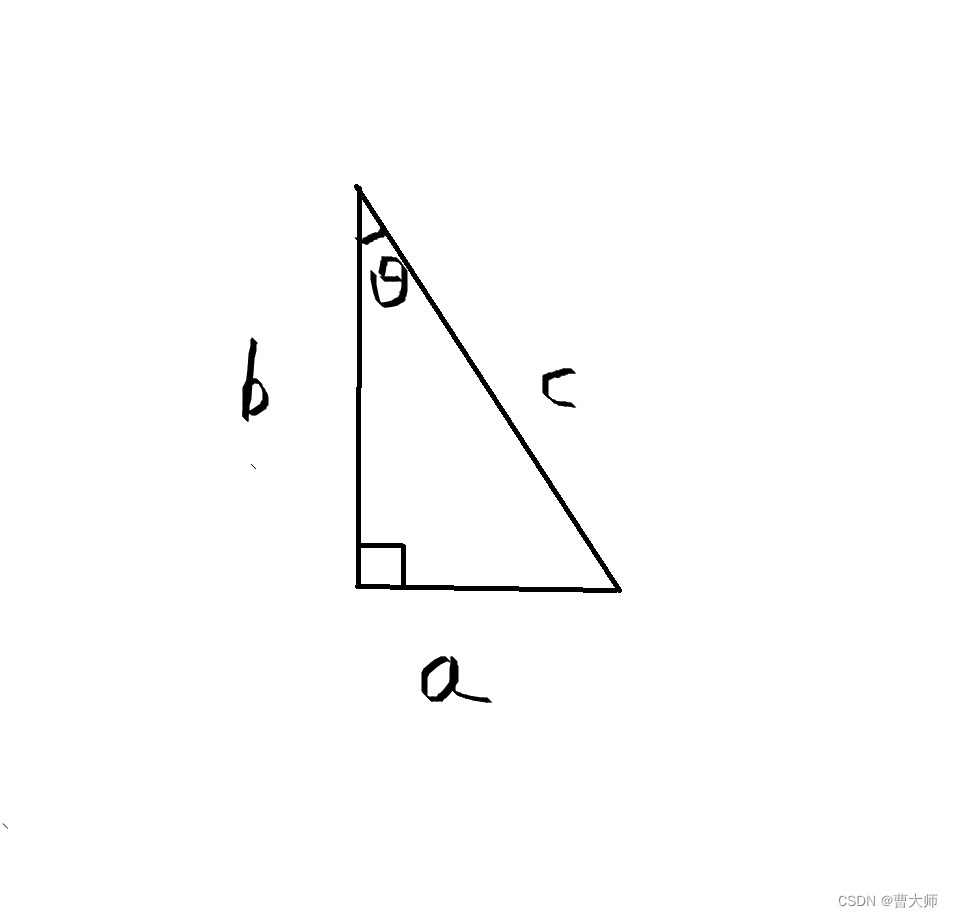
注意C++中三角函数使用的是弧度制(3.14) 。示例图中角为30度 sin(30/180*PI);//已知角度,求正弦cos(30/180*PI);//已知角度,求余弦tan(30/180*PI);//已知角度,求正切asin(a/c);//已知正弦值,求弧度acos(b/c);//已知余弦值,求弧度atan(a/b);//已知正切值,求弧度//如果要通过角度和边之间的关系求解,
C语言反三角函数编程:深度解析与实战指南
C语言反三角函数编程:深度解析与实战指南 在C语言的数学库中,反三角函数占据着举足轻重的地位。这些函数为我们提供了一种从三角函数值反推角度的方法,对于解决各种实际问题具有重要意义。本文将从四个方面、五个方面、六个方面和七个方面,对C语言中的反三角函数编程进行深度解析和实战指导。 四个方面:反三角函数的数学基础与C语言实现 反三角函数,包括反正弦(asin)、反余弦(www.szyg98.co
三角函数--char4
编制三角函数表: 要求在main()函数中调用show_sin_table(min_angle, max_angle),显示角度值为min_angle到max_angle之间的所有角度(间隔为1度)的正弦值。要求不能用数学库函数,将项目6中的mysin函数拷贝到这个程序中,用于计算sin值。例如show_sin_table(0, 90)可以显示出所有0到90度的正弦值。为取得更好的效果,可以考虑
高中数学:三角函数之考点精华-单调性问题
一、解题方法 1、换元 2、画图 3、反向求解 参考:整体换元法 二、练习 例题1 解析: 这一题,比较简单,是标准的换元法应用题。 这里稍微注意下第二小问的对称中心,因为,B=1,所以,对称中心的y=1 单调区间求解时,要注意复合函数的单调性口诀:同增异减 例题2 解析: 这一题较难 题目直接给出了我们增区间,所以,这个增区间必须是整体换元后增区间的子集。 从而,得出两个不等
数学分析复习:三角函数的周期性
文章目录 三角函数的周期性 本篇文章适合个人复习翻阅,不建议新手入门使用 三角函数的周期性 本节的主题是研究三角函数的周期性,我们之前已经解析地定义三角函数为 cos x = ∑ k = 0 ∞ ( − 1 ) k x 2 k ( 2 k ) ! , sin x = ∑ k = 0 ∞ ( − 1 ) k x 2 k + 1 ( 2 k + 1 ) ! \cos
高中数学:三角函数-基础知识
一、任意角 顺时针旋转是负值角 逆时针旋转式正值角 一个角对应一个终边 一个终边对应无数个角 x+k*360 例题 二、弧度制 弧长与半径的比值,就是角度 常见角度与弧度的对应关系 例题 三、弧长与扇形面积公式 注意:弧度制下的扇形面积公式,可以类比成三角形面积公式记忆 例题1 例题2 四、总结 要记住的核心公式 1、π=180° 2、α=l/r 3
勾股定理、三角函数、弧度在游戏中的运用
勾股定理 若知道直角三角形的任意两条边长,则可以求出第三条边的长度。 公式 :a²+b²=c² 这里的c一定是斜边 例1: 求斜边 解 : 3²+4²=c² c = 9 + 16 C = 25 例2: 求直角边 解: a²+4²=6² a² = 36 - 16 a = 20 三角函数 sinx = 对边/斜边 即 :a / c
【C#】C#踩坑三角函数之uvw平台
背景 最近再弄一个uvw平台,uvw平台厂商会提供一个公式里面用到了三角函数: 踩坑记录 一开始,我以为Math.Cos参数是度数,所以怎么算都不对! 一度怀疑C#的Math库。 后面才意识到,这个参数会不会是弧度?结果改成弧度就对了!!!! double θX1 = Ts(315);double θX2 = Ts(135);double θY = Ts(225);doub
洛谷刷题 | P1888 三角函数
三角函数 题目描述 输入一组勾股数 a , b , c ( a ≠ b ≠ c ) a,b,c(a\neq b\neq c) a,b,c(a=b=c),用分数格式输出其较小锐角的正弦值。(要求约分。) 输入格式 一行,包含三个正整数,即勾股数 a , b , c a,b,c a,b,c(无大小顺序)。 输出格式 一行,包含一个分数,即较小锐角的正弦值 样例 #1 样例输入
三角函数柔性加减速算法
公式推导 三段速度公式为 { v ( t ) = ( v s + v m ) / 2 − ( v m − v s ) c o s t ′ / 2 t ′ = ( t / t 1 ) π ( 1 ) v ( t ) = v m v ( t ) = ( v e + v m ) / 2 − ( v e − v m ) c o s t ′ / 2 t ′ = ( t / t 2 ) π t
数学分析(一)-实数集与函数3-函数概念6-初等函数4-三角函数6:arccotx【cotx的反函数】【减函数】【定义域:(-∞,+∞);值域:(0,π)】【arccot0=π/4】
高中数学,三角函数的图像与性质 系统化,轻快学习高中数学三角函数的图像、性质及其变换必备知识 精准狠——三角函数图像及其性质 三角函数与反三角函数(图像)
【高等数学】不常见的三角函数与反三角函数
余切函数( y = cot x y=\cot x y=cotx) 基本关系: cot x = 1 tan x = cos x sin x \cot x=\dfrac{1}{\tan x}=\dfrac{\cos x}{\sin x} cotx=tanx1=sinxcosx图像: 反余切函数( y = a r c c o t x \newcommand{\arccot}{\
第13周报告3:编制一个三角函数表
任务3:(函数的嵌套)编制一个三角函数表,要求在main()函数中调用show_sin_table(min_angle, max_angle),显示角度值为min_angle到max_angle之间的所有角度(间隔为1度)的正弦值。要求不能用数学库函数,将任务2中的mysin函数拷贝到这个程序中,用于计算sin值。例如show_sin_table(0, 90)可以显示出所有0到90度的正弦值。为取
c语言 拟合三角函数,使用Tensor拟合三角函数
numpy是一个很不错的库,但是在如今需要大量计算的深度学习中则显得力不从心。而pytorch所提供的张量Tensor能够很好的利用GPU的计算单元,在复杂的计算任务中能达到比GPU高几十甚至上千的算力。 对于Tensor,pytorch提供了许多方便的操作使其能进行科学计算。需要注意的是,使用GPU计算时要指定相应的设备。这里将使用tensor将三次多项式拟合为三角函数,话不多说,贴代码: i
AI-数学-高中-25-三角函数一图像解决三角函数不等式
原作者视频:【三角函数】【考点精华】1图像解决三角函数不等式问题(基础)_哔哩哔哩_bilibili 1.三角函数图像法; 2.不好画图像时:任意角的三角函数图像,在象限中比较,在4个象限中寻找角度的关系。 示例1: 示例2-2: 示例2-3:
科研踩坑:角度制三角函数求导要乘上π/180
写在前面 用MATLAB作图,查看其曲线和求导曲线是否和教材相一致,其中用了sin求导(角度制),以一个函数为例: y = C s i n d ( x ) y=\frac{C}{sind(x)} y=sind(x)C (sind(x)是以角度为单位后同),然后对它进行求导: d y d x = − C ⋅ c o s d ( x ) ( s i n d ( x ) ) 2 = − y
HLS 三角函数报错:undefined reference to ‘cordic_apfixed::circ_table_arctan_128‘
最近在通过HLS实现一些算法,其中用到了hls::cos函数,写完代码编译报错: ../Vitis_HLS/hls_cordic_apfixed.h:229: undefined reference to `cordic_apfixed::circ_table_arctan_128'build/xf_computePhaseMap_accel.o: In function `void cord
AI-数学-高中-23-三角函数的平移与伸缩
原作者视频:三角函数】11三角函数的平移伸缩(易)_哔哩哔哩_bilibili 左加右减:针对函数中的x变化,上加下减:针对函数f(x)变化。 示例1: 示例2: 示例3