科研踩坑：角度制三角函数求导要乘上π/180

本文主要是介绍科研踩坑：角度制三角函数求导要乘上π/180，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

写在前面

用MATLAB作图，查看其曲线和求导曲线是否和教材相一致，其中用了sin求导（角度制），以一个函数为例：

$y=\frac{C}{sind(x)}$

(sind(x)是以角度为单位后同)，然后对它进行求导：

$\frac{dy}{dx}=-\frac{C\cdot cosd(x)}{(sind(x){)}^2}=-\frac{y\cdot cosd(x)}{sind(x)}=-y\cdot cotd(x)$

$y=\frac{1}{sind(x)}$是单调递减函数，教材的图应该是对他进行了取绝对值的操作(要不原来是个负数)，也即：

$|\frac{dy}{dx}|=y\cdot cotd(x)$

编写下面的代码

clear 
close all
pm_theta_half=8:0.1:28;
pm_lambda_B0=1.9;
pm_constant=0.2644;
pm_lambda_B = pm_constant./sind(pm_theta_half);
dif_pm_lambda_theta_num=abs((diff(pm_lambda_B))./(diff(pm_theta_half)));
dif_pm_lambda_theta_cal=pm_lambda_B.*cotd(pm_theta_half);
colororder({'[0.2,0.5,0.7]','[0.17 0.31 0.16]'})
yyaxis left
plot(pm_theta_half,pm_lambda_B,...'LineWidth',3, ...'Color',[0.2,0.5,0.7]);ylabel('Bragg wavelength, \mum','FontSize',14);yyaxis right
plot(pm_theta_half(1,1:end-1),dif_pm_lambda_theta_num, ...'-.',...    'LineWidth',3, ..."Color",[0.17 0.31 0.16])
hold on;
scatter(pm_theta_half,dif_pm_lambda_theta_cal);
xlabel('Angle, \theta/2, degrees','FontSize',14)
ylabel('\Delta \lambda_b/degree \mum/deg','FontSize',14);
xaxis(8,28);
xticks(linspace(8,28,11))
ax = gca;
ax.FontSize = 14;

但是发现用离散求导和实际求导差很大，(绿色画圈的是求导计算式的值（不符合实际，范围和教材的图差别很大），点划线是离散求导的值（符合实际，范围和教材的图大致一样）)。

利用MATLAB自带的diff函数进行求解，终于找到了问题的所在！

syms x C
f=C/sind(x);
df1=diff(f,x,1)

经过求解如下：

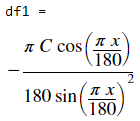
角度制的三角函数求导时要化成弧度制再进行求导！（国际单位rad！！！）我们再进行一次求导：

$\frac{dy}{dx}=\frac{d(\frac{C}{sind(x)})}{dx}=\frac{\frac{C}{sin(\pi \cdot x/180)}}{dx}=-\frac{C\cdot cos(\pi \cdot x/180)}{(sin(\pi \cdot x/180){)}^2}\cdot \frac{\pi }{180}=-\frac{y\cdot cos(\pi \cdot x/180)}{sin(\pi \cdot x/180)}\cdot \frac{\pi }{180}=-y\cdot cot(\frac{\pi \cdot x}{180})\cdot \frac{\pi }{180}=-y\cdot cotd(x)\cdot \frac{\pi }{180}$

可以看出角度制的三角函数求导要乘上π/180 !
修改代码中求导的那一项（第8行）如下：

dif_pm_lambda_theta_cal=pm_lambda_B.*cotd(pm_theta_half)*pi/180;

这样图就对应上了！

这篇关于科研踩坑：角度制三角函数求导要乘上π/180的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---