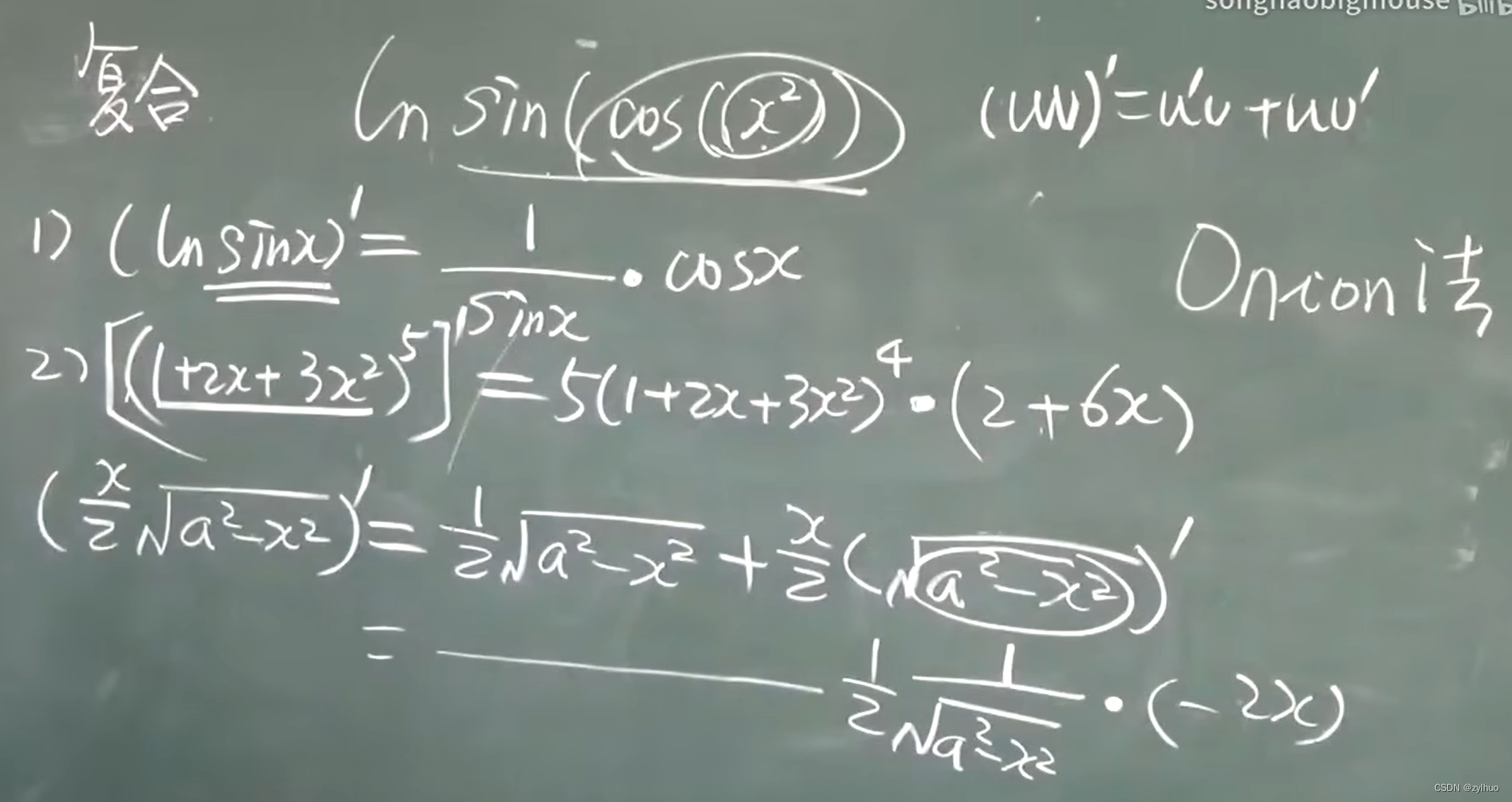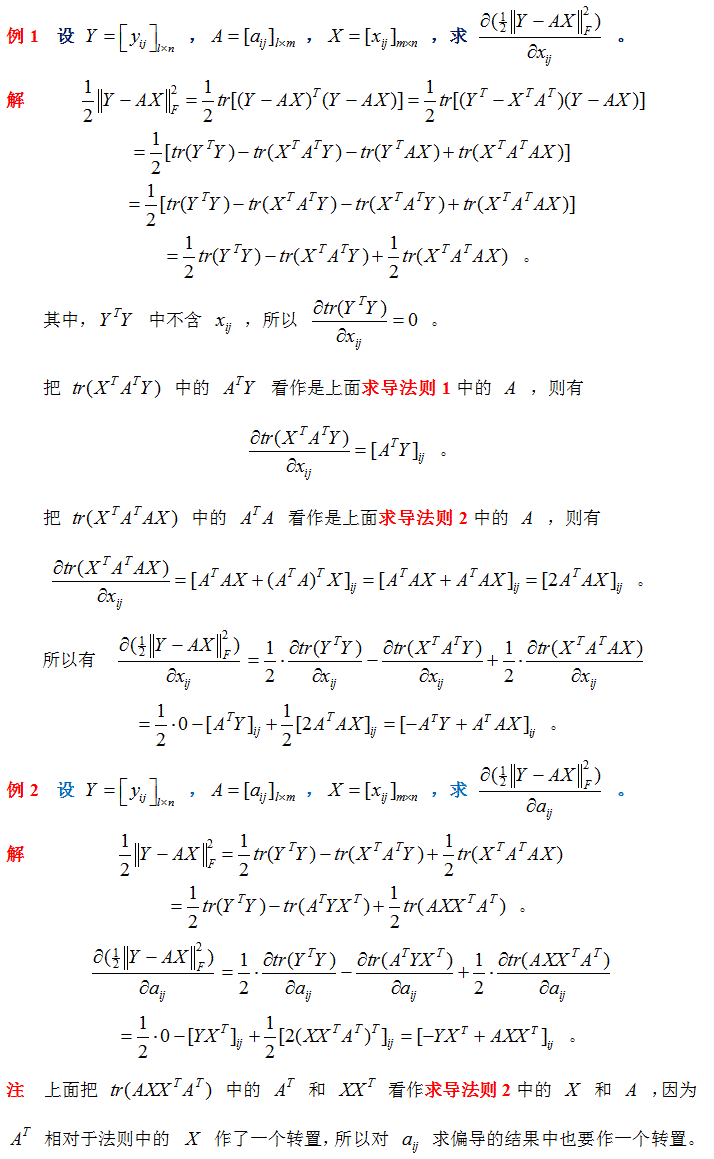求导专题

PyTorch 的自动求导与计算图

在深度学习中，模型的训练过程本质上是通过梯度下降算法不断优化损失函数。为了高效地计算梯度，PyTorch 提供了强大的自动求导机制，这一机制依赖于“计算图”（Computational Graph）的概念。 1. 什么是计算图？计算图是一种有向无环图（DAG），其中每个节点表示操作或变量，边表示数据的流动。简单来说，计算图是一个将复杂计算分解为一系列基本操作的图表。每个节点（通常称为“张量”

矩阵求导术（上）

矩阵求导术（上） - 知乎这篇博客的转载备份，希望大家去原博主那看，那边清晰明确一点。需要一点高数和线代的知识基本就能看懂，原博主讲的是真好。

矩阵的迹以及迹对矩阵求导

ref： https://blog.csdn.net/u012421852/article/details/79594933 矩阵的迹概念矩阵的迹就是矩阵的主对角线上所有元素的和。矩阵A的迹，记作tr(A)，可知tra(A)=∑aii，1<=i<=n。定理：tr(AB) = tr(BA) 证明定理：tr(ABC) = tr(CAB) =

NLP入门——复杂函数建模与链式求导

复杂函数建模前面我们研究的梯度下降法分类，是简单的对每类中每个子词的分数进行求和，统计分数最大的类别并不断调整分数来提高准确率。我们可以修改函数模型，用更加复杂的函数代替sum()，来达到更好的学习效果。 def compute_instance(model, lin):rs = {}_max_score, _max_class = -inf, Nonefor _class, v in m

Deep learning学习笔记(1)：CNN的反向求导及练习

转自：http://www.cnblogs.com/tornadomeet/p/3468450.html 　　前言：　　CNN作为DL中最成功的模型之一，有必要对其更进一步研究它。虽然在前面的博文Stacked CNN简单介绍中有大概介绍过CNN的使用，不过那是有个前提的：CNN中的参数必须已提前学习好。而本文的主要目的是介绍CNN参数在使用bp算法时该怎么训练，毕竟CNN中有卷积层和

概率论中两种特殊的 E(x) 计算方法：先求积分再求导，或者先求导再求积分

为了求解某个函数 ( E(x) )，可以使用两种方法：先求积分再求导，或者先求导再求积分。这里我们以数列求和公式为例，分别介绍这两种方法。 1. 先求积分再求导假设我们有一个函数 ( f(x) ) 的级数展开： E ( x ) = ∑ n = 1 ∞ a n x n E(x) = \sum_{n=1}^{\infty} a_n x^n E(x)=n=1∑∞anxn 我们可以通过对

概率论中，积分和再求导的计算方法

为了求解级数 1 + 2 2 q + 3 2 q 2 + … 1 + 2^2q + 3^2q^2 + \ldots 1+22q+32q2+… 的和，可以使用积分再求导的方法。我们考虑如下步骤： 1. 定义函数并进行积分我们先定义一个函数 S ( q ) S(q) S(q)： S ( q ) = ∑ n = 1 ∞ n 2 q n − 1 S(q) = \sum_{n=1}^{\inf

2024河南商丘ICPC Problem B. 表达式求导

题目描述给定一个合法的函数表达式f(x)，请你求出y=f(x)在a处的导数值，输入保证此处导数值一定存在，答案四舍五入保留两位小数。该函数表达式被称为合法，即满足以下要求： 1. x一定合法。 2. 如果表达式A合法，表达式BBB合法，那么A+B，A−B一定合法。 3. 如果表达式A合法，那么ln(A)ln(A)ln(A)也合法。输入描述本题有多组数据。第一行输入整数T(1

Pytorch学习笔记_2_Autograd自动求导机制

Autograd 自动求导机制 PyTorch 中所有神经网络的核心是 autograd 包。 autograd 包为张量上的所有操作提供了自动求导。它是一个在运行时定义的框架，可以通过代码的运行来决定反向传播的过程，并且每次迭代可以是不同的。通过一些示例来了解 Tensor 张量 torch.tensor是这个包的核心类。设置.requires_grad为True，会追踪所有对于

理解导数（x^n求导后nx^n-1）

以下都是为了方便理解微小量是 t M(x)是一个函数 M 在 x 处的斜率 = M 在 x 处的导数 = 垂直距离平移距离 = M ( x + t ) − M ( x ) ( x + t ) − x M在x处的斜率 = M在x处的导数= \dfrac{垂直距离}{平移距离} =\dfrac{M\left( x+t\right) -M\left( x\right) }{(x + t)

AI算法-高数3-导数-求导法则

P16 2.2 求导法则，宋浩老师：2.2 求导法则_哔哩哔哩_bilibili 反函数求导法则：复合函数求导：剥洋葱法。

漫步微积分八——多项式求导

微分学有其自身的独特性和重要性，已被应用到物理、生物和社会科学中。它能够快速渗入到应用中，并得到问题的核心。然而，从整体效率的角度看，它的具体内容推迟一下，我们先花一点时间学习如何快速而准确的求导。我们已经知道，对函数求导的过程称作微分。这个过程直接依赖于导数的极限定义， f ′ ( x ) = lim ⁡ Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x , f&#x

用SymPy简化神经网络的求导

神经网络模型这里不重点介绍神经网络模型，这里有神经网络比较简洁的介绍和推导。[机器学习] Coursera ML笔记 SymPy(符号计算框架)的安装我的系统为Ubuntu 14 安装比较简单：sudo apt-get install python-sympy【全部小写，csdn自动变成大写了◔ ‸◔?】求导为了简化叙述这里不用求和符号，w，b，x均为矩阵形式。在python终

计算图：深度学习中的链式求导与反向传播引擎

在深度学习的世界中，计算图扮演着至关重要的角色。它不仅是数学计算的图形化表示，更是链式求导与反向传播算法的核心。本文将深入探讨计算图的基本概念、与链式求导的紧密关系及其在反向传播中的应用，旨在为读者提供一个全面而深入的理解。计算图的基本概念计算图（Computational Graph）是一种用于描述数学计算过程的图形模型。在计算图中，节点代表数学运算或变量，边代表运算结果之间的依赖关

矩阵-向量求导法则

复杂矩阵问题求导方法：可以从小到大，从scalar到vector再到matrix。 x is a column vector, A is a matrix $d(A*x)/dx=A$ $d(x^T*A)/dx^T=A$ $d(x^T*A)/dx=A^T$ $d(x^T*A*x)/dx=x^T(A^T+A)$ pr

矩阵、向量的求导

在网上看到有人贴了如下求导公式： Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 于是把以前学过的矩阵求导部分整理一下： 1. 矩阵Y对标量x求导：相当于每个元素求导数后

矩阵的范数求导

转自：http://blog.csdn.net/chlele0105/article/details/21081917

logistic回归梯度下降的求导过程

logistic回归梯度下降的求导过程，记录一下

深度学习-自动求导

目录向量链式法则标量链式法则拓展到向量例题1例题2 符号求导数值求导自动求导计算图自动求导的两种模式链式法则正向累积（从x出发）反向累积（反向传递--先计算最终的函数即y）反向累积总结自动求导计算y关于x的梯度，使用requires_grad(True)计算y 通过调用反向传播函数来自动计算y关于x每个分量的梯度PyTorch会累积梯度，使用zero_()函数清除梯度批量中每个样本单

计算图中反向传播求导权重矩阵需要转置的说明

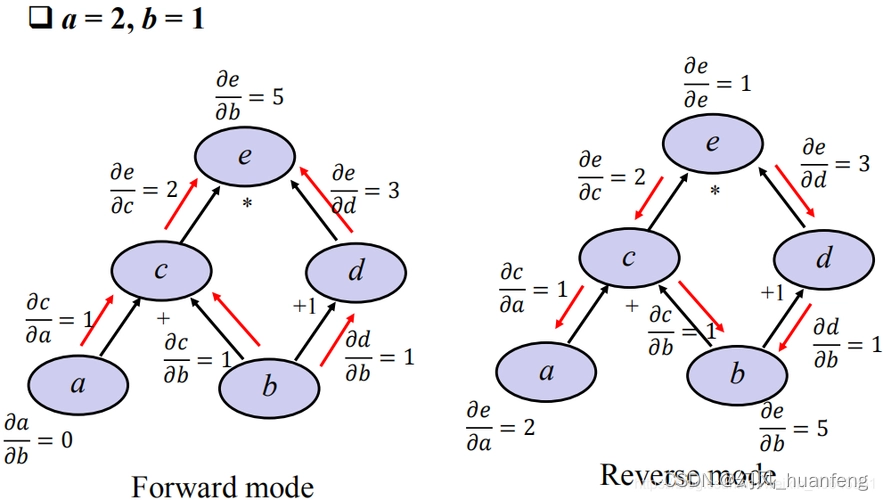
在计算图中，基于链式法则的计算图反向求导是模型训练的关键算法，下面用图例说明为什么反向传播的时候，权重矩阵需要转置按着图中箭头方向“从左向右进行计算”称为正向传播,即从计算图的出发点到结束点的传播, “从右往左计算”称为反向传播. 另一个例子: 当反向传播进来的是误差对上一层的导数时，反向传播矩阵使用正向传播矩阵的转置. 结束！

矩阵间的求导

最近由于需要手推一些最优化函数的求解公式，因此整理了一下各种矩阵间的求导法则，以方便理解相关库的代码或者自己动手代码实现。二范数类的矩阵求导形如 E = ∥ P ∥ 2 E = \left \| P \right \|^{2} E=∥P∥2 则有 σ E σ P = 2 P \frac{\sigma E}{\sigma P} = 2P σPσE=2P形如 E = ∥ P − Q ∥

收藏 | 神经网络的 5 种常见求导，附详细的公式过程

来源：机器学习与生成对抗网络本文约1800字，建议阅读5分钟本文为你介绍5种常见求导的详细过程！ 01 derivative of softmax 1.1 derivative of softmax 一般来说，分类模型的最后一层都是softmax层，假设我们有一个分类问题，那对应的softmax层结构如下图所示（一般认为输出的结果即为输入属于第i类的概率）：假设给定训练集

一个行列式求导

一个行列式求导公式 d ∣ A ∣ d t = ∣ A ∣ t r ( A − 1 ∗ d A d t ) , A ∈ R n × n \frac{d|A|}{dt} = |A|tr(A^{-1}*\frac{dA}{dt}),\ A\in R^{n \times n} dtd∣A∣=∣A∣tr(A−1∗dtdA), A∈Rn×n 证明如下首先我们有 ∣ A ( a i j +

pytorch教程之自动求导机制(AUTOGRAD)-从梯度和Jacobian矩阵讲起

文章目录 1. 梯度和Jacobian矩阵2. pytorch求变量导数的过程 1. 梯度和Jacobian矩阵设 f ( x ) ∈ R 1 f(x)\in R^1 f(x)∈R1是关于向量 x ∈ R n x\in R^n x∈Rn的函数，则它关于 x x x的导数定义为： d f ( x ) d x : = [ ∂ f ( x ) ∂ x i ] ∈ R n (1-

深度学习（自动求导）

介绍：深度学习是一种机器学习方法，其使用神经网络模型来进行学习和预测。自动求导是深度学习中的一项重要技术，用于计算神经网络中各个参数对损失函数的偏导数。在深度学习中，我们通常使用一个损失函数来衡量模型的预测结果与真实值之间的差异。然后，我们通过调整神经网络中的参数，以最小化损失函数，从而改善模型的预测能力。自动求导是指计算某个函数的导数时，由计算机自动完成的过程。在深度学习中，我们需要计

CNN的反向求导及练习

http://www.cnblogs.com/tornadomeet/p/3468450.html http://www.mamicode.com/info-detail-874778.html